Hostname: page-component-5cf477f64f-h6p2m Total loading time: 0 Render date: 2025-04-07T20:25:42.792Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behaviour in a doubly haptotactic cross-diffusion model for oncolytic virotherapy

Part of: Equations of mathematical physics and other areas of application Partial differential equations Physiological, cellular and medical topics Parabolic equations and systems

Published online by Cambridge University Press:  19 April 2022

Yifu Wang  and
Chi Xu
Yifu Wang
Affiliation:
School of Mathematics and Statistics, Beijing Institute of Technology, Beijing, 100081, P.R. China (wangyifu@bit.edu.cn; XuChi1993@126.com)
Chi Xu
Affiliation:
School of Mathematics and Statistics, Beijing Institute of Technology, Beijing, 100081, P.R. China (wangyifu@bit.edu.cn; XuChi1993@126.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper considers a model for oncolytic virotherapy given by the doubly haptotactic cross-diffusion system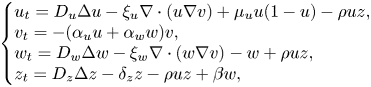

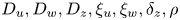\[ \left\{\begin{array}{@{}ll} u_t=D_u\Delta u-\xi_u\nabla\cdot(u\nabla v)+\mu_u u(1-u)-\rho uz,\\ v_t={-} (\alpha_u u+\alpha_w w)v,\\ w_t=D_w\Delta w-\xi_w\nabla\cdot(w\nabla v)- w+\rho uz,\\ z_t=D_z\Delta z-\delta_z z- \rho uz+\beta w, \end{array}\right. \]
with positive parameters $D_u,D_w,D_z,\xi _u,\xi _w,\delta _z,\rho$, $\alpha _u,\alpha _w,\mu _u,\beta$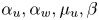. When posed under no-flux boundary conditions in a smoothly bounded domain $\Omega \subset {\mathbb {R}}^{2}$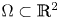, and along with initial conditions involving suitably regular data, the global existence of classical solution to this system was asserted in Tao and Winkler (2020, J. Differ. Equ. 268, 4973–4997). Based on the suitable quasi-Lyapunov functional, it is shown that when the virus replication rate $\beta <1$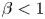, the global classical solution $(u,v,w,z)$ 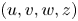is uniformly bounded and exponentially stabilizes to the constant equilibrium $(1, 0, 0, 0)$ 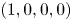in the topology $(L^{\infty }(\Omega ))^{4}$ 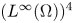as $t\rightarrow \infty$.

Keywords

HaptotaxisL log L-estimatesasymptotic behaviour

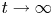MSC classification

Primary: 35K57: Reaction-diffusion equations
Secondary: 35B45: A priori estimates 35Q92: PDEs in connection with biology and other natural sciences 92C17: Cell movement (chemotaxis, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 3 , June 2023 , pp. 881 - 906
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alzahrani, T., Eftimie, R. and Trucu, D.. Multiscale modelling of cancer response to oncolytic viral therapy. Math. Bioci. 310 (2019), 76–95.Google ScholarPubMed
Anderson, A. R., Chaplain, M. A. J., Newman, E. L., Steele, R. J. C. and Thompson, A. M.. Mathematical modelling of tumour invasion and metastasis. J. Theor. Med. 2 (2000), 129–154.CrossRefGoogle Scholar
Cao, X.. Boundedness in a three-dimensional chemotaxis–haptotaxis model. Z. Angew. Math. Phys. 67 (2016), 11.CrossRefGoogle Scholar
Chen, Z.. Dampening effect of logistic source in a two-dimensional haptotaxis system with nonlinear zero-order interaction. J. Math. Anal. Appl. 492 (2020), 124435.CrossRefGoogle Scholar
Chaplain, M. A. J. and Lolas, G.. Mathematical modelling of cancer cell invasion of tissue: the role of the urokinase plasminogen activation system. Math. Mod. Meth. Appl. Sci. 18 (2005), 1685–1734.10.1142/S0218202505000947CrossRefGoogle Scholar
Fontelos, M. A., Friedman, A. and Hu, B.. Mathematical analysis of a model for the initiation of angiogenesis. SIAM J. Math. Anal. 33 (2002), 1330–1355.10.1137/S0036141001385046CrossRefGoogle Scholar
Fuest, M.. Global solutions near homogeneous steady states in a multi-dimensional population model with both predator-and prey-taxis. SIAM J. Math. Anal. 52 (2020), 5863–5891.10.1137/20M1344536CrossRefGoogle Scholar
Fukuhara, H., Ino, Y. and Todo, T.. Oncolytic virus therapy: a new era of cancer treatment at dawn. Cancer Sci. 107 (2016), 1373–1379.CrossRefGoogle ScholarPubMed
Gujar, S., Pol, J. G., Kim, Y., Lee, P. W. and Kroemer, G.. Antitumor benefits of antiviral immunity: an underappreciated aspect of oncolytic virotherapies. Trends Immunol. 39 (2018), 209–221.CrossRefGoogle ScholarPubMed
Ganly, I. and Kirn, D.. A phase I study of Onyx-015, an E1B-attenuated adenovirus, administered intratumorally to patients with recurrent head and neck cancer. Clin. Cancer Res. 6 (2000), 798–806.Google ScholarPubMed
Jin, C.. Global classical solutions and convergence to a mathematical model for cancer cells invasion and metastatic spread. J. Differ. Equ. 269 (2020), 3987–4021.10.1016/j.jde.2020.03.018CrossRefGoogle Scholar
Jin, H. Y. and Xiang, T.. Negligibility of haptotaxis effect in a chemotaxis–haptotaxis model. Math. Mod. Meth. Appl. Sci. 31 (2021), 1373–1417.CrossRefGoogle Scholar
Komarova, N. L.. Viral reproductive strategies: how can lytic viruses be evolutionarily competitive?. J. Theor. Biol. 249 (2007), 766–784.CrossRefGoogle ScholarPubMed
Li, Y. and Lankeit, J.. Boundedness in a chemotaxis–haptotaxis model with nonlinear diffusion. Nonlinearity 29 (2016), 1564–1595.10.1088/0951-7715/29/5/1564CrossRefGoogle Scholar
Li, J. and Wang, Y.. Boundedness in a haptotactic cross-diffusion system modeling oncolytic virotherapy. J. Differ. Equ. 270 (2021), 94–113.CrossRefGoogle Scholar
Nemunaitis, J. and Ganly, I.. Selective replication and oncolysis in p53 mutant tumors with ONYX-015, an E1B-55kD gene-deleted adenovirus, in patients with advanced head and neck cancer: a phase II trial. Cancer Res. 60 (2000), 6359–6366.Google ScholarPubMed
Pang, P. Y. H. and Wang, Y.. Global boundedness of solutions to a chemotaxis–haptotaxis model with tissue remodeling. Math. Models Methods Appl. Sci. 28 (2018), 2211–2235.CrossRefGoogle Scholar
Pang, P. Y. H. and Wang, Y.. Asymptotic behavior of solutions to a tumor angiogenesis model with chemotaxis–haptotaxis. Math. Models Methods Appl. Sci. 29 (2019), 1387–1412.CrossRefGoogle Scholar
Prüss, J., Zacher, R. and Schnaubelt, R.. Global asymptotic stability of equilibria in models for virus dynamics. Math. Model. Nat. Phenom. 3 (2008), 126–142.CrossRefGoogle Scholar
Ren, G. and Liu, B.. Global classical solvability in a three-dimensional haptotaxis system modeling oncolytic virotherapy. Math. Methods Appl. Sci. 44 (2021), 9275–9291.CrossRefGoogle Scholar
Stinner, C., Surulescu, C. and Winkler, M.. Global weak solutions in a PDE–ODE system modeling multiscale cancer cell invasion. SIAM J. Math. Anal. 46 (2014), 1969–2007.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Global classical solutions to a doubly haptotactic cross-diffusion system modeling oncolytic virotherapy. J. Differ. Equ. 268 (2020), 4973–4997.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Asymptotic stability of spatial homogeneity in a haptotaxis model for oncolytic virotherapy. Proc. R. Soc. Edinburgh Sect. A Math. 52 (2022), 81–101.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Critical mass for infinite-time blow-up in a haptotaxis system with nonlinear zero-order interaction. Discrete Contin. Dyn. Syst. A 41 (2021), 439–454.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. A critical virus production rate for efficiency of oncolytic virotherapy. European J. Appl. Math. 32 (2021), 301–316.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. A critical virus production rate for blow-up suppression in a haptotaxis model for oncolytic virotherapy. Nonlinear Anal. 198 (2020), 111870.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Large time behavior in a multidimensional chemotaxis–haptotaxis model with slow signal diffusion. SIAM J. Math. Anal. 47 (2015), 4229–4250.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Energy-type estimates and global solvability in a two-dimensional chemotaxis–haptotaxis model with remodeling of non-diffusible attractant. J. Differ. Equ. 257 (2014), 784–815.CrossRefGoogle Scholar
Walker, C. and Webb, G. F.. Global existence of classical solutions for a haptotaxis model. SIAM J. Math. Anal. 38 (2007), 1694–1713.10.1137/060655122CrossRefGoogle Scholar
Wang, Y.. Boundedness in the higher-dimensional chemotaxis–haptotaxis model with nonlinear diffusion. J. Differ. Equ. 260 (2016), 1975–1989.CrossRefGoogle Scholar
Winkler, M.. Aggregation vs. global diffusive behavior in the higher-dimensional Keller–Segel model. J. Differ. Equ. 12 (2010), 2889–2905.10.1016/j.jde.2010.02.008CrossRefGoogle Scholar
Zheng, J. and Ke, Y.. Large time behavior of solutions to a fully parabolic chemotaxis–haptotaxis model in $N$ dimensions. J. Differ. Equ. 266 (2019), 1969–2018.CrossRefGoogle Scholar
Zhigun, A., Surulescu, C. and Uatay, A.. Global existence for a degenerate haptotaxis model of cancer invasion. Z. Angew. Math. Phys. 67 (2016), 146.CrossRefGoogle Scholar