Published online by Cambridge University Press: 25 October 2016
We consider the following equation:
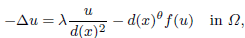
where d(x) = d(x, ∂Ω), θ > –2 and Ω is a half-space. The existence and non-existence of several kinds of positive solutions to this equation when 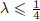 , f(u) = up (p > 1) and Ω is a bounded smooth domain were studied by Bandle, Moroz and Reichel in 2008. Here, we study exact the behaviour of positive solutions to this equation as d(x) → 0+ and d(x) → ∞, respectively, and the symmetry of positive solutions when
, f(u) = up (p > 1) and Ω is a bounded smooth domain were studied by Bandle, Moroz and Reichel in 2008. Here, we study exact the behaviour of positive solutions to this equation as d(x) → 0+ and d(x) → ∞, respectively, and the symmetry of positive solutions when 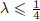 , Ω is a half-space and f(u) is a more general nonlinearity term than up . Under suitable conditions for f, we show that the equation has a unique positive solution W, which is a function of x 1 only, and W satisfies
, Ω is a half-space and f(u) is a more general nonlinearity term than up . Under suitable conditions for f, we show that the equation has a unique positive solution W, which is a function of x 1 only, and W satisfies