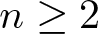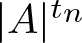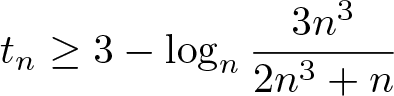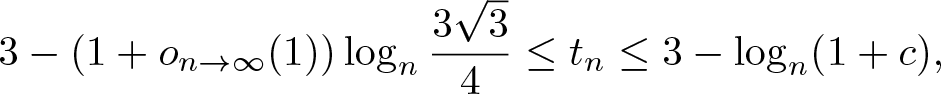1. Introduction
Let ![]() $A \subset G$ be a finite subset of an abelian group G. The additive energy E(A) of A is defined to be the number of additive quadruples in A:
$A \subset G$ be a finite subset of an abelian group G. The additive energy E(A) of A is defined to be the number of additive quadruples in A:
Trivially, we have ![]() $|A|^2 \leq E(A) \leq |A|^3$. A central theme in additive combinatorics is to understand the structure of those sets A whose additive energy E(A) is close to its trivial upper bound
$|A|^2 \leq E(A) \leq |A|^3$. A central theme in additive combinatorics is to understand the structure of those sets A whose additive energy E(A) is close to its trivial upper bound ![]() $|A|^3$. The famous Balog–Szemeredi–Gowers theorem and Freiman’s theorem are both results in this direction. See [Reference Tao and Vu15] for precise statements of these results and their proofs.
$|A|^3$. The famous Balog–Szemeredi–Gowers theorem and Freiman’s theorem are both results in this direction. See [Reference Tao and Vu15] for precise statements of these results and their proofs.
In this article, we study upper bounds for E(A) when A lies in certain subsets of ![]() $\mathbb{Z}^d$ for potentially large d. For a positive integer
$\mathbb{Z}^d$ for potentially large d. For a positive integer ![]() $n \geq 2$, define tn to be the smallest number such that
$n \geq 2$, define tn to be the smallest number such that ![]() $E(A) \leq |A|^{t_n}$ for all subsets
$E(A) \leq |A|^{t_n}$ for all subsets ![]() $A \subset \{0,1,\cdots,n-1\}^d$ and all positive integers d. One can calculate that
$A \subset \{0,1,\cdots,n-1\}^d$ and all positive integers d. One can calculate that
 \begin{equation*}
\begin{split}
E(\{0,1,\cdots,n-1\}) &= \sum_{s \in \mathbb{Z}} |\{(a,b): s=a+b, 0 \leq a,b\leq n-1\}|^2 \\
&= 1^2 + 2^2 + \cdots + n^2 + (n-1)^2 + \cdots + 1^2 = \frac{2n^3+n}{3}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
E(\{0,1,\cdots,n-1\}) &= \sum_{s \in \mathbb{Z}} |\{(a,b): s=a+b, 0 \leq a,b\leq n-1\}|^2 \\
&= 1^2 + 2^2 + \cdots + n^2 + (n-1)^2 + \cdots + 1^2 = \frac{2n^3+n}{3}
\end{split}
\end{equation*}and that
 \begin{equation*}
E(\{0,1,\cdots,n-1\}^d) = E(\{0,1,\cdots,n-1\})^d = \left(\frac{2n^3+n}{3}\right)^d.
\end{equation*}
\begin{equation*}
E(\{0,1,\cdots,n-1\}^d) = E(\{0,1,\cdots,n-1\})^d = \left(\frac{2n^3+n}{3}\right)^d.
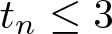
\end{equation*}Thus, we have the trivial bounds
 \begin{equation}
3 \geq t_n \geq \log_n \frac{2n^3+n}{3} = 3 - \log_n \frac{3n^3}{2n^3+n}.
\end{equation}
\begin{equation}
3 \geq t_n \geq \log_n \frac{2n^3+n}{3} = 3 - \log_n \frac{3n^3}{2n^3+n}.
\end{equation} It is known [Reference Kane and Tao9, theorem 7] that ![]() $t_2 = \log_26$ so that the lower bound in (1.1) for t 2 is sharp. For n = 3, it was proved in [Reference de Dios Pont, Greenfeld, Ivanisvili and Madrid6] that
$t_2 = \log_26$ so that the lower bound in (1.1) for t 2 is sharp. For n = 3, it was proved in [Reference de Dios Pont, Greenfeld, Ivanisvili and Madrid6] that
See [Reference de Dios Pont, Greenfeld, Ivanisvili and Madrid6, proposition 6] and its proof in [Reference de Dios Pont, Greenfeld, Ivanisvili and Madrid6, § 4.3]. In particular, this implies that the trivial lower bound ![]() $t_3 \geq \log_319 \approx 2.68$ in (1.1) is not sharp. Our main goal is to explore the behaviour of tn for large n.
$t_3 \geq \log_319 \approx 2.68$ in (1.1) is not sharp. Our main goal is to explore the behaviour of tn for large n.
Theorem 1.1 Let ![]() $n \geq 2$ be a positive integer. Then, for some absolute constant c > 0, we have
$n \geq 2$ be a positive integer. Then, for some absolute constant c > 0, we have
 \begin{equation*} 3 - (1+o_{n\rightarrow\infty}(1)) \log_n \frac{3\sqrt{3}}{4} \leq t_n \leq 3 - \log_n (1+c), \end{equation*}
\begin{equation*} 3 - (1+o_{n\rightarrow\infty}(1)) \log_n \frac{3\sqrt{3}}{4} \leq t_n \leq 3 - \log_n (1+c), \end{equation*} where ![]() $o_{n\rightarrow\infty}(1)$ denotes a quantity that tends to 0 as
$o_{n\rightarrow\infty}(1)$ denotes a quantity that tends to 0 as ![]() $n\rightarrow\infty$.
$n\rightarrow\infty$.
Unfortunately, the lower bound in theorem 1.1 is only meaningful for n sufficiently large. To complement that, we also prove the following result, which is valid for every ![]() $n \geq 3$.
$n \geq 3$.
Theorem 1.2 For any positive integer ![]() $n \geq 3$, we have
$n \geq 3$, we have
 \begin{equation*} t_n \gt \log_n E(\{0,1,\cdots,n-1\}) = \log_n \frac{2n^3+n}{3}. \end{equation*}
\begin{equation*} t_n \gt \log_n E(\{0,1,\cdots,n-1\}) = \log_n \frac{2n^3+n}{3}. \end{equation*} A key tool for the proof of both theorems comes from [Reference de Dios Pont, Greenfeld, Ivanisvili and Madrid6], which allows us to pass from studying subsets in ![]() $\mathbb{Z}^d$ to studying functions on
$\mathbb{Z}^d$ to studying functions on ![]() $\mathbb{Z}$. In § 2, we will describe this tool, outline the proofs, and make some remarks on further directions. The lower bound and the upper bound in theorem 1.1 will be proved in § 3 and § 4, respectively. Theorem 1.2 will be proved in § 5.
$\mathbb{Z}$. In § 2, we will describe this tool, outline the proofs, and make some remarks on further directions. The lower bound and the upper bound in theorem 1.1 will be proved in § 3 and § 4, respectively. Theorem 1.2 will be proved in § 5.
2. Proof outline
For a finitely supported function ![]() $f: \mathbb{Z} \rightarrow \mathbb{C}$, we define its Fourier transform
$f: \mathbb{Z} \rightarrow \mathbb{C}$, we define its Fourier transform  $\widehat{f}: \mathbb{R}/\mathbb{Z} \rightarrow \mathbb{C}$ by the formula
$\widehat{f}: \mathbb{R}/\mathbb{Z} \rightarrow \mathbb{C}$ by the formula
 \begin{equation*} \widehat{f}(\theta) = \sum_{a \in \mathbb{Z}} f(a) e(-a\theta), \end{equation*}
\begin{equation*} \widehat{f}(\theta) = \sum_{a \in \mathbb{Z}} f(a) e(-a\theta), \end{equation*} where ![]() $e(x) = e^{2\pi ix}$. For
$e(x) = e^{2\pi ix}$. For ![]() $p,q \geq 1$, the Lp-norm of
$p,q \geq 1$, the Lp-norm of ![]() $\widehat{f}$ and the
$\widehat{f}$ and the ![]() $\ell^q$-norm of f are defined by
$\ell^q$-norm of f are defined by
 \begin{equation*} \|\widehat{f}\|_p = \left(\int_0^1 |\widehat{f}(\theta)|^p \mathrm{d}\theta\right)^{1/p}, \ \ \|f\|_q = \left(\sum_{a \in \mathbb{Z}} |f(a)|^q\right)^{1/q}. \end{equation*}
\begin{equation*} \|\widehat{f}\|_p = \left(\int_0^1 |\widehat{f}(\theta)|^p \mathrm{d}\theta\right)^{1/p}, \ \ \|f\|_q = \left(\sum_{a \in \mathbb{Z}} |f(a)|^q\right)^{1/q}. \end{equation*} For two finitely supported functions ![]() $f, g: \mathbb{Z} \rightarrow \mathbb{C}$, their convolution
$f, g: \mathbb{Z} \rightarrow \mathbb{C}$, their convolution ![]() $f*g: \mathbb{Z}\rightarrow \mathbb{C}$ is defined by
$f*g: \mathbb{Z}\rightarrow \mathbb{C}$ is defined by
 \begin{equation*} f*g(s) = \sum_{a \in \mathbb{Z}} f(a) g(s-a). \end{equation*}
\begin{equation*} f*g(s) = \sum_{a \in \mathbb{Z}} f(a) g(s-a). \end{equation*}We have the identities
 \begin{equation*} \|\widehat{f}\|_4^4 = \|f*f\|_2^2 = \sum_{a, b, c \in \mathbb{Z}} f(a) f(b) \overline{f(c) f(a+b-c)}. \end{equation*}
\begin{equation*} \|\widehat{f}\|_4^4 = \|f*f\|_2^2 = \sum_{a, b, c \in \mathbb{Z}} f(a) f(b) \overline{f(c) f(a+b-c)}. \end{equation*} Thus, if ![]() $f = 1_A$ is the indicator function of a finite subset
$f = 1_A$ is the indicator function of a finite subset ![]() $A \subset \mathbb{Z}$, then
$A \subset \mathbb{Z}$, then
 \begin{equation*} E(A) = \|1_A*1_A\|_2^2 = \|\widehat{1_A}\|_4^4. \end{equation*}
\begin{equation*} E(A) = \|1_A*1_A\|_2^2 = \|\widehat{1_A}\|_4^4. \end{equation*} In § 3, we will also need to utilize Fourier transforms of functions on ![]() $\mathbb{R}$. For a piecewise continuous function
$\mathbb{R}$. For a piecewise continuous function ![]() $g: \mathbb{R}\rightarrow \mathbb{C}$, which has bounded support, we define its Fourier transform
$g: \mathbb{R}\rightarrow \mathbb{C}$, which has bounded support, we define its Fourier transform ![]() $\widehat{g}: \mathbb{R}\rightarrow \mathbb{C}$ by the formula
$\widehat{g}: \mathbb{R}\rightarrow \mathbb{C}$ by the formula
 \begin{equation*} \widehat{g}(y) = \int_{-\infty}^{+\infty} f(x) e(-xy) \mathrm{d} x. \end{equation*}
\begin{equation*} \widehat{g}(y) = \int_{-\infty}^{+\infty} f(x) e(-xy) \mathrm{d} x. \end{equation*} For two such functions ![]() $g,h$, we define their convolution
$g,h$, we define their convolution ![]() $g*h: \mathbb{R}\rightarrow \mathbb{C}$ by
$g*h: \mathbb{R}\rightarrow \mathbb{C}$ by
 \begin{equation*} g*h(z) = \int_{-\infty}^{+\infty} g(x) h(z-x) \mathrm{d} x. \end{equation*}
\begin{equation*} g*h(z) = \int_{-\infty}^{+\infty} g(x) h(z-x) \mathrm{d} x. \end{equation*}We have the identities
 \begin{equation*} \|\widehat{g}\|_4^4 = \|g*g\|_2^2 = \int\int\int g(x_1)g(x_2) \overline{g(x_3)g(x_1+x_2-x_3)} \mathrm{d} x_1 \mathrm{d} x_2 \mathrm{d} x_3. \end{equation*}
\begin{equation*} \|\widehat{g}\|_4^4 = \|g*g\|_2^2 = \int\int\int g(x_1)g(x_2) \overline{g(x_3)g(x_1+x_2-x_3)} \mathrm{d} x_1 \mathrm{d} x_2 \mathrm{d} x_3. \end{equation*}The machinery developed in [Reference de Dios Pont, Greenfeld, Ivanisvili and Madrid6, § 4] plays a key role in our proof. We summarize their result in the following proposition. Recall the definition of tn from § 1.
Proposition 2.1. Let ![]() $n \geq 2$ be a positive integer. We have
$n \geq 2$ be a positive integer. We have ![]() $t_n = 4/q_n$, where qn is the largest value of q such that the inequality
$t_n = 4/q_n$, where qn is the largest value of q such that the inequality  $\|\widehat{f}\|_4 \leq \|f\|_q$ holds for any function
$\|\widehat{f}\|_4 \leq \|f\|_q$ holds for any function ![]() $f: \mathbb{Z}\rightarrow \mathbb{R}$, which is supported on an interval of length n.
$f: \mathbb{Z}\rightarrow \mathbb{R}$, which is supported on an interval of length n.
Proof. This is essentially [Reference de Dios Pont, Greenfeld, Ivanisvili and Madrid6, proposition 21]. First, observe that by translation, we may restrict to those functions ![]() $f: \mathbb{Z}\rightarrow\mathbb{R}$ supported on
$f: \mathbb{Z}\rightarrow\mathbb{R}$ supported on ![]() $A = \{0,1,\cdots,n-1\}$ in the definition of qn. Then, in the language of [Reference de Dios Pont, Greenfeld, Ivanisvili and Madrid6, Definition 14], qn is the largest value of q such that
$A = \{0,1,\cdots,n-1\}$ in the definition of qn. Then, in the language of [Reference de Dios Pont, Greenfeld, Ivanisvili and Madrid6, Definition 14], qn is the largest value of q such that
where ![]() $\operatorname{DE}_{\ell^q\rightarrow L^4}(A)$ is the operator norm of the linear map
$\operatorname{DE}_{\ell^q\rightarrow L^4}(A)$ is the operator norm of the linear map ![]() $\ell^q(A) \rightarrow L^4(\mathbb{R}/\mathbb{Z})$ defined by the Fourier transform
$\ell^q(A) \rightarrow L^4(\mathbb{R}/\mathbb{Z})$ defined by the Fourier transform  $f \mapsto \widehat{f}$. By [Reference de Dios Pont, Greenfeld, Ivanisvili and Madrid6, proposition 21], (2.1) is equivalent to the statement that an inequality of the form
$f \mapsto \widehat{f}$. By [Reference de Dios Pont, Greenfeld, Ivanisvili and Madrid6, proposition 21], (2.1) is equivalent to the statement that an inequality of the form
holds for all subsets ![]() $X \subset A^d$ and
$X \subset A^d$ and ![]() $d \geq 1$. It follows that
$d \geq 1$. It follows that ![]() $t_n = 4/q_n$ by the definition of tn.
$t_n = 4/q_n$ by the definition of tn.
We remark that, by the Hausdorff–Young inequality, we always have
 \begin{equation*} \|\widehat{f}\|_4 \leq \|f\|_{4/3}. \end{equation*}
\begin{equation*} \|\widehat{f}\|_4 \leq \|f\|_{4/3}. \end{equation*} Hence, ![]() $q_n \geq 4/3$, and this recovers the trivial bound
$q_n \geq 4/3$, and this recovers the trivial bound ![]() $t_n \leq 3$. Moreover, the
$t_n \leq 3$. Moreover, the ![]() $\ell^{4/3}$-norm and the
$\ell^{4/3}$-norm and the ![]() $\ell^q$-norm for
$\ell^q$-norm for ![]() $q \gt 4/3$ are related by the inequalities
$q \gt 4/3$ are related by the inequalities
 \begin{equation}
\|f\|_q \leq \|f\|_{4/3} \leq |\operatorname{supp} f|^{3/4-1/q} \cdot \|f\|_q,
\end{equation}
\begin{equation}
\|f\|_q \leq \|f\|_{4/3} \leq |\operatorname{supp} f|^{3/4-1/q} \cdot \|f\|_q,
\end{equation} where ![]() $|\operatorname{supp}f|$ denotes the size of the support of f.
$|\operatorname{supp}f|$ denotes the size of the support of f.
In view of proposition 2.1, the lower and upper bounds in theorem 1.1 follow from propositions 2.2 and 2.3, respectively. In the remainder of this section, we discuss the main ideas behind the proofs of these two propositions and make some remarks about the quality of our bounds.
2.1. Lower bound for tn
In view of proposition 2.1, the lower bound for tn in theorem 1.1 is equivalent to the following proposition.
Proposition 2.2. Let ɛ > 0 and let n be sufficiently large in terms of ɛ. Let
 \begin{equation*} q = \frac{4}{3 - (1+\varepsilon)\log_n\frac{3\sqrt{3}}{4}}. \end{equation*}
\begin{equation*} q = \frac{4}{3 - (1+\varepsilon)\log_n\frac{3\sqrt{3}}{4}}. \end{equation*} There exists a function ![]() $f: \mathbb{Z}\rightarrow \mathbb{R}$, which is supported on an interval of length n such that
$f: \mathbb{Z}\rightarrow \mathbb{R}$, which is supported on an interval of length n such that  $\|\widehat{f}\|_4 \gt \|f\|_q$.
$\|\widehat{f}\|_4 \gt \|f\|_q$.
Our motivation for the construction of f in proposition 2.2 comes from the Babenko–Beckner inequality [Reference Babenko1, 2.3], a sharpened form of the Hausdorff–Young inequality for functions on ![]() $\mathbb{R}$ (and more generally on
$\mathbb{R}$ (and more generally on ![]() $\mathbb{R}^d$). It asserts that for any function
$\mathbb{R}^d$). It asserts that for any function ![]() $g: \mathbb{R}\rightarrow \mathbb{R}$, we have
$g: \mathbb{R}\rightarrow \mathbb{R}$, we have
 \begin{equation}
\|\widehat{g}\|_4 \leq \left(\frac{4\sqrt{3}}{9}\right)^{1/4} \|g\|_{4/3}.
\end{equation}
\begin{equation}
\|\widehat{g}\|_4 \leq \left(\frac{4\sqrt{3}}{9}\right)^{1/4} \|g\|_{4/3}.
\end{equation} Moreover, equality is achieved when g is the Gaussian function  $g(x) = e^{-x^2}$. In other words, Gaussian functions (and similarly their dilated versions) maximize the
$g(x) = e^{-x^2}$. In other words, Gaussian functions (and similarly their dilated versions) maximize the ![]() $\widehat{L}_4$-norm if we hold the
$\widehat{L}_4$-norm if we hold the ![]() $\ell^{4/3}$-norm fixed. If we take
$\ell^{4/3}$-norm fixed. If we take  $g(x) = e^{-x^2/A}$ with
$g(x) = e^{-x^2/A}$ with ![]() $A \approx n^2$ (so that g is essentially supported on an interval of length ≈ n), then direct computations show that
$A \approx n^2$ (so that g is essentially supported on an interval of length ≈ n), then direct computations show that
 \begin{equation*} \frac{\|g\|_{4/3}}{\|g\|_q} = c A^{\frac{1}{2}(\frac{3}{4}-\frac{1}{q})}, \end{equation*}
\begin{equation*} \frac{\|g\|_{4/3}}{\|g\|_q} = c A^{\frac{1}{2}(\frac{3}{4}-\frac{1}{q})}, \end{equation*} where c is an explicit constant depending on q and c ≈ 1 when ![]() $q \approx 4/3$. By our choice of A and q, we have
$q \approx 4/3$. By our choice of A and q, we have
 \begin{equation*} A^{\frac{1}{2}(\frac{3}{4}-\frac{1}{q})} \approx n^{\frac{3}{4}-\frac{1}{q}} = n^{\frac{1}{4}(1+\varepsilon)\log_n\frac{3\sqrt{3}}{4}} \approx \left(\frac{3\sqrt{3}}{4}+c\right)^{1/4} \end{equation*}
\begin{equation*} A^{\frac{1}{2}(\frac{3}{4}-\frac{1}{q})} \approx n^{\frac{3}{4}-\frac{1}{q}} = n^{\frac{1}{4}(1+\varepsilon)\log_n\frac{3\sqrt{3}}{4}} \approx \left(\frac{3\sqrt{3}}{4}+c\right)^{1/4} \end{equation*} for some constant ![]() $c=c(\varepsilon) \gt 0$. Hence, this function g(x) satisfies
$c=c(\varepsilon) \gt 0$. Hence, this function g(x) satisfies
 \begin{equation*} \|\widehat{g}\|_4 = \left(\frac{4\sqrt{3}}{9}\right)^{1/4} \|g\|_{4/3} \approx \left(\frac{4\sqrt{3}}{9}\right)^{1/4} \left(\frac{3\sqrt{3}}{4} + c\right)^{1/4}\|g\|_q \gt \|g\|_q. \end{equation*}
\begin{equation*} \|\widehat{g}\|_4 = \left(\frac{4\sqrt{3}}{9}\right)^{1/4} \|g\|_{4/3} \approx \left(\frac{4\sqrt{3}}{9}\right)^{1/4} \left(\frac{3\sqrt{3}}{4} + c\right)^{1/4}\|g\|_q \gt \|g\|_q. \end{equation*} If we define ![]() $f: \mathbb{Z}\rightarrow \mathbb{R}$ by sampling the values of g(x) at integral points, then we may expect that
$f: \mathbb{Z}\rightarrow \mathbb{R}$ by sampling the values of g(x) at integral points, then we may expect that
 \begin{equation*} \|\widehat{f}\|_4 \approx \|\widehat{g}\|_4, \ \ \|f\|_q \approx \|g\|_q, \end{equation*}
\begin{equation*} \|\widehat{f}\|_4 \approx \|\widehat{g}\|_4, \ \ \|f\|_q \approx \|g\|_q, \end{equation*} and thus, we should also have  $\|\widehat{f}\|_4 \gt \|f\|_q$. The details are worked out in § 3.
$\|\widehat{f}\|_4 \gt \|f\|_q$. The details are worked out in § 3.
2.2. Upper bound for tn
In view of proposition 2.1, the upper bound for tn in theorem 1.1 is equivalent to the following proposition.
Proposition 2.3. Let ![]() $n \geq 2$ be a positive integer and let
$n \geq 2$ be a positive integer and let ![]() $f: \mathbb{Z}\rightarrow \mathbb{R}$ be a function, which is supported on a set of size n. Let
$f: \mathbb{Z}\rightarrow \mathbb{R}$ be a function, which is supported on a set of size n. Let
 \begin{equation*} q = \frac{4}{3 - \log_n(1+c)} \end{equation*}
\begin{equation*} q = \frac{4}{3 - \log_n(1+c)} \end{equation*} for some sufficiently small absolute constant c > 0. Then,  $\|\widehat{f}\|_4 \leq \|f\|_q$.
$\|\widehat{f}\|_4 \leq \|f\|_q$.
The starting point of our proof of proposition 2.3 is the inequality
 \begin{equation}
\|\widehat{f}\|_4 \leq \|f\|_{4/3},
\end{equation}
\begin{equation}
\|\widehat{f}\|_4 \leq \|f\|_{4/3},
\end{equation}which follows from the Hausdorff–Young inequality or Young’s convolution inequality. By Hölder’s inequality (see (2.2)) and the definition of q, we have
 \begin{equation*} \|f\|_{4/3} \leq n^{3/4 - 1/q} \|f\|_q = (1+c)^{1/4} \|f\|_q. \end{equation*}
\begin{equation*} \|f\|_{4/3} \leq n^{3/4 - 1/q} \|f\|_q = (1+c)^{1/4} \|f\|_q. \end{equation*}Thus, the proof is already complete unless
 \begin{equation*} \|\widehat{f}\|_4 \geq (1+c)^{-1/4} \|f\|_{4/3}, \end{equation*}
\begin{equation*} \|\widehat{f}\|_4 \geq (1+c)^{-1/4} \|f\|_{4/3}, \end{equation*} and thus, a key part of our argument is to analyse when equality almost holds in (2.4). Note that equality holds exactly in (2.4) when f is supported on a singleton set. We prove in proposition 4.5 that if equality almost holds in (2.4), then f is well approximated by a function f 0, which is supported on a singleton set, up to an error g, which is small in ![]() $\ell^{4/3}$-norm. Clearly, the function f 0 satisfies
$\ell^{4/3}$-norm. Clearly, the function f 0 satisfies  $\|\widehat{f_0}\|_4 = \|f_0\|_q$. The remaining task is then to show that the error g can only swing the inequality in the desired direction. The details are carried out in § 4.
$\|\widehat{f_0}\|_4 = \|f_0\|_q$. The remaining task is then to show that the error g can only swing the inequality in the desired direction. The details are carried out in § 4.
We remark that proposition 4.5 is not new. In fact, it is a special case of [Reference Charalambides and Christ4, theorem 1.2] (see also [Reference Christ5] for an analogous result in Euclidean spaces) and of [Reference Eisner and Tao7, proposition 5.4]. As it turns out, our proof idea is the same as that in [Reference Eisner and Tao7], which, in turn, has its origin from [Reference Fournier8]. For completeness, we still give a self-contained proof of it in § 4.
2.3. Questions and speculations
Our proof of the lower bounds for tn is not constructive, which motivates the question of constructing explicit subsets of ![]() $\{0,1,\cdots,n-1\}^d$ with large additive energies.
$\{0,1,\cdots,n-1\}^d$ with large additive energies.
Questiona 2.4.
For sufficiently large n, construct a subset ![]() $A \subset \{0,1,\cdots,n-1\}^d$ for some d such that
$A \subset \{0,1,\cdots,n-1\}^d$ for some d such that ![]() $E(A) \geq |A|^t$, where
$E(A) \geq |A|^t$, where
 \begin{equation*} t = 3 - (1+o_{n\rightarrow\infty}(1)) \log_n \frac{3\sqrt{3}}{4}. \end{equation*}
\begin{equation*} t = 3 - (1+o_{n\rightarrow\infty}(1)) \log_n \frac{3\sqrt{3}}{4}. \end{equation*} A possible candidate for such a set A is the set of lattice points in a d-dimensional ball ![]() $B_d \subset \mathbb{R}^d$ (with an appropriate choice of d and an appropriate centre and radius). This choice is motivated by results in [Reference Shao12], which implies, roughly speaking, that such a set A maximizes the additive energy among all genuinely d-dimensional subsets of
$B_d \subset \mathbb{R}^d$ (with an appropriate choice of d and an appropriate centre and radius). This choice is motivated by results in [Reference Shao12], which implies, roughly speaking, that such a set A maximizes the additive energy among all genuinely d-dimensional subsets of ![]() $\mathbb{Z}^d$ of a given cardinality. Moreover,
$\mathbb{Z}^d$ of a given cardinality. Moreover, ![]() $E(A) \approx E(B_d)$, and it follows from the computations in [Reference Mazur11, § 3.1] that
$E(A) \approx E(B_d)$, and it follows from the computations in [Reference Mazur11, § 3.1] that
 \begin{equation*} E(B_d) = \left(\frac{4\sqrt{3}}{9} + o_{d\rightarrow\infty}(1)\right)^d |B_d|^3, \end{equation*}
\begin{equation*} E(B_d) = \left(\frac{4\sqrt{3}}{9} + o_{d\rightarrow\infty}(1)\right)^d |B_d|^3, \end{equation*} where ![]() $|B_d|$ denotes the Lebesgue measure of Bd.
$|B_d|$ denotes the Lebesgue measure of Bd.
Next we speculate the asymptotic behaviour of tn as ![]() $n\rightarrow\infty$. Note that if
$n\rightarrow\infty$. Note that if ![]() $g: \mathbb{R}\rightarrow \mathbb{R}$ is a (continuous) function supported on an interval of length n and
$g: \mathbb{R}\rightarrow \mathbb{R}$ is a (continuous) function supported on an interval of length n and
 \begin{equation*} q = \frac{4}{3-\log_n\frac{3\sqrt{3}}{4}}, \end{equation*}
\begin{equation*} q = \frac{4}{3-\log_n\frac{3\sqrt{3}}{4}}, \end{equation*}then
 \begin{equation*} \|\widehat{g}\|_4 \leq \left(\frac{4\sqrt{3}}{9}\right)^{1/4} \|g\|_{4/3} \leq \left(\frac{4\sqrt{3}}{9}\right)^{1/4} n^{3/4-1/q} \|g\|_q = \|g\|_q, \end{equation*}
\begin{equation*} \|\widehat{g}\|_4 \leq \left(\frac{4\sqrt{3}}{9}\right)^{1/4} \|g\|_{4/3} \leq \left(\frac{4\sqrt{3}}{9}\right)^{1/4} n^{3/4-1/q} \|g\|_q = \|g\|_q, \end{equation*}where the first inequality follows from the Babenko–Beckner inequality (2.3) and the second inequality follows from Hölder’s inequality (a continuous version of (2.2)). Based on this, it is perhaps reasonable to conjecture that a similar bound holds for discrete functions.
Conjecture 2.5.
Let ɛ > 0 and let n be sufficiently large in terms of ɛ. Let
 \begin{equation*} q = \frac{4}{3 - (1-\varepsilon)\log_n\frac{3\sqrt{3}}{4}}. \end{equation*}
\begin{equation*} q = \frac{4}{3 - (1-\varepsilon)\log_n\frac{3\sqrt{3}}{4}}. \end{equation*} Then, for any function ![]() $f: \mathbb{Z}\rightarrow \mathbb{R}$, which is supported on an interval of length n, we have
$f: \mathbb{Z}\rightarrow \mathbb{R}$, which is supported on an interval of length n, we have  $\|\widehat{f}\|_4 \leq \|f\|_q$.
$\|\widehat{f}\|_4 \leq \|f\|_q$.
In particular, the conjecture would imply that
 \begin{equation*} t_n = 3 - (1+o_{n\rightarrow\infty}(1)) \log_n \frac{3\sqrt{3}}{4}. \end{equation*}
\begin{equation*} t_n = 3 - (1+o_{n\rightarrow\infty}(1)) \log_n \frac{3\sqrt{3}}{4}. \end{equation*}So perhaps the lower bound in theorem 1.1 is sharp up to the error in o(1).
3. Lower bound for tn
In this section, we prove proposition 2.2. Throughout this section, let ɛ > 0 be small and let ![]() $n = 2k+1$ be sufficiently large in terms of ɛ. We will construct a function
$n = 2k+1$ be sufficiently large in terms of ɛ. We will construct a function ![]() $f: \mathbb{Z}\rightarrow \mathbb{R}$ supported on
$f: \mathbb{Z}\rightarrow \mathbb{R}$ supported on ![]() $\{-k,\cdots,k\}$ such that
$\{-k,\cdots,k\}$ such that  $\|\widehat{f}\|_4 \gt \|f\|_q$, where
$\|\widehat{f}\|_4 \gt \|f\|_q$, where
 \begin{equation*} q = \frac{4}{3-(1+\varepsilon) \log_n \frac{3\sqrt{3}}{4}}. \end{equation*}
\begin{equation*} q = \frac{4}{3-(1+\varepsilon) \log_n \frac{3\sqrt{3}}{4}}. \end{equation*} Define ![]() $g: \mathbb{R}\rightarrow \mathbb{R}$ by
$g: \mathbb{R}\rightarrow \mathbb{R}$ by ![]() $g(x) = \exp(-x^2/A)$, where
$g(x) = \exp(-x^2/A)$, where ![]() $A = k^{2-\varepsilon/10}$.
$A = k^{2-\varepsilon/10}$.
Lemma 3.1. We have ![]() $\|\widehat{g}\|_4 \geq (1+c\varepsilon)\|g\|_q$ for some absolute constant c > 0.
$\|\widehat{g}\|_4 \geq (1+c\varepsilon)\|g\|_q$ for some absolute constant c > 0.
Proof. One can compute that
 \begin{equation*} \widehat{g}(y) = (\pi A)^{1/2} e^{-\pi^2 A y^2}, \end{equation*}
\begin{equation*} \widehat{g}(y) = (\pi A)^{1/2} e^{-\pi^2 A y^2}, \end{equation*}and hence,
 \begin{equation*} \|\widehat{g}\|_4^4 = (\pi A)^2 \int_{-\infty}^{\infty} e^{-4\pi^2 A y^2} \mathrm{d} y = \frac{1}{2} (\pi A)^{3/2}. \end{equation*}
\begin{equation*} \|\widehat{g}\|_4^4 = (\pi A)^2 \int_{-\infty}^{\infty} e^{-4\pi^2 A y^2} \mathrm{d} y = \frac{1}{2} (\pi A)^{3/2}. \end{equation*}On the other hand, we have
 \begin{equation*} \|g\|_q^q = \int_{-\infty}^{\infty} e^{-qx^2/A} \mathrm{d} x = \left(\frac{\pi A}{q}\right)^{1/2}. \end{equation*}
\begin{equation*} \|g\|_q^q = \int_{-\infty}^{\infty} e^{-qx^2/A} \mathrm{d} x = \left(\frac{\pi A}{q}\right)^{1/2}. \end{equation*}It follows that
 \begin{equation*} \frac{\|\widehat{g}\|_4}{\|g\|_q} = \left(\frac{1}{4} q^{4/q} \pi^{3-4/q} A^{3-4/q}\right)^{1/8}. \end{equation*}
\begin{equation*} \frac{\|\widehat{g}\|_4}{\|g\|_q} = \left(\frac{1}{4} q^{4/q} \pi^{3-4/q} A^{3-4/q}\right)^{1/8}. \end{equation*}By our choice of A, we have
 \begin{align*} A^{3-4/q} & = \exp\left( \left(2-\frac{\varepsilon}{10}\right) (\log k) (1+\varepsilon)\log_n\frac{3\sqrt{3}}{4} \right) \\
& \geq \exp\left((2+\varepsilon)\log\frac{3\sqrt{3}}{4}\right) \geq (1+c\varepsilon) \frac{27}{16} \end{align*}
\begin{align*} A^{3-4/q} & = \exp\left( \left(2-\frac{\varepsilon}{10}\right) (\log k) (1+\varepsilon)\log_n\frac{3\sqrt{3}}{4} \right) \\
& \geq \exp\left((2+\varepsilon)\log\frac{3\sqrt{3}}{4}\right) \geq (1+c\varepsilon) \frac{27}{16} \end{align*} for some absolute constant c > 0. By choosing k to be sufficiently large in terms of ɛ, we may ensure that q is sufficiently close to ![]() $4/3$ so that
$4/3$ so that
 \begin{equation*} \frac{1}{4} q^{4/q} \pi^{3-4/q} \geq \left(1-\frac{c\varepsilon}{2}\right) \frac{1}{4} \left(\frac{4}{3}\right)^3 = \left(1-\frac{c\varepsilon}{2}\right) \frac{16}{27}. \end{equation*}
\begin{equation*} \frac{1}{4} q^{4/q} \pi^{3-4/q} \geq \left(1-\frac{c\varepsilon}{2}\right) \frac{1}{4} \left(\frac{4}{3}\right)^3 = \left(1-\frac{c\varepsilon}{2}\right) \frac{16}{27}. \end{equation*}Combining the two inequalities above, we conclude that
 \begin{equation*} \frac{\|\widehat{g}\|_4}{\|g\|_q} \geq \left[(1+c\varepsilon)\left(1-\frac{c\varepsilon}{2}\right)\right]^{1/8} \geq 1 + \frac{c\varepsilon}{100}. \end{equation*}
\begin{equation*} \frac{\|\widehat{g}\|_4}{\|g\|_q} \geq \left[(1+c\varepsilon)\left(1-\frac{c\varepsilon}{2}\right)\right]^{1/8} \geq 1 + \frac{c\varepsilon}{100}. \end{equation*} Now we truncate g to have bounded support. Set ![]() $M = \lfloor k^{1-\varepsilon/100}\rfloor$. Let
$M = \lfloor k^{1-\varepsilon/100}\rfloor$. Let ![]() $g_M: \mathbb{R}\rightarrow \mathbb{R}$ be the truncation of g defined by
$g_M: \mathbb{R}\rightarrow \mathbb{R}$ be the truncation of g defined by
 \begin{equation*} g_M(x) = \begin{cases} g(x) & \text{if } -M \leq x \lt M, \\ 0 & \text{otherwise.} \end{cases} \end{equation*}
\begin{equation*} g_M(x) = \begin{cases} g(x) & \text{if } -M \leq x \lt M, \\ 0 & \text{otherwise.} \end{cases} \end{equation*}Lemma 3.2. We have ![]() $\|\widehat{g_M}\|_4 \geq \|\widehat{g}\|_4 - \exp(-k^{\varepsilon/20})$ and
$\|\widehat{g_M}\|_4 \geq \|\widehat{g}\|_4 - \exp(-k^{\varepsilon/20})$ and ![]() $\|g_M\|_q \leq \|g\|_q$.
$\|g_M\|_q \leq \|g\|_q$.
Proof. The inequality ![]() $\|g_M\|_q \leq \|g\|_q$ follows trivially from the definition of gM. Concerning the L 4-norm of their Fourier transforms, we have by the triangle inequality, Hausdorff–Young inequality, and Hölder’s inequality that
$\|g_M\|_q \leq \|g\|_q$ follows trivially from the definition of gM. Concerning the L 4-norm of their Fourier transforms, we have by the triangle inequality, Hausdorff–Young inequality, and Hölder’s inequality that
 \begin{equation*} \|\widehat{g}\|_4 - \|\widehat{g_M}\|_4 \leq \|\widehat{g-g_M}\|_4 \leq \|g-g_M\|_{4/3} \leq \|g-g_M\|_{\infty}^{1/4} \|g-g_M\|_1^{3/4}. \end{equation*}
\begin{equation*} \|\widehat{g}\|_4 - \|\widehat{g_M}\|_4 \leq \|\widehat{g-g_M}\|_4 \leq \|g-g_M\|_{4/3} \leq \|g-g_M\|_{\infty}^{1/4} \|g-g_M\|_1^{3/4}. \end{equation*}Since
and
 \begin{equation*} \|g-g_M\|_1 \leq \|g\|_1 = \int_{-\infty}^{\infty} e^{-x^2/A} \mathrm{d} x = (\pi A)^{1/2} \ll k, \end{equation*}
\begin{equation*} \|g-g_M\|_1 \leq \|g\|_1 = \int_{-\infty}^{\infty} e^{-x^2/A} \mathrm{d} x = (\pi A)^{1/2} \ll k, \end{equation*}it follows that
 \begin{equation*} \|g-g_M\|_{\infty}^{1/4} \|g-g_M\|_1^{3/4} \leq \exp(-k^{\varepsilon/20}), \end{equation*}
\begin{equation*} \|g-g_M\|_{\infty}^{1/4} \|g-g_M\|_1^{3/4} \leq \exp(-k^{\varepsilon/20}), \end{equation*}once k is large enough in terms of ɛ.
Now we discretize gM. Define ![]() $f: \mathbb{Z} \rightarrow \mathbb{R}$ by
$f: \mathbb{Z} \rightarrow \mathbb{R}$ by ![]() $f(m) = g_M(m)$ for
$f(m) = g_M(m)$ for ![]() $m \in \mathbb{Z}$. Then, f is supported on
$m \in \mathbb{Z}$. Then, f is supported on ![]() $\{-M,\cdots,M\} \subset \{-k,\cdots,k\}$.
$\{-M,\cdots,M\} \subset \{-k,\cdots,k\}$.
Lemma 3.3. For ![]() $m \in \mathbb{Z}$, let
$m \in \mathbb{Z}$, let ![]() $I_m = [m, m+1)$. Then,
$I_m = [m, m+1)$. Then,
 \begin{equation*} \sup_{x \in I_m} |g_M(x) - f(m)| \ll k^{-1/2} f(m) \end{equation*}
\begin{equation*} \sup_{x \in I_m} |g_M(x) - f(m)| \ll k^{-1/2} f(m) \end{equation*} for every ![]() $m \in \mathbb{Z}$.
$m \in \mathbb{Z}$.
Proof. If ![]() $m \geq M$ or
$m \geq M$ or ![]() $m \leq -M-1$, then
$m \leq -M-1$, then ![]() $f(m) = 0$ and
$f(m) = 0$ and ![]() $g_M(x) = 0$ for every
$g_M(x) = 0$ for every ![]() $x \in I_m$, and hence, the conclusion holds trivially. Now assume that
$x \in I_m$, and hence, the conclusion holds trivially. Now assume that ![]() $m \in \{-M, \cdots, M-1\}$, so that
$m \in \{-M, \cdots, M-1\}$, so that ![]() $I_m \subset [-M, M)$, and thus,
$I_m \subset [-M, M)$, and thus, ![]() $g_M(x) = g(x)$ for
$g_M(x) = g(x)$ for ![]() $x \in I_m$. Hence, for
$x \in I_m$. Hence, for ![]() $x \in I_m$, we have
$x \in I_m$, we have
 \begin{align*} |g_M(x) - f(m)| & = |g(x) - g(m)| \leq \sup_{y \in [x,m]} |g'(y)| = \frac{2}{A} \sup_{y \in I_m} |yg(y)| \\
& \leq \frac{2}{A}(1+|m|) \sup_{y \in I_m} g(y). \end{align*}
\begin{align*} |g_M(x) - f(m)| & = |g(x) - g(m)| \leq \sup_{y \in [x,m]} |g'(y)| = \frac{2}{A} \sup_{y \in I_m} |yg(y)| \\
& \leq \frac{2}{A}(1+|m|) \sup_{y \in I_m} g(y). \end{align*}Since
it follows that
 \begin{equation*} |g_M(x) - f(m)| \ll \frac{M}{A} g(m) \ll k^{-1/2} g(m). \end{equation*}
\begin{equation*} |g_M(x) - f(m)| \ll \frac{M}{A} g(m) \ll k^{-1/2} g(m). \end{equation*}Lemma 3.4. We have  $\|\widehat{g_M}\|_4 \leq (1 + O(k^{-1/2})) \|\widehat{f}\|_4$ and
$\|\widehat{g_M}\|_4 \leq (1 + O(k^{-1/2})) \|\widehat{f}\|_4$ and  $\|g_M\|_q = (1 + O(k^{-1/2})) \|f\|_q$.
$\|g_M\|_q = (1 + O(k^{-1/2})) \|f\|_q$.
Proof. Note that
 \begin{equation*}
\begin{split}
\|\widehat{g_M}\|_4^4 &= \int\int\int g_M(x_1)g_M(x_2)g_M(x_3)g_M(x_1+x_2-x_3) \mathrm{d} x_1 \mathrm{d} x_2 \mathrm{d} x_3 \\
&= \sum_{a_1,a_2,a_3,a_4 \in \mathbb{Z}} \int\int\int g_M\vert_{I_{a_1}}(x_1) g_M\vert_{I_{a_2}}(x_2) g_M\vert_{I_{a_3}}(x_3) g_M\vert_{I_{a_4}}\\
& \quad \times (x_1+x_2-x_3) \mathrm{d} x_1 \mathrm{d} x_2 \mathrm{d} x_3.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\|\widehat{g_M}\|_4^4 &= \int\int\int g_M(x_1)g_M(x_2)g_M(x_3)g_M(x_1+x_2-x_3) \mathrm{d} x_1 \mathrm{d} x_2 \mathrm{d} x_3 \\
&= \sum_{a_1,a_2,a_3,a_4 \in \mathbb{Z}} \int\int\int g_M\vert_{I_{a_1}}(x_1) g_M\vert_{I_{a_2}}(x_2) g_M\vert_{I_{a_3}}(x_3) g_M\vert_{I_{a_4}}\\
& \quad \times (x_1+x_2-x_3) \mathrm{d} x_1 \mathrm{d} x_2 \mathrm{d} x_3.
\end{split}
\end{equation*}By lemma 3.3, we have
 \begin{equation*} g_M\vert_{I_a}(x) = (1+O(k^{-1/2})) f(a) 1_{I_a}(x) \end{equation*}
\begin{equation*} g_M\vert_{I_a}(x) = (1+O(k^{-1/2})) f(a) 1_{I_a}(x) \end{equation*} for any ![]() $a \in \mathbb{Z}$ and
$a \in \mathbb{Z}$ and ![]() $x \in \mathbb{R}$. Hence,
$x \in \mathbb{R}$. Hence,
 \begin{equation*}
\|\widehat{g_M}\|_4^4 = \left(1 + O(k^{-1/2})\right) \sum_{a_1,a_2,a_3,a_4 \in \mathbb{Z}} f(a_1) f(a_2) f(a_3) f(a_4) I(a_1,a_2,a_3,a_4),
\end{equation*}
\begin{equation*}
\|\widehat{g_M}\|_4^4 = \left(1 + O(k^{-1/2})\right) \sum_{a_1,a_2,a_3,a_4 \in \mathbb{Z}} f(a_1) f(a_2) f(a_3) f(a_4) I(a_1,a_2,a_3,a_4),
\end{equation*}where
 \begin{equation*}
I(a_1,a_2,a_3,a_4) = \int\int\int 1_{I_{a_1}}(x_1) 1_{I_{a_2}}(x_2) 1_{I_{a_3}}(x_3) 1_{I_{a_4}}(x_1+x_2-x_3) \mathrm{d} x_1 \mathrm{d} x_2 \mathrm{d} x_3.
\end{equation*}
\begin{equation*}
I(a_1,a_2,a_3,a_4) = \int\int\int 1_{I_{a_1}}(x_1) 1_{I_{a_2}}(x_2) 1_{I_{a_3}}(x_3) 1_{I_{a_4}}(x_1+x_2-x_3) \mathrm{d} x_1 \mathrm{d} x_2 \mathrm{d} x_3.
\end{equation*} By shifting the variables ![]() $x_1,x_2,x_3$ in the integral above, we see that
$x_1,x_2,x_3$ in the integral above, we see that
It follows that
 \begin{equation*} \|\widehat{g_M}\|_4^4 = \left(1 + O(k^{-1/2})\right) \sum_{a \in \mathbb{Z}} I(0,0,0,a) \sum_{\substack{a_1,a_2,a_3,a_4 \in \mathbb{Z} \\ a_3+a_4-a_1-a_2=a}} f(a_1) f(a_2) f(a_3) f(a_4) \end{equation*}
\begin{equation*} \|\widehat{g_M}\|_4^4 = \left(1 + O(k^{-1/2})\right) \sum_{a \in \mathbb{Z}} I(0,0,0,a) \sum_{\substack{a_1,a_2,a_3,a_4 \in \mathbb{Z} \\ a_3+a_4-a_1-a_2=a}} f(a_1) f(a_2) f(a_3) f(a_4) \end{equation*}By Fourier analysis, we have
 \begin{equation*}
\sum_{\substack{a_1,a_2,a_3,a_4 \in \mathbb{Z} \\ a_3+a_4-a_1-a_2=a}} f(a_1) f(a_2) f(a_3) f(a_4) = \int_0^1 |\widehat{f}(\theta)|^4 e(a\theta) \mathrm{d} \theta \leq \|f\|_4^4.
\end{equation*}
\begin{equation*}
\sum_{\substack{a_1,a_2,a_3,a_4 \in \mathbb{Z} \\ a_3+a_4-a_1-a_2=a}} f(a_1) f(a_2) f(a_3) f(a_4) = \int_0^1 |\widehat{f}(\theta)|^4 e(a\theta) \mathrm{d} \theta \leq \|f\|_4^4.
\end{equation*}Hence,
 \begin{equation*} \|\widehat{g_M}\|_4^4 \leq \left(1 + O(k^{-1/2})\right) \|f\|_4^4 \sum_{a \in \mathbb{Z}} I(0,0,0,a) = \left(1 + O(k^{-1/2})\right) \|f\|_4^4. \end{equation*}
\begin{equation*} \|\widehat{g_M}\|_4^4 \leq \left(1 + O(k^{-1/2})\right) \|f\|_4^4 \sum_{a \in \mathbb{Z}} I(0,0,0,a) = \left(1 + O(k^{-1/2})\right) \|f\|_4^4. \end{equation*}This proves the first bound in the lemma. For the second bound concerning the Lq-norms, note that
 \begin{equation*} \|f\|_q^q - \|g_M\|_q^q = \sum_{a \in \mathbb{Z}} f(a)^q - \int_{-\infty}^{\infty} g_M(x)^q \mathrm{d} x = \sum_{a \in \mathbb{Z}} \left(f(a)^q - \int_a^{a+1} g_M(x)^q \mathrm{d} x\right). \end{equation*}
\begin{equation*} \|f\|_q^q - \|g_M\|_q^q = \sum_{a \in \mathbb{Z}} f(a)^q - \int_{-\infty}^{\infty} g_M(x)^q \mathrm{d} x = \sum_{a \in \mathbb{Z}} \left(f(a)^q - \int_a^{a+1} g_M(x)^q \mathrm{d} x\right). \end{equation*}By lemma 3.3, we have
 \begin{equation*} \int_a^{a+1} g_M(x)^q \mathrm{d} x = (1+O(k^{-1/2})) f(a)^q \end{equation*}
\begin{equation*} \int_a^{a+1} g_M(x)^q \mathrm{d} x = (1+O(k^{-1/2})) f(a)^q \end{equation*} for every ![]() $a \in \mathbb{Z}$. It follows that
$a \in \mathbb{Z}$. It follows that
 \begin{equation*} \|f\|_q^q - \|g_M\|_q^q = O\left(k^{-1/2} \sum_{a \in \mathbb{Z}} f(a)^q\right) = O\left(k^{-1/2} \|f\|_q^q\right). \end{equation*}
\begin{equation*} \|f\|_q^q - \|g_M\|_q^q = O\left(k^{-1/2} \sum_{a \in \mathbb{Z}} f(a)^q\right) = O\left(k^{-1/2} \|f\|_q^q\right). \end{equation*}This proves the second bound in the lemma.
We may now complete the proof of proposition 2.2 by combining the lemmas above. Indeed, by lemmas 3.2 and 3.4, we have
 \begin{equation*} \|f\|_q \leq (1 + O(k^{-1/2})) \|g_M\|_q \leq (1 + O(k^{-1/2})) \|g\|_q \end{equation*}
\begin{equation*} \|f\|_q \leq (1 + O(k^{-1/2})) \|g_M\|_q \leq (1 + O(k^{-1/2})) \|g\|_q \end{equation*}and
 \begin{equation*} \|\widehat{f}\|_4 \geq (1 - O(k^{-1/2})) \|\widehat{g_M}\|_4 \geq (1 - O(k^{-1/2})) \left(\|\widehat{g}\|_4 - \exp(-k^{\varepsilon/20})\right). \end{equation*}
\begin{equation*} \|\widehat{f}\|_4 \geq (1 - O(k^{-1/2})) \|\widehat{g_M}\|_4 \geq (1 - O(k^{-1/2})) \left(\|\widehat{g}\|_4 - \exp(-k^{\varepsilon/20})\right). \end{equation*} Since ![]() $\|\widehat{g}\|_4 \asymp A^{3/8}$, we have
$\|\widehat{g}\|_4 \asymp A^{3/8}$, we have
 \begin{equation*} \|\widehat{f}\|_4 \geq (1 - O(k^{-1/2})) \|\widehat{g}\|_4. \end{equation*}
\begin{equation*} \|\widehat{f}\|_4 \geq (1 - O(k^{-1/2})) \|\widehat{g}\|_4. \end{equation*}It follows from lemma 3.1 that
 \begin{equation*} \frac{\|\widehat{f}\|_4}{\|f\|_q} \geq (1-O(k^{-1/2})) \frac{\|\widehat{g}\|_4}{\|g\|_q} \geq (1 - O(k^{-1/2})) (1 + c\varepsilon) \gt 1, \end{equation*}
\begin{equation*} \frac{\|\widehat{f}\|_4}{\|f\|_q} \geq (1-O(k^{-1/2})) \frac{\|\widehat{g}\|_4}{\|g\|_q} \geq (1 - O(k^{-1/2})) (1 + c\varepsilon) \gt 1, \end{equation*}once k is large enough in terms of ɛ.
4. Upper bound for tn
In this section, we prove proposition 2.3. As explained in § 2, a key ingredient is an approximate inverse theorem for Young’s convolution inequality, proposition 4.5, which is a special case of results in [Reference Charalambides and Christ4, Reference Eisner and Tao7]. For completeness, we give a self-contained proof of it. In preparation for the proof, we start with establishing an approximate inverse theorem for Hölder’s inequality, lemma 4.3, which is a special case of [Reference Eisner and Tao7, lemma 5.1].
4.1. Near equality in Hölder’s inequality
In this section, all implied constants are allowed to depend on the exponents p,q, and r.
Lemma 4.1. Let ![]() $p,q \in (1,+\infty)$ be exponents with
$p,q \in (1,+\infty)$ be exponents with ![]() $1/p + 1/q = 1$. Let
$1/p + 1/q = 1$. Let ![]() $a, b$ be non-negative reals. Suppose that
$a, b$ be non-negative reals. Suppose that
 \begin{equation*} \frac{a^p}{p} + \frac{b^q}{q} \leq (1 + \delta)ab \end{equation*}
\begin{equation*} \frac{a^p}{p} + \frac{b^q}{q} \leq (1 + \delta)ab \end{equation*} for some sufficiently small constant δ > 0. Then, ![]() $a^p = (1 + O(\delta^{1/2}))b^q$.
$a^p = (1 + O(\delta^{1/2}))b^q$.
Proof. If ab = 0, then the conclusion holds trivially. Henceforth, assume that ![]() $a,b \gt 0$. By Taylor’s theorem applied to the function
$a,b \gt 0$. By Taylor’s theorem applied to the function ![]() $\psi(x) = \log x$ at the point
$\psi(x) = \log x$ at the point ![]() $x_0 = a^p/p + b^q/q$, we have
$x_0 = a^p/p + b^q/q$, we have
 \begin{equation*} \psi(a^p) = \psi(x_0) + (a^p - x_0) \psi'(x_0) + \frac{1}{2} (a^p-x_0)^2 \psi''(\xi_1) \end{equation*}
\begin{equation*} \psi(a^p) = \psi(x_0) + (a^p - x_0) \psi'(x_0) + \frac{1}{2} (a^p-x_0)^2 \psi''(\xi_1) \end{equation*}and
 \begin{equation*} \psi(b^q) = \psi(x_0) + (b^q - x_0) \psi'(x_0) + \frac{1}{2} (b^q-x_0)^2 \psi''(\xi_2) \end{equation*}
\begin{equation*} \psi(b^q) = \psi(x_0) + (b^q - x_0) \psi'(x_0) + \frac{1}{2} (b^q-x_0)^2 \psi''(\xi_2) \end{equation*} for some ![]() $\xi_1,\xi_2$ lying between ap and bq. Since
$\xi_1,\xi_2$ lying between ap and bq. Since
 \begin{equation*} a^p - x_0 = \frac{a^p - b^q}{q}, \ \ b^q-x_0 = \frac{b^q-a^p}{p}, \end{equation*}
\begin{equation*} a^p - x_0 = \frac{a^p - b^q}{q}, \ \ b^q-x_0 = \frac{b^q-a^p}{p}, \end{equation*}it follows that
 \begin{equation*} \frac{1}{p}\psi(a^p) + \frac{1}{q}\psi(b^q) = \psi(x_0) + \frac{(a^p-b^q)^2}{2pq^2} \psi''(\xi_1) + \frac{(a^p-b^q)^2}{2p^2q}\psi''(\xi_2). \end{equation*}
\begin{equation*} \frac{1}{p}\psi(a^p) + \frac{1}{q}\psi(b^q) = \psi(x_0) + \frac{(a^p-b^q)^2}{2pq^2} \psi''(\xi_1) + \frac{(a^p-b^q)^2}{2p^2q}\psi''(\xi_2). \end{equation*} Since ![]() $\psi''(x) = -1/x^2$, we have
$\psi''(x) = -1/x^2$, we have
 \begin{equation*} \psi''(\xi_i) \leq -\min\left(\frac{1}{a^{2p}}, \frac{1}{b^{2q}}\right). \end{equation*}
\begin{equation*} \psi''(\xi_i) \leq -\min\left(\frac{1}{a^{2p}}, \frac{1}{b^{2q}}\right). \end{equation*}From hypothesis, we have
 \begin{equation*} \frac{1}{p}\psi(a^p) + \frac{1}{q}\psi(b^q) - \psi(x_0) = \log a + \log b - \log\left(\frac{a^p}{p} + \frac{b^q}{q}\right) \geq -\log(1+\delta) \geq - \delta. \end{equation*}
\begin{equation*} \frac{1}{p}\psi(a^p) + \frac{1}{q}\psi(b^q) - \psi(x_0) = \log a + \log b - \log\left(\frac{a^p}{p} + \frac{b^q}{q}\right) \geq -\log(1+\delta) \geq - \delta. \end{equation*}Hence, it follows that
 \begin{equation*} -\delta \leq -(a^p-b^q)^2\left(\frac{1}{2pq^2} + \frac{1}{2p^2q}\right) \min\left(\frac{1}{a^{2p}}, \frac{1}{b^{2q}}\right) = -\frac{(a^p-b^q)^2}{2pq} \min\left(\frac{1}{a^{2p}}, \frac{1}{b^{2q}}\right), \end{equation*}
\begin{equation*} -\delta \leq -(a^p-b^q)^2\left(\frac{1}{2pq^2} + \frac{1}{2p^2q}\right) \min\left(\frac{1}{a^{2p}}, \frac{1}{b^{2q}}\right) = -\frac{(a^p-b^q)^2}{2pq} \min\left(\frac{1}{a^{2p}}, \frac{1}{b^{2q}}\right), \end{equation*}and thus,
The desired conclusion follows immediately.
Lemma 4.2. Let ![]() $p,q,r \in (1,+\infty)$ be exponents with
$p,q,r \in (1,+\infty)$ be exponents with ![]() $1/p + 1/q + 1/r = 1$. Let a, b, and c be non-negative reals. Suppose that
$1/p + 1/q + 1/r = 1$. Let a, b, and c be non-negative reals. Suppose that
 \begin{equation*} \frac{a^p}{p} + \frac{b^q}{q} + \frac{c^r}{r} \leq (1 + \delta)abc \end{equation*}
\begin{equation*} \frac{a^p}{p} + \frac{b^q}{q} + \frac{c^r}{r} \leq (1 + \delta)abc \end{equation*} for some sufficiently small constant δ > 0. Then, ![]() $a^p = (1 + O(\delta^{1/2}))b^q = (1 + O(\delta^{1/2})c^r$.
$a^p = (1 + O(\delta^{1/2}))b^q = (1 + O(\delta^{1/2})c^r$.
Proof. We may assume that abc > 0, since otherwise the conclusion holds trivially. Choose exponent ![]() $p' \in (1,+\infty)$ such that
$p' \in (1,+\infty)$ such that ![]() $1/p + 1/p' = 1$. Let
$1/p + 1/p' = 1$. Let
 \begin{equation*} d = \left(\frac{p'}{q} b^q + \frac{p'}{r} c^r\right)^{1/p'}. \end{equation*}
\begin{equation*} d = \left(\frac{p'}{q} b^q + \frac{p'}{r} c^r\right)^{1/p'}. \end{equation*}Then,
 \begin{equation*} \frac{a^p}{p} + \frac{b^q}{q} + \frac{c^r}{r} = \frac{a^p}{p} + \frac{d^{p'}}{p'} \geq ad. \end{equation*}
\begin{equation*} \frac{a^p}{p} + \frac{b^q}{q} + \frac{c^r}{r} = \frac{a^p}{p} + \frac{d^{p'}}{p'} \geq ad. \end{equation*} From hypothesis, it follows that ![]() $d \leq (1+\delta)bc$, which can be rewritten as
$d \leq (1+\delta)bc$, which can be rewritten as
 \begin{equation*} \frac{x^{q'}}{q'} + \frac{y^{r'}}{r'} \leq (1+\delta)^{p'} xy, \end{equation*}
\begin{equation*} \frac{x^{q'}}{q'} + \frac{y^{r'}}{r'} \leq (1+\delta)^{p'} xy, \end{equation*}where
 \begin{equation*} q' = \frac{q}{p'}, \ \ r' = \frac{r}{p'}, \ \ x = b^{p'}, \text{and} \ \ y = c^{q'}. \end{equation*}
\begin{equation*} q' = \frac{q}{p'}, \ \ r' = \frac{r}{p'}, \ \ x = b^{p'}, \text{and} \ \ y = c^{q'}. \end{equation*} Note that ![]() $1/q' + 1/r' = 1$. Hence, by lemma 4.1, it follows that
$1/q' + 1/r' = 1$. Hence, by lemma 4.1, it follows that
 \begin{equation*} x^{q'} = (1 + O(\delta^{1/2})) y^{r'}, \end{equation*}
\begin{equation*} x^{q'} = (1 + O(\delta^{1/2})) y^{r'}, \end{equation*}which implies that
Similarly, one can also prove that ![]() $a^p = (1 + O(\delta^{1/2})) c^r$.
$a^p = (1 + O(\delta^{1/2})) c^r$.
Lemma 4.3. Let ![]() $p,q,r \in (1,+\infty)$ be exponents with
$p,q,r \in (1,+\infty)$ be exponents with ![]() $1/p + 1/q + 1/r = 1$. Let
$1/p + 1/q + 1/r = 1$. Let ![]() $a_1,\cdots,a_n$,
$a_1,\cdots,a_n$, ![]() $b_1,\cdots,b_n$,
$b_1,\cdots,b_n$, ![]() $c_1,\cdots,c_n$ be non-negative reals such that
$c_1,\cdots,c_n$ be non-negative reals such that
 \begin{equation*} \sum_{i=1}^n a_i^p = \sum_{i=1}^n b_i^q = \sum_{i=1}^n c_i^r = 1. \end{equation*}
\begin{equation*} \sum_{i=1}^n a_i^p = \sum_{i=1}^n b_i^q = \sum_{i=1}^n c_i^r = 1. \end{equation*}Suppose that
 \begin{equation*} \sum_{i=1}^n a_ib_ic_i \geq 1 - \delta \end{equation*}
\begin{equation*} \sum_{i=1}^n a_ib_ic_i \geq 1 - \delta \end{equation*}for some sufficiently small constant δ > 0. Then, we have
 \begin{equation*} a_i^p = (1 + O(\delta^{1/4})) b_i^q = (1 + O(\delta^{1/4})) c_i^r \end{equation*}
\begin{equation*} a_i^p = (1 + O(\delta^{1/4})) b_i^q = (1 + O(\delta^{1/4})) c_i^r \end{equation*}for each i outside an exceptional set E satisfying
 \begin{equation*} \sum_{i \in E} (a_i^p + b_i^q + c_i^r) \ll \delta^{1/2}. \end{equation*}
\begin{equation*} \sum_{i \in E} (a_i^p + b_i^q + c_i^r) \ll \delta^{1/2}. \end{equation*}Proof. For each i, we have
 \begin{equation*} a_ib_ic_i \leq \frac{a_i^p}{p} + \frac{b_i^q}{q} + \frac{c_i^r}{r}. \end{equation*}
\begin{equation*} a_ib_ic_i \leq \frac{a_i^p}{p} + \frac{b_i^q}{q} + \frac{c_i^r}{r}. \end{equation*} Let ![]() $E \subset \{1,2,\cdots,n\}$ be the exceptional set of indices i such that
$E \subset \{1,2,\cdots,n\}$ be the exceptional set of indices i such that
 \begin{equation*} \frac{a_i^p}{p} + \frac{b_i^q}{q} + \frac{c_i^r}{r} \geq (1+\delta^{1/2}) a_ib_ic_i. \end{equation*}
\begin{equation*} \frac{a_i^p}{p} + \frac{b_i^q}{q} + \frac{c_i^r}{r} \geq (1+\delta^{1/2}) a_ib_ic_i. \end{equation*}Then,
 \begin{equation*} \delta \geq \sum_{i=1}^n \left(\frac{a_i^p}{p} + \frac{b_i^q}{q} + \frac{c_i^r}{r} - a_ib_ic_i\right) \gg \delta^{1/2} \sum_{i \in E} \left(\frac{a_i^p}{p} + \frac{b_i^q}{q} + \frac{c_i^r}{r}\right), \end{equation*}
\begin{equation*} \delta \geq \sum_{i=1}^n \left(\frac{a_i^p}{p} + \frac{b_i^q}{q} + \frac{c_i^r}{r} - a_ib_ic_i\right) \gg \delta^{1/2} \sum_{i \in E} \left(\frac{a_i^p}{p} + \frac{b_i^q}{q} + \frac{c_i^r}{r}\right), \end{equation*} and hence,  $\sum_{i \in E} (a_i^p + b_i^q + c_i^r) \ll \delta^{1/2}$. For
$\sum_{i \in E} (a_i^p + b_i^q + c_i^r) \ll \delta^{1/2}$. For ![]() $i \notin E$, lemma 4.2 implies that
$i \notin E$, lemma 4.2 implies that
 \begin{equation*} a_i^p = (1 + O(\delta^{1/4})) b_i^q = (1 + O(\delta^{1/4})) c_i^r. \end{equation*}
\begin{equation*} a_i^p = (1 + O(\delta^{1/4})) b_i^q = (1 + O(\delta^{1/4})) c_i^r. \end{equation*}This concludes the proof.
4.2. Near equality in Young’s inequality
In this section, all implied constants are allowed to depend on the exponents p, q, and r. Before proving the approximate inverse of Young’s inequality, we need the following standard result in additive combinatorics.
Lemma 4.4. Let G be an abelian group and let ![]() $X, Y \subset G$ be finite subsets with
$X, Y \subset G$ be finite subsets with ![]() $|X| = |Y| = N$. Let
$|X| = |Y| = N$. Let ![]() $\varepsilon \in (0, 1/20)$ and let δ > 0 be sufficiently small in terms of ɛ. Let
$\varepsilon \in (0, 1/20)$ and let δ > 0 be sufficiently small in terms of ɛ. Let ![]() $M \subset X \times Y$ be a subset with
$M \subset X \times Y$ be a subset with ![]() $|M| \geq (1-\delta) N^2$. Suppose that the restricted sumset
$|M| \geq (1-\delta) N^2$. Suppose that the restricted sumset
has size at most ![]() $(1+\varepsilon)N$. Then, there exists a coset x + H of a subgroup
$(1+\varepsilon)N$. Then, there exists a coset x + H of a subgroup ![]() $H \subset G$ such that
$H \subset G$ such that ![]() $|X \setminus (x+H)| \leq \varepsilon N$ and
$|X \setminus (x+H)| \leq \varepsilon N$ and ![]() $|(x+H) \setminus X| \leq 3\varepsilon N$.
$|(x+H) \setminus X| \leq 3\varepsilon N$.
Proof. By an almost-all version of the Balog–Szemeredi–Gowers theorem as in [Reference Shao13, theorem 1.1] (see also [Reference Shao and Xu14, theorem 1.1] for a version with ![]() $G = \mathbb{Z}$ and [Reference Campos, Coulson, Serra and Wötzel3, theorem 3.3] for an asymmetric version), one can find subsets
$G = \mathbb{Z}$ and [Reference Campos, Coulson, Serra and Wötzel3, theorem 3.3] for an asymmetric version), one can find subsets ![]() $X' \subset X$ and
$X' \subset X$ and ![]() $Y' \subset Y$ such that
$Y' \subset Y$ such that
By Kneser’s theorem [Reference Kneser10] (see [Reference Tao and Vu15, theorem 5.5]), we have
where ![]() $H \subset G$ is the subgroup defined by
$H \subset G$ is the subgroup defined by
It follows that ![]() $|H| \geq (1-4\varepsilon)N$ and hence
$|H| \geq (1-4\varepsilon)N$ and hence ![]() $|X'+Y'| \lt 2|H|$. Since
$|X'+Y'| \lt 2|H|$. Since ![]() $X'+Y'$ is the union of cosets of H, it must be a single coset of H, and thus X ʹ is contained in a single coset x + H of H. Hence,
$X'+Y'$ is the union of cosets of H, it must be a single coset of H, and thus X ʹ is contained in a single coset x + H of H. Hence,
and
Proposition 4.5. Let ![]() $p,q,r \in (1,+\infty)$ be exponents with
$p,q,r \in (1,+\infty)$ be exponents with ![]() $1/p + 1/q = 1 + 1/r$. Let
$1/p + 1/q = 1 + 1/r$. Let ![]() $f,g: \mathbb{Z}\rightarrow\mathbb{C}$ be finitely supported functions such that
$f,g: \mathbb{Z}\rightarrow\mathbb{C}$ be finitely supported functions such that ![]() $\|f\|_p = \|g\|_q = 1$. Suppose that
$\|f\|_p = \|g\|_q = 1$. Suppose that
for some sufficiently small constant δ > 0. Then, there exists a singleton set ![]() $\{x_0\}$ for some
$\{x_0\}$ for some ![]() $x_0 \in \mathbb{Z}$ such that
$x_0 \in \mathbb{Z}$ such that
 \begin{equation*} \|f - f(x_0)1_{\{x_0\}}\|_p^p \ll \delta^{1/8}. \end{equation*}
\begin{equation*} \|f - f(x_0)1_{\{x_0\}}\|_p^p \ll \delta^{1/8}. \end{equation*}Proof. By replacing ![]() $f,g$ by
$f,g$ by ![]() $|f|, |g|$, we may assume that
$|f|, |g|$, we may assume that ![]() $f,g$ take non-negative real values. For every
$f,g$ take non-negative real values. For every ![]() $x \in \mathbb{Z}$, we have
$x \in \mathbb{Z}$, we have
 \begin{equation*} (f*g)(x) = \sum_{y\in\mathbb{Z}} f(x-y) g(y) = \sum_{y \in \mathbb{Z}} f(x-y)^{p/r} g(y)^{q/r} \cdot f(x-y)^{(r-p)/r} \cdot g(y)^{(r-q)/r}. \end{equation*}
\begin{equation*} (f*g)(x) = \sum_{y\in\mathbb{Z}} f(x-y) g(y) = \sum_{y \in \mathbb{Z}} f(x-y)^{p/r} g(y)^{q/r} \cdot f(x-y)^{(r-p)/r} \cdot g(y)^{(r-q)/r}. \end{equation*}By Hölder’s inequality, we have
 \begin{equation}
(f*g)(x) \leq \left(\sum_{y \in \mathbb{Z}} f(x-y)^p g(y)^q \right)^{\frac{1}{r}} \left(\sum_{y \in \mathbb{Z}} f(x-y)^p\right)^{\frac{r-p}{pr}} \left(\sum_{y \in \mathbb{Z}} g(y)^q\right)^{\frac{r-q}{qr}}.
\end{equation}
\begin{equation}
(f*g)(x) \leq \left(\sum_{y \in \mathbb{Z}} f(x-y)^p g(y)^q \right)^{\frac{1}{r}} \left(\sum_{y \in \mathbb{Z}} f(x-y)^p\right)^{\frac{r-p}{pr}} \left(\sum_{y \in \mathbb{Z}} g(y)^q\right)^{\frac{r-q}{qr}}.
\end{equation} Since ![]() $\|f\|_p = \|g\|_q = 1$, it follows that
$\|f\|_p = \|g\|_q = 1$, it follows that
 \begin{equation*} (f*g)(x)^r \leq \sum_{y \in \mathbb{Z}} f(x-y)^p g(y)^q. \end{equation*}
\begin{equation*} (f*g)(x)^r \leq \sum_{y \in \mathbb{Z}} f(x-y)^p g(y)^q. \end{equation*} Let ![]() $E_1 \subset \mathbb{Z}$ be the exceptional set of
$E_1 \subset \mathbb{Z}$ be the exceptional set of ![]() $x \in \mathbb{Z}$ such that
$x \in \mathbb{Z}$ such that
 \begin{equation*} (f*g)(x)^r \leq (1 - \delta^{1/2}) \sum_{y \in \mathbb{Z}} f(x-y)^p g(y)^q. \end{equation*}
\begin{equation*} (f*g)(x)^r \leq (1 - \delta^{1/2}) \sum_{y \in \mathbb{Z}} f(x-y)^p g(y)^q. \end{equation*}From hypothesis, we have
 \begin{align*} 1 - (1-\delta)^r & \geq \sum_{x \in \mathbb{Z}} \left(\sum_{y \in \mathbb{Z}} f(x-y)^p g(y)^q - (f*g)(x)^r\right) \\
& \geq \delta^{1/2} \sum_{x \in E_1} \sum_{y \in \mathbb{Z}} f(x-y)^p g(y)^q, \end{align*}
\begin{align*} 1 - (1-\delta)^r & \geq \sum_{x \in \mathbb{Z}} \left(\sum_{y \in \mathbb{Z}} f(x-y)^p g(y)^q - (f*g)(x)^r\right) \\
& \geq \delta^{1/2} \sum_{x \in E_1} \sum_{y \in \mathbb{Z}} f(x-y)^p g(y)^q, \end{align*}and hence,
 \begin{equation}
\sum_{(x,y) \in E_1\times \mathbb{Z}} f(x-y)^p g(y)^q \ll \delta^{1/2}.
\end{equation}
\begin{equation}
\sum_{(x,y) \in E_1\times \mathbb{Z}} f(x-y)^p g(y)^q \ll \delta^{1/2}.
\end{equation} For each ![]() $x \notin E_1$, we have almost equality in (4.1), and hence, by lemma 4.3 applied to the three sequences
$x \notin E_1$, we have almost equality in (4.1), and hence, by lemma 4.3 applied to the three sequences
 \begin{equation*} a_x(y) = \frac{f(x-y)^{p/r} g(y)^{q/r}}{h(x)^{1/r}}, \ \ b_x(y) = f(x-y)^{(r-p)/r}, \ \ c_x(y) = g(y)^{(r-q)/r}, \end{equation*}
\begin{equation*} a_x(y) = \frac{f(x-y)^{p/r} g(y)^{q/r}}{h(x)^{1/r}}, \ \ b_x(y) = f(x-y)^{(r-p)/r}, \ \ c_x(y) = g(y)^{(r-q)/r}, \end{equation*}where
 \begin{equation*} h(x) = \sum_{z \in \mathbb{Z}} f(x-z)^p g(z)^q, \end{equation*}
\begin{equation*} h(x) = \sum_{z \in \mathbb{Z}} f(x-z)^p g(z)^q, \end{equation*}we conclude that
 \begin{equation}
\frac{f(x-y)^pg(y)^q}{h(x)} = (1 + O(\delta^{1/8})) f(x-y)^p = (1 + O(\delta^{1/8})) g(y)^q
\end{equation}
\begin{equation}
\frac{f(x-y)^pg(y)^q}{h(x)} = (1 + O(\delta^{1/8})) f(x-y)^p = (1 + O(\delta^{1/8})) g(y)^q
\end{equation} for each y outside an exceptional set ![]() $E_2(x)$ satisfying
$E_2(x)$ satisfying
 \begin{equation}
\sum_{y \in E_2(x)} f(x-y)^p g(y)^q \ll \delta^{1/4}h(x).
\end{equation}
\begin{equation}
\sum_{y \in E_2(x)} f(x-y)^p g(y)^q \ll \delta^{1/4}h(x).
\end{equation}Define
Then, from (4.2) and (4.4), it follows that
 \begin{equation*} \sum_{(x,y) \in E} f(x-y)^p g(y)^q \ll \delta^{1/2} + \delta^{1/4} \sum_{x \in \mathbb{Z}}h(x) \ll \delta^{1/4}, \end{equation*}
\begin{equation*} \sum_{(x,y) \in E} f(x-y)^p g(y)^q \ll \delta^{1/2} + \delta^{1/4} \sum_{x \in \mathbb{Z}}h(x) \ll \delta^{1/4}, \end{equation*} and (4.3) holds for every ![]() $(x,y) \notin E$.
$(x,y) \notin E$.
Now make a change of variables and consider
Then,
 \begin{equation}
\sum_{(x,y) \in E'} f(x)^p g(y)^q = \sum_{(x,y) \in E} f(x-y)^pg(y)^q \ll \delta^{1/4},
\end{equation}
\begin{equation}
\sum_{(x,y) \in E'} f(x)^p g(y)^q = \sum_{(x,y) \in E} f(x-y)^pg(y)^q \ll \delta^{1/4},
\end{equation}and we have
 \begin{equation}
\frac{f(x)^p g(y)^q}{h(x+y)} = (1 + O(\delta^{1/8}))f(x)^p = (1 + O(\delta^{1/8})) g(y)^q
\end{equation}
\begin{equation}
\frac{f(x)^p g(y)^q}{h(x+y)} = (1 + O(\delta^{1/8}))f(x)^p = (1 + O(\delta^{1/8})) g(y)^q
\end{equation} for every ![]() $(x,y) \notin E'$. Let
$(x,y) \notin E'$. Let ![]() $X \subset \mathbb{Z}$ be the set of
$X \subset \mathbb{Z}$ be the set of ![]() $x \in \mathbb{Z}$ such that
$x \in \mathbb{Z}$ such that
 \begin{equation*} \sum_{y: (x,y) \in E'} g(y)^q \leq \delta^{1/8}. \end{equation*}
\begin{equation*} \sum_{y: (x,y) \in E'} g(y)^q \leq \delta^{1/8}. \end{equation*}Then, from (4.5), it follows that
 \begin{equation*} \delta^{1/4} \gg \sum_{x \notin X} f(x)^p \sum_{y: (x,y) \in E'} g(y)^q \geq \delta^{1/8} \sum_{x \notin X} f(x)^p, \end{equation*}
\begin{equation*} \delta^{1/4} \gg \sum_{x \notin X} f(x)^p \sum_{y: (x,y) \in E'} g(y)^q \geq \delta^{1/8} \sum_{x \notin X} f(x)^p, \end{equation*}and hence,
 \begin{equation}
\sum_{x\notin X} f(x)^p \ll \delta^{1/8}.
\end{equation}
\begin{equation}
\sum_{x\notin X} f(x)^p \ll \delta^{1/8}.
\end{equation} For every ![]() $x_1, x_2 \in X$, since
$x_1, x_2 \in X$, since
 \begin{equation*} \sum_{y: (x_1,y) \in E'} g(y)^q + \sum_{y: (x_2,y) \in E'} g(y)^q \ll \delta^{1/8}, \end{equation*}
\begin{equation*} \sum_{y: (x_1,y) \in E'} g(y)^q + \sum_{y: (x_2,y) \in E'} g(y)^q \ll \delta^{1/8}, \end{equation*} there exists ![]() $y \in \mathbb{Z}$ such that
$y \in \mathbb{Z}$ such that ![]() $(x_1,y) \notin E'$ and
$(x_1,y) \notin E'$ and ![]() $(x_2,y)\notin E'$. By (4.6), we have
$(x_2,y)\notin E'$. By (4.6), we have
We conclude that there exists a constant ![]() $a \in \mathbb{R}$ such that
$a \in \mathbb{R}$ such that
for every ![]() $x \in X$. Moreover, since
$x \in X$. Moreover, since
 \begin{equation*} 1 = \sum_{x \in \mathbb{Z}} f(x)^p = \sum_{x \in X} f(x)^p + O(\delta^{1/8}) = (1 + O(\delta^{1/8})) a^p |X| + O(\delta^{1/8}), \end{equation*}
\begin{equation*} 1 = \sum_{x \in \mathbb{Z}} f(x)^p = \sum_{x \in X} f(x)^p + O(\delta^{1/8}) = (1 + O(\delta^{1/8})) a^p |X| + O(\delta^{1/8}), \end{equation*}we have
By symmetry, we may also conclude the existence of a constant ![]() $b \in \mathbb{R}$ such that
$b \in \mathbb{R}$ such that
for every ![]() $y \in Y$, where
$y \in Y$, where ![]() $Y \subset \mathbb{Z}$ is a subset satisfying
$Y \subset \mathbb{Z}$ is a subset satisfying
We now return to using the first part of (4.6) for ![]() $(x,y) \in M := (X \times Y)\setminus E'$. First note from (4.5) that
$(x,y) \in M := (X \times Y)\setminus E'$. First note from (4.5) that
 \begin{equation*} \delta^{1/4} \gg \sum_{(x,y) \in (X\times Y) \cap E'} f(x)^p g(y)^q \gg a^p b^q \cdot |(X\times Y) \cap E'| \gg |X|^{-1}|Y|^{-1} \cdot |(X\times Y) \cap E'|, \end{equation*}
\begin{equation*} \delta^{1/4} \gg \sum_{(x,y) \in (X\times Y) \cap E'} f(x)^p g(y)^q \gg a^p b^q \cdot |(X\times Y) \cap E'| \gg |X|^{-1}|Y|^{-1} \cdot |(X\times Y) \cap E'|, \end{equation*}and hence,
For ![]() $(x,y) \in M$, (4.6) implies that
$(x,y) \in M$, (4.6) implies that
 \begin{equation*} \frac{a^pb^q}{h(x+y)} = (1 + O(\delta^{1/8}) a^p = (1 + O(\delta^{1/8})) b^q. \end{equation*}
\begin{equation*} \frac{a^pb^q}{h(x+y)} = (1 + O(\delta^{1/8}) a^p = (1 + O(\delta^{1/8})) b^q. \end{equation*} In particular, since M is non-empty, we have ![]() $a^p = (1 + O(\delta^{1/8})) b^q$, and hence,
$a^p = (1 + O(\delta^{1/8})) b^q$, and hence, ![]() $|X| = (1 + O(\delta^{1/8})) |Y|$. Moreover, for
$|X| = (1 + O(\delta^{1/8})) |Y|$. Moreover, for ![]() $s \in X+_MY$, we have
$s \in X+_MY$, we have
Since ![]() $\sum_{s \in \mathbb{Z}}h(s) = 1$, we have
$\sum_{s \in \mathbb{Z}}h(s) = 1$, we have
 \begin{equation*} 1 \geq \sum_{s \in X+_MY} h(s) = (1 - O(\delta^{1/8}))a^p \cdot |X+_MY|, \end{equation*}
\begin{equation*} 1 \geq \sum_{s \in X+_MY} h(s) = (1 - O(\delta^{1/8}))a^p \cdot |X+_MY|, \end{equation*}and hence,
We now apply lemma 4.4 with ![]() $\varepsilon = 1/100$ (say), after possibly shrinking one of
$\varepsilon = 1/100$ (say), after possibly shrinking one of ![]() $X, Y$ slightly so that
$X, Y$ slightly so that ![]() $|X| = |Y|$, to conclude that there exists a coset
$|X| = |Y|$, to conclude that there exists a coset ![]() $x_0 + H$ of a subgroup
$x_0 + H$ of a subgroup ![]() $H \subset \mathbb{Z}$ such that
$H \subset \mathbb{Z}$ such that
 \begin{equation*} |X \setminus (x_0+H)| \leq \frac{1}{10}|X|, \ \ |(x_0+H) \setminus X| \leq \frac{1}{10}|X|. \end{equation*}
\begin{equation*} |X \setminus (x_0+H)| \leq \frac{1}{10}|X|, \ \ |(x_0+H) \setminus X| \leq \frac{1}{10}|X|. \end{equation*} The only finite subgroup of ![]() $\mathbb{Z}$ is
$\mathbb{Z}$ is ![]() $H = \{0\}$, and hence, it must be that
$H = \{0\}$, and hence, it must be that ![]() $X = \{x_0\}$. The desired conclusions follow immediately from (4.7).
$X = \{x_0\}$. The desired conclusions follow immediately from (4.7).
4.3. Proof of proposition 2.3
Let ![]() $f: \mathbb{Z} \rightarrow \mathbb{R}$ be a function that is supported on a set of size
$f: \mathbb{Z} \rightarrow \mathbb{R}$ be a function that is supported on a set of size ![]() $n \geq 2$. By replacing f by
$n \geq 2$. By replacing f by ![]() $|f|$, we may assume that f takes non-negative real values. Let δ > 0 be a sufficiently small absolute constant and let
$|f|$, we may assume that f takes non-negative real values. Let δ > 0 be a sufficiently small absolute constant and let
 \begin{equation*} q = \frac{4}{3 - \log_n(1+\delta)}. \end{equation*}
\begin{equation*} q = \frac{4}{3 - \log_n(1+\delta)}. \end{equation*}First, consider the case when
 \begin{equation*} \|\widehat{f}\|_4 \leq (1 - \delta) \|f\|_{4/3}. \end{equation*}
\begin{equation*} \|\widehat{f}\|_4 \leq (1 - \delta) \|f\|_{4/3}. \end{equation*}By Hölder’s inequality (see (2.2)), we have
 \begin{equation*} \|f\|_{4/3} \leq n^{3/4-1/q} \|f\|_q = (1+\delta)^{1/4} \|f\|_q. \end{equation*}
\begin{equation*} \|f\|_{4/3} \leq n^{3/4-1/q} \|f\|_q = (1+\delta)^{1/4} \|f\|_q. \end{equation*}It follows that
 \begin{equation*} \|\widehat{f}\|_4 \leq (1-\delta) (1+\delta)^{1/4} \|f\|_q \leq \|f\|_q. \end{equation*}
\begin{equation*} \|\widehat{f}\|_4 \leq (1-\delta) (1+\delta)^{1/4} \|f\|_q \leq \|f\|_q. \end{equation*}Now suppose that
 \begin{equation*} \|\widehat{f}\|_4 \geq (1 - \delta) \|f\|_{4/3}. \end{equation*}
\begin{equation*} \|\widehat{f}\|_4 \geq (1 - \delta) \|f\|_{4/3}. \end{equation*} By normalization, we may assume that ![]() $\|f\|_{4/3} = 1$, and thus,
$\|f\|_{4/3} = 1$, and thus,  $\|f*f\|_2 = \|\widehat{f}\|_4^2 \geq 1-2\delta$. By proposition 4.5, there exists
$\|f*f\|_2 = \|\widehat{f}\|_4^2 \geq 1-2\delta$. By proposition 4.5, there exists ![]() $x_0 \in \mathbb{Z}$ such that
$x_0 \in \mathbb{Z}$ such that
 \begin{equation}
\|f - f(x_0)1_{\{x_0\}}\|_{4/3} \ll \delta^{1/20}.
\end{equation}
\begin{equation}
\|f - f(x_0)1_{\{x_0\}}\|_{4/3} \ll \delta^{1/20}.
\end{equation} By translation, we may assume that ![]() $x_0=0$, and we may write f in the form
$x_0=0$, and we may write f in the form ![]() $f = f(0)\delta_0 + g$, where δ 0 is the Kronecker delta function and
$f = f(0)\delta_0 + g$, where δ 0 is the Kronecker delta function and ![]() $g(0) = 0$. Let
$g(0) = 0$. Let ![]() $x = f(0)$ and
$x = f(0)$ and ![]() $y = \|g\|_{4/3}$. Since
$y = \|g\|_{4/3}$. Since ![]() $\|f\|_{4/3}=1$, we have
$\|f\|_{4/3}=1$, we have
From (4.8), we have
In particular, we have ![]() $y/x \leq 0.01$. Since
$y/x \leq 0.01$. Since ![]() $f*f = x^2\delta_0 + 2xg + g*g$, we have
$f*f = x^2\delta_0 + 2xg + g*g$, we have
 \begin{equation*} \|f*f\|_2 \leq x\|x\delta_0 + 2g\|_2 + \|g*g\|_2 = x \sqrt{\|x\delta_0\|_2^2 + \|2g\|_2^2} + \|g*g\|_2. \end{equation*}
\begin{equation*} \|f*f\|_2 \leq x\|x\delta_0 + 2g\|_2 + \|g*g\|_2 = x \sqrt{\|x\delta_0\|_2^2 + \|2g\|_2^2} + \|g*g\|_2. \end{equation*} Using the inequalities ![]() $\|g\|_2 \leq \|g\|_{4/3} = y$ and
$\|g\|_2 \leq \|g\|_{4/3} = y$ and  $\|g*g\|_2 \leq \|g\|_{4/3}^2 = y^2$, we obtain
$\|g*g\|_2 \leq \|g\|_{4/3}^2 = y^2$, we obtain
 \begin{equation*} \|f*f\|_2 \leq x\sqrt{x^2 + 4y^2} + y^2 = x^2 \sqrt{1 + \frac{4y^2}{x^2}} + y^2. \end{equation*}
\begin{equation*} \|f*f\|_2 \leq x\sqrt{x^2 + 4y^2} + y^2 = x^2 \sqrt{1 + \frac{4y^2}{x^2}} + y^2. \end{equation*} Since ![]() $\sqrt{1+\lambda} \leq 1 + \lambda/2$ for
$\sqrt{1+\lambda} \leq 1 + \lambda/2$ for ![]() $\lambda \geq 0$, it follows that
$\lambda \geq 0$, it follows that
 \begin{equation*} \|f*f\|_2 \leq x^2\left(1 + \frac{2y^2}{x^2}\right) + y^2 = x^2 + 3y^2. \end{equation*}
\begin{equation*} \|f*f\|_2 \leq x^2\left(1 + \frac{2y^2}{x^2}\right) + y^2 = x^2 + 3y^2. \end{equation*}On the other hand, note that
 \begin{equation*} \|f\|_q = (x^q + \|g\|_q^q)^{1/q}. \end{equation*}
\begin{equation*} \|f\|_q = (x^q + \|g\|_q^q)^{1/q}. \end{equation*}Since g is supported on a set of size n, by Hölder’s inequality, we have
 \begin{equation*} \|g\|_{4/3} \leq n^{3/4 - 1/q} \|g\|_q = (1+\delta)^{1/4} \|g\|_q. \end{equation*}
\begin{equation*} \|g\|_{4/3} \leq n^{3/4 - 1/q} \|g\|_q = (1+\delta)^{1/4} \|g\|_q. \end{equation*} By choosing δ > 0 to be small enough, we have  $\|g\|_q^q \geq 0.9 \|g\|_{4/3}^q = 0.9y^q$, and hence,
$\|g\|_q^q \geq 0.9 \|g\|_{4/3}^q = 0.9y^q$, and hence,
 \begin{equation*} \|f\|_q^2 \geq (x^q + 0.9y^q)^{2/q} = x^2\left(1 + \frac{0.9y^q}{x^q}\right)^{2/q}. \end{equation*}
\begin{equation*} \|f\|_q^2 \geq (x^q + 0.9y^q)^{2/q} = x^2\left(1 + \frac{0.9y^q}{x^q}\right)^{2/q}. \end{equation*} Since ![]() $4/3 \leq q \leq 3/2$, we have
$4/3 \leq q \leq 3/2$, we have ![]() $(1+\lambda)^{2/q} \geq 1+\lambda \geq 1+4\lambda^{2/q}$ for
$(1+\lambda)^{2/q} \geq 1+\lambda \geq 1+4\lambda^{2/q}$ for ![]() $0 \leq \lambda \leq 1/64$. Hence,
$0 \leq \lambda \leq 1/64$. Hence,
 \begin{equation*} \|f\|_q^2 \geq x^2\left(1 + 4 \cdot 0.9^{2/q} \cdot \frac{y^2}{x^2}\right) \geq x^2 + 3y^2. \end{equation*}
\begin{equation*} \|f\|_q^2 \geq x^2\left(1 + 4 \cdot 0.9^{2/q} \cdot \frac{y^2}{x^2}\right) \geq x^2 + 3y^2. \end{equation*} It follows that  $\|f*f\|_2 \leq \|f\|_q^2$, as desired.
$\|f*f\|_2 \leq \|f\|_q^2$, as desired.
5. Proof of theorem 1.2
Let ![]() $n \geq 3$ be a positive integer and let I be the interval
$n \geq 3$ be a positive integer and let I be the interval
 \begin{equation*} I = \left\{-\Bigl\lfloor \frac{n-1}{2}\Bigr\rfloor, \cdots, \Bigl\lfloor \frac{n}{2}\Bigr\rfloor\right\}, \end{equation*}
\begin{equation*} I = \left\{-\Bigl\lfloor \frac{n-1}{2}\Bigr\rfloor, \cdots, \Bigl\lfloor \frac{n}{2}\Bigr\rfloor\right\}, \end{equation*} which has length n. In view of proposition 2.1, it suffices to construct a function ![]() $f: I \rightarrow \mathbb{R}$ such that
$f: I \rightarrow \mathbb{R}$ such that  $|\widehat{f}\|_4 \gt \|f\|_q$, where
$|\widehat{f}\|_4 \gt \|f\|_q$, where
 \begin{equation*} q = \frac{4}{\log_n \frac{2n^3+n}{3}}. \end{equation*}
\begin{equation*} q = \frac{4}{\log_n \frac{2n^3+n}{3}}. \end{equation*} We take ![]() $f = 1_I + \varepsilon\delta_0$ for some small ɛ > 0, where δ 0 is the Kronecker delta function. Note that
$f = 1_I + \varepsilon\delta_0$ for some small ɛ > 0, where δ 0 is the Kronecker delta function. Note that  $\|\widehat{1_I}\|_4 = \|1_I\|_q$, and we will show that the small adjustment from 1I to f swings the inequality in the desired direction.
$\|\widehat{1_I}\|_4 = \|1_I\|_q$, and we will show that the small adjustment from 1I to f swings the inequality in the desired direction.
First note that
 \begin{equation*} \|f\|_q^q = n-1 + (1+\varepsilon)^q = n + q\varepsilon + O(\varepsilon^2). \end{equation*}
\begin{equation*} \|f\|_q^q = n-1 + (1+\varepsilon)^q = n + q\varepsilon + O(\varepsilon^2). \end{equation*}Hence,
 \begin{equation*} \|f\|_q^4 = n^{4/q} \left(1 + \frac{q\varepsilon}{n} + O\left(\frac{\varepsilon^2}{n}\right)\right)^{4/q} = n^{4/q} \left(1 + \frac{4\varepsilon}{n} + O\left(\frac{\varepsilon^2}{n}\right)\right). \end{equation*}
\begin{equation*} \|f\|_q^4 = n^{4/q} \left(1 + \frac{q\varepsilon}{n} + O\left(\frac{\varepsilon^2}{n}\right)\right)^{4/q} = n^{4/q} \left(1 + \frac{4\varepsilon}{n} + O\left(\frac{\varepsilon^2}{n}\right)\right). \end{equation*} Since ![]() $n^{4/q} = (2n^3+n)/3$, it follows that
$n^{4/q} = (2n^3+n)/3$, it follows that
 \begin{equation}
\|f\|_q^4 = \frac{1}{3}(2n^3+n) + \frac{4}{3}(2n^2+1)\varepsilon + O(n^2\varepsilon^2).
\end{equation}
\begin{equation}
\|f\|_q^4 = \frac{1}{3}(2n^3+n) + \frac{4}{3}(2n^2+1)\varepsilon + O(n^2\varepsilon^2).
\end{equation}Now consider the convolution
We have
 \begin{equation*}
\begin{split}
\|f*f\|_2^2 &= \sum_{a \notin I} 1_I*1_I(a)^2 + \sum_{a \in I\setminus \{0\}} (1_I*1_I(a) + 2\varepsilon)^2 + (1_I*1_I(0) + 2\varepsilon + \varepsilon^2)^2 \\
&= \sum_{a \notin I} 1_I*1_I(a)^2 + \sum_{a \in I} (1_I*1_I(a) + 2\varepsilon)^2 + O(n\varepsilon^2) \\
&= \sum_{a \in \mathbb{Z}} 1_I*1_I(a)^2 + 4\varepsilon \sum_{a \in I} 1_I*1_I(a) + O(n\varepsilon^2).
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\|f*f\|_2^2 &= \sum_{a \notin I} 1_I*1_I(a)^2 + \sum_{a \in I\setminus \{0\}} (1_I*1_I(a) + 2\varepsilon)^2 + (1_I*1_I(0) + 2\varepsilon + \varepsilon^2)^2 \\
&= \sum_{a \notin I} 1_I*1_I(a)^2 + \sum_{a \in I} (1_I*1_I(a) + 2\varepsilon)^2 + O(n\varepsilon^2) \\
&= \sum_{a \in \mathbb{Z}} 1_I*1_I(a)^2 + 4\varepsilon \sum_{a \in I} 1_I*1_I(a) + O(n\varepsilon^2).
\end{split}
\end{equation*}One can compute that
 \begin{equation*} \sum_{a \in \mathbb{Z}}1_I*1_I(a)^2 = E(I) = \frac{1}{3}(2n^3+n) \end{equation*}
\begin{equation*} \sum_{a \in \mathbb{Z}}1_I*1_I(a)^2 = E(I) = \frac{1}{3}(2n^3+n) \end{equation*}and
 \begin{equation*} \sum_{a \in I}1_I*1_I(a) = \Bigl\lceil \frac{3n^2}{4}\Bigr\rceil \geq \frac{3n^2}{4}. \end{equation*}
\begin{equation*} \sum_{a \in I}1_I*1_I(a) = \Bigl\lceil \frac{3n^2}{4}\Bigr\rceil \geq \frac{3n^2}{4}. \end{equation*}Hence,
 \begin{equation}
\|f*f\|_2^2 \geq \frac{1}{3}(2n^3+n) + 3n^2\varepsilon + O(n\varepsilon^2).
\end{equation}
\begin{equation}
\|f*f\|_2^2 \geq \frac{1}{3}(2n^3+n) + 3n^2\varepsilon + O(n\varepsilon^2).
\end{equation}Comparing (5.1) with (5.2) and noting that
 \begin{equation*} 3n^2 \gt \frac{4}{3}(2n^2+1) \end{equation*}
\begin{equation*} 3n^2 \gt \frac{4}{3}(2n^2+1) \end{equation*} for every ![]() $n \geq 3$, we conclude that
$n \geq 3$, we conclude that
 \begin{equation*} \|f*f\|_2^2 \gt \|f\|_q^4 \end{equation*}
\begin{equation*} \|f*f\|_2^2 \gt \|f\|_q^4 \end{equation*}for sufficiently small ɛ > 0. This completes the proof.