Article contents
Twists and shear maps in nonlinear elasticity: explicit solutions and vanishing Jacobians
Published online by Cambridge University Press: 23 January 2019
Abstract
In this paper we study constrained variational problems that are principally motivated by nonlinear elasticity theory. We examine, in particular, the relationship between the positivity of the Jacobian det ∇u and the uniqueness and regularity of energy minimizers u that are either twist maps or shear maps. We exhibit explicit twist maps, defined on two-dimensional annuli, that are stationary points of an appropriate energy functional and whose Jacobian vanishes on a set of positive measure in the annulus. Within the class of shear maps we precisely characterize the unique global energy minimizer 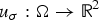 $u_{\sigma }: \Omega \to {\open R}^2$ in a model, two-dimensional case. We exploit the Jacobian constraint
$u_{\sigma }: \Omega \to {\open R}^2$ in a model, two-dimensional case. We exploit the Jacobian constraint 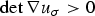 $\det \nabla u_{\sigma} \gt 0$ a.e. to obtain regularity results that apply ‘up to the boundary’ of domains with corners. It is shown that the unique shear map minimizer has the properties that (i)
$\det \nabla u_{\sigma} \gt 0$ a.e. to obtain regularity results that apply ‘up to the boundary’ of domains with corners. It is shown that the unique shear map minimizer has the properties that (i) 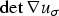 $\det \nabla u_{\sigma }$ is strictly positive on one part of the domain Ω, (ii)
$\det \nabla u_{\sigma }$ is strictly positive on one part of the domain Ω, (ii) 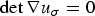 $\det \nabla u_{\sigma } = 0$ necessarily holds on the rest of Ω, and (iii) properties (i) and (ii) combine to ensure that
$\det \nabla u_{\sigma } = 0$ necessarily holds on the rest of Ω, and (iii) properties (i) and (ii) combine to ensure that 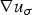 $\nabla u_{\sigma }$ is not continuous on the whole domain.
$\nabla u_{\sigma }$ is not continuous on the whole domain.
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 1 , February 2020 , pp. 41 - 71
- Copyright
- Copyright © Royal Society of Edinburgh 2019
References
- 2
- Cited by

