Article contents
Symmetrized and non-symmetrized asymptotic mean value Laplacian in metric measure spaces
Published online by Cambridge University Press: 28 November 2023
Abstract
The asymptotic mean value Laplacian—AMV Laplacian—extends the Laplace operator from $\mathbb {R}^n$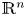 to metric measure spaces through limits of averaging integrals. The AMV Laplacian is however not a symmetric operator in general. Therefore, we consider a symmetric version of the AMV Laplacian, and focus lies on when the symmetric and non-symmetric AMV Laplacians coincide. Besides Riemannian and 3D contact sub-Riemannian manifolds, we show that they are identical on a large class of metric measure spaces, including locally Ahlfors regular spaces with suitably vanishing distortion. In addition, we study the context of weighted domains of $\mathbb {R}^n$
to metric measure spaces through limits of averaging integrals. The AMV Laplacian is however not a symmetric operator in general. Therefore, we consider a symmetric version of the AMV Laplacian, and focus lies on when the symmetric and non-symmetric AMV Laplacians coincide. Besides Riemannian and 3D contact sub-Riemannian manifolds, we show that they are identical on a large class of metric measure spaces, including locally Ahlfors regular spaces with suitably vanishing distortion. In addition, we study the context of weighted domains of $\mathbb {R}^n$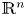 —where the two operators typically differ—and provide explicit formulae for these operators, including points where the weight vanishes.
—where the two operators typically differ—and provide explicit formulae for these operators, including points where the weight vanishes.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 155 , Issue 3 , June 2025 , pp. 916 - 953
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 1
- Cited by


