Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Feireisl, Eduard
1991.
A note on uniqueness for parabolic problems with discontinuous nonlinearities.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 16,
Issue. 11,
p.
1053.
Feireisl, Eduard
and
Norbury, John
1993.
A Comparison Theorem for a Nonlinear system Arising in Porous Medium Combustion.
Applicable Analysis,
Vol. 49,
Issue. 3-4,
p.
247.
Cardinali, Tiziana
Fiacca, Antonella
and
Papageorgiou, Nikolaos S.
1997.
Extremal solutions for nonlinear parabolic problems with discontinuities.
Monatshefte f�r Mathematik,
Vol. 124,
Issue. 2,
p.
119.
Díaz, Jesús Ildefonso
1997.
The Mathematics of Models for Climatology and Environment.
p.
217.
Kandilakis, Dimitrios A.
and
Papageorgiou, Nikolaos S.
1998.
Nonlinear periodic parabolic problems with nonmonotone discontinuities.
Proceedings of the Edinburgh Mathematical Society,
Vol. 41,
Issue. 1,
p.
117.
Valero, José
2001.
Attractors of Parabolic Equations Without Uniqueness.
Journal of Dynamics and Differential Equations,
Vol. 13,
Issue. 4,
p.
711.
2002.
Nonlinear Partial Differential Equations and their Applications - Collège de France Seminar Volume XIV.
Vol. 31,
Issue. ,
p.
297.
ARRIETA, JOSÉ M.
RODRÍGUEZ-BERNAL, ANÍBAL
and
VALERO, JOSÉ
2006.
DYNAMICS OF A REACTION–DIFFUSION EQUATION WITH A DISCONTINUOUS NONLINEARITY.
International Journal of Bifurcation and Chaos,
Vol. 16,
Issue. 10,
p.
2965.
Díaz, Jesus Ildefonso
and
Shmarev, Sergey
2009.
Lagrangian Approach to the Study of Level Sets: Application to a Free Boundary Problem in Climatology.
Archive for Rational Mechanics and Analysis,
Vol. 194,
Issue. 1,
p.
75.
Deguchi, Hideo
2009.
Existence, uniqueness and stability of weak solutions of parabolic systems with discontinuous nonlinearities.
Monatshefte für Mathematik,
Vol. 156,
Issue. 3,
p.
211.
BALIBREA, F.
CARABALLO, T.
KLOEDEN, P. E.
and
VALERO, J.
2010.
RECENT DEVELOPMENTS IN DYNAMICAL SYSTEMS: THREE PERSPECTIVES.
International Journal of Bifurcation and Chaos,
Vol. 20,
Issue. 09,
p.
2591.
Coti Zelati, Michele
Frémond, Michel
Temam, Roger
and
Tribbia, Joseph
2013.
The equations of the atmosphere with humidity and saturation: Uniqueness and physical bounds.
Physica D: Nonlinear Phenomena,
Vol. 264,
Issue. ,
p.
49.
Coti Zelati, Michele
2013.
On the Theory of Global Attractors and Lyapunov Functionals.
Set-Valued and Variational Analysis,
Vol. 21,
Issue. 1,
p.
127.
Gluzman, Mark O.
Gorban, Nataliia V.
and
Kasyanov, Pavlo O.
2015.
Lyapunov type functions for classes of autonomous parabolic feedback control problems and applications.
Applied Mathematics Letters,
Vol. 39,
Issue. ,
p.
19.
Temam, Roger
and
Wu, Kakuen John
2015.
Formulation of the equations of the humid atmosphere in the context of variational inequalities.
Journal of Functional Analysis,
Vol. 269,
Issue. 7,
p.
2187.
Gluzman, Mark O.
Gorban, Nataliia V.
and
Kasyanov, Pavlo O.
2015.
Continuous and Distributed Systems II.
Vol. 30,
Issue. ,
p.
233.
Temam, Roger
and
Wang, Xiaoyan
2016.
System Modeling and Optimization.
Vol. 494,
Issue. ,
p.
21.
Gorban, Nataliia V.
Gluzman, Mark O.
Kasyanov, Pavlo O.
and
Tkachuk, Alla M.
2016.
Advances in Dynamical Systems and Control.
Vol. 69,
Issue. ,
p.
351.
Valero, José
and
Simsen, Jacson
2016.
Global attractors for $p$-Laplacian differential inclusions in unbounded domains.
Discrete and Continuous Dynamical Systems - Series B,
Vol. 21,
Issue. 9,
p.
3239.
V. Gorban, Nataliia
V. Khomenko, Olha
S. Paliichuk, Liliia
and
M. Tkachuk, Alla
2017.
Long-time behavior of state functions for climate energy balance model.
Discrete & Continuous Dynamical Systems - B,
Vol. 22,
Issue. 5,
p.
1887.
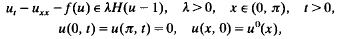
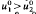 for any x ≠ 0, implies u1(t)>u2(t), t≧0 for any u1, u2 solving the problem with the initial data
for any x ≠ 0, implies u1(t)>u2(t), t≧0 for any u1, u2 solving the problem with the initial data 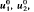 , respectively.
, respectively.
