For decreasing sequences $\{t_{n}\}_{n=1}^{\infty }$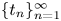 converging to zero and initial data $f\in H^s(\mathbb {R}^N)$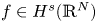, $N\geq 2$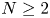, we consider the almost everywhere convergence problem for sequences of Schrödinger means ${\rm e}^{it_{n}\Delta }f$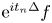, which was proposed by Sjölin, and was open until recently. In this paper, we prove that if $\{t_n\}_{n=1}^{\infty }$ 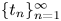belongs to Lorentz space ${\ell }^{r,\infty }(\mathbb {N})$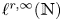, then the a.e. convergence results hold for $s>\min \{\frac {r}{\frac {N+1}{N}r+1},\,\frac {N}{2(N+1)}\}$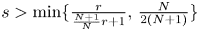. Inspired by the work of Lucà-Rogers, we construct a counterexample to show that our a.e. convergence results are sharp (up to endpoints). Our results imply that when $0< r<\frac {N}{N+1}$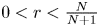, there is a gain over the a.e. convergence result from Du-Guth-Li and Du-Zhang, but not when $r\geq \frac {N}{N+1}$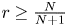, even though we are in the discrete case. Our approach can also be applied to get the a.e. convergence results for the fractional Schrödinger means and nonelliptic Schrödinger means.