Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-25T19:54:56.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Series expansion of Leray–Trudinger inequality

Part of: Elliptic equations and systems Real functions: Miscellaneous topics Inequalities

Published online by Cambridge University Press:  20 December 2021

Xiaomei Sun ,
Kaixiang Yu  and
Anqiang Zhu
Xiaomei Sun
Affiliation:
College of Science, Huazhong Agricultural University, Wuhan 430070, China (xmsunn@mail.hzau.edu.cn, ericykx@163.com)
Kaixiang Yu
Affiliation:
College of Science, Huazhong Agricultural University, Wuhan 430070, China (xmsunn@mail.hzau.edu.cn, ericykx@163.com)
Anqiang Zhu
Affiliation:
School of Mathematics and Statistics, Wuhan University, Wuhan 430070, China (aqzhu.math@whu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we establish an infinite series expansion of Leray–Trudinger inequality, which is closely related with Hardy inequality and Moser Trudinger inequality. Our result extends early results obtained by Mallick and Tintarev [A. Mallick and C. Tintarev. An improved Leray-Trudinger inequality. Commun. Contemp. Math. 20 (2018), 17501034. OP 21] to the case with many logs. It should be pointed out that our result is about series expansion of Hardy inequality under the case $p=n$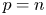, which case is not considered by Gkikas and Psaradakis in [K. T. Gkikas and G. Psaradakis. Optimal non-homogeneous improvements for the series expansion of Hardy's inequality. Commun. Contemp. Math. doi:10.1142/S0219199721500310]. However, we can't obtain the optimal form by our method.

Keywords

Leray–Trudinger inequalityseries expansionimproved Hardy inequality

MSC classification

Primary: 26D15: Inequalities for sums, series and integrals
Secondary: 26E10: $C^infty$-functions, quasi-analytic functions 35J20: Variational methods for second-order elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 1 , February 2023 , pp. 262 - 274
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adimurthi, S. F. and Tertikas, A.. on the best constant of Hardy-Sobolev inequalities. Nonlinear Anal. 70 (2009), 2826–2833.CrossRefGoogle Scholar
Adimurthi, N. C. and Ramaswamy, M.. An improved Hardy-Sobolev inequality and its application. Proc. Amer. Math. Soc. 130 (2002), 489–505.CrossRefGoogle Scholar
Adimurthi, K. S.. Existence and non-existence of the first eigenvalue of the perturbed Hardy-Sobolev operator. Proc. Roy. Soc. Edinburgh Sect. A 132 (2002), 1021–1043.CrossRefGoogle Scholar
Barbatis, G., Filippas, S. and Tertikas, A.. A unified approach to improved $L_p$ Hardy inequalities with best constants. Trans. Amer. Math. Soc. 356 (2004), 2169–2196.CrossRefGoogle Scholar
Barbatis, G., Filippas, S. and Tertikas, A.. Series expansion for $L_p$ Hardy inequalities. Indiana Univ. Math. J. 52 (2003), 171–190.Google Scholar
Brezis, H. and Marcus, M.. Hardy's inequalities revisited. Ann. Scuola. Norm. Sup. Pisa Cl. Sci. 25 (1997), 217–237.Google Scholar
Brezis, H., Marcus, M. and Shafrir, I.. Extremal functions for Hardy's inequality with weight. J. Funct. Anal. 171 (2000), 177–191.CrossRefGoogle Scholar
Brezis, H. and Vazquez, J. L.. Blow-up solutions of some nonlinear elliptic problems. Rev. Mat. Univ. Complut. Madrid 10 (1997), 443–469.Google Scholar
Chaudhuri, N. and Ramaswamy, M.. Existence of positive solutions of some semilinear elliptic equations with singular coefficients. Proc. Roy. Soc. Edinburgh Sect. A 131 (2001), 1275–1295.CrossRefGoogle Scholar
Davies, E. B.. A review of Hardy inequalities. Oper. Theory Adv. Appl. 110 (1999), 55–67.Google Scholar
Filippas, S. and Tertikas, A.. Optimizing improved Hardy inequalities. J. Funct. Anal. 192 (2002), 186–233.CrossRefGoogle Scholar
Gazzola, F., Grunau, H. C. and Mitidieri, E.. Hardy inequalities with optimal constants and remainder terms. Trans. Amer. Math. Soc. 356 (2004), 2149–2168.CrossRefGoogle Scholar
Gkikas, K. T. and Psaradakis, G.. Optimal non-homogeneous improvements for the series expansion of Hardy's inequality. Commun. Contemp. Math. doi:10.1142/S0219199721500310Google Scholar
Gilbarg, D. and Trudinger, N. S.. Elliptic partial differential equations of second order, (Springer-Verlag, Berlin, 2001).CrossRefGoogle Scholar
Hardy, G., Littlewood, J. E. and Pólya, G.. Inequalities (Cambridge University Press, Cambridge, 1952).Google Scholar
Leray, J.. Étude de diverses équations intégrales non linéaires et de quelques problèmes que pose l'hydrodynamique. J. Math. Pures Appl. 12 (1933), 1–82.Google Scholar
Li, Y. and Ruf, B.. A sharp Trudinger-Moser type inequality for unbounded domains in $\mathbb {R}^{n}$. Indiana Univ. Math. J. 57 (2008), 451–480.CrossRefGoogle Scholar
Moser, J.. A sharp form of an inequality by N. Trudinger. Indiana Univ. Math. J. 20 (1971), 1077–1092.CrossRefGoogle Scholar
Mallick, A. and Tintarev, C.. An improved Leray-Trudinger inequality. Commun. Contemp. Math. 20 (2018), 17501034.CrossRefGoogle Scholar
Opic, B. and Kufner, A., Hardy-type inequalities, Pitman Research Notes in Mathematics series, Volume 219 (Longman Scientific and Technical, Harlow, 1990).Google Scholar
Psaradakis, G. and Spector, D.. A Leray-Trudinger inequality. J. Funct. Anal. 269 (2015), 215–228.CrossRefGoogle Scholar
Ruf, B.. A sharp Trudinger-Moser type inequality for unbounded domains in $\mathbb {R}^{2}$. J. Funct. Anal. 219 (2005), 340–367.CrossRefGoogle Scholar
Tintarev, C.. Trudinger-Moser inequality with remainder terms. J. Funct. Anal. 266 (2014), 55–66.CrossRefGoogle Scholar
Vazquez, J. L. and Zuazua, E.. The Hardy inequality and the asymptotic behaviour of the heat equation with an inverse-square potential. J. Funct. Anal. 173 (2000), 103–153.CrossRefGoogle Scholar