No CrossRef data available.
Article contents
On the essential spectrum of self-adjoint operators
Published online by Cambridge University Press: 14 November 2011
Synopsis
We provide estimates of the form
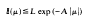
for the length of gap centre μ in the essential spectrum of a self-adjoint operator generated by a matrix differential expression.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 86 , Issue 3-4 , 1980 , pp. 261 - 274
- Copyright
- Copyright © Royal Society of Edinburgh 1980
References
1Eastham, M. S. P.. The spectral theory of periodic differential equations (Edinburgh: Scottish Academic Press, 1973).Google Scholar
2Eastham, M. S. P.. Asymptotic estimates for the lengths of the gaps in the essential spectrum of self-adjoint differential operators. Proc. Roy. Soc. Edinburgh Sect. A 74 (1976), 239–252.Google Scholar
3Eastham, M. S. P.. Gaps in the essential spectrum of even order self-adjoint operators. Proc. London Math. Soc. 32 (1976), 213–230.Google Scholar
4Feigin, V. I.. The continuous spectrum of differential operators. Functional Anal. Appl. (1), 11 (1977), 35–44.CrossRefGoogle Scholar
5Harris, B. J.. A systematic method of estimating gaps in the essential spectrum of self-adjoint operators. J. London Math. Soc. 18 (1978), 115–132.CrossRefGoogle Scholar
6Harris, B. J.. Gaps in the essential spectra of Schrödinger and Dirac operators. J. London Math. Soc., 18 (1978), 489–502.CrossRefGoogle Scholar
7Harris, B. J.. On the spectra and stability of periodic differential equations. Proc. London Math. Soc., to appear.Google Scholar
8Lazutkin, V. F., and Pankratova, T. F.. Asymptotics of the width of gaps in the spectrum of a Sturm-Liouville operator with periodic potential. Soviet Math. Dokl. 15 (1974), 649–653.Google Scholar
9Simonyan, S. G.. Asymptotic properties of the width of gaps in the spectrum of a Sturm-Liouville operator with periodic analytic potential. Differential Equations 6 (1970), 965–71.Google Scholar
10Weidmann, J.. Oscillationmethoden für systeme gewöhnlicher Differentialgleichungen. Math. Z. 119 (1971), 349–373.CrossRefGoogle Scholar

