Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gou, Tianxiang
and
Jeanjean, Louis
2018.
Multiple positive normalized solutions for nonlinear Schrödinger systems.
Nonlinearity,
Vol. 31,
Issue. 5,
p.
2319.
Noris, Benedetta
Tavares, Hugo
and
Verzini, Gianmaria
2019.
Normalized solutions for nonlinear Schrödinger systems on bounded domains.
Nonlinearity,
Vol. 32,
Issue. 3,
p.
1044.
Bonheure, Denis
Casteras, Jean-Baptiste
Gou, Tianxiang
and
Jeanjean, Louis
2019.
Normalized solutions to the mixed dispersion nonlinear Schrödinger equation in the mass critical and supercritical regime.
Transactions of the American Mathematical Society,
Vol. 372,
Issue. 3,
p.
2167.
Soave, Nicola
2020.
Normalized ground states for the NLS equation with combined nonlinearities.
Journal of Differential Equations,
Vol. 269,
Issue. 9,
p.
6941.
Soave, Nicola
2020.
Normalized ground states for the NLS equation with combined nonlinearities: The Sobolev critical case.
Journal of Functional Analysis,
Vol. 279,
Issue. 6,
p.
108610.
Bartsch, Thomas
Liu, Yanyan
and
Liu, Zhaoli
2020.
Normalized solutions for a class of nonlinear Choquard equations.
SN Partial Differential Equations and Applications,
Vol. 1,
Issue. 5,
Xie, Weihong
Chen, Haibo
and
Shi, Hongxia
2020.
Existence and multiplicity of normalized solutions for a class of Schrödinger‐Poisson equations with general nonlinearities.
Mathematical Methods in the Applied Sciences,
Vol. 43,
Issue. 6,
p.
3602.
Feng, Binhua
Ren, Jiajia
and
Wang, Qingxuan
2020.
Existence and instability of normalized standing waves for the fractional Schrödinger equations in the L2-supercritical case.
Journal of Mathematical Physics,
Vol. 61,
Issue. 7,
Luo, Haijun
and
Zhang, Zhitao
2020.
Normalized solutions to the fractional Schrödinger equations with combined nonlinearities.
Calculus of Variations and Partial Differential Equations,
Vol. 59,
Issue. 4,
Lu, Lu
2020.
L2normalized solutions for nonlinear Schrödinger systems inR3.
Nonlinear Analysis,
Vol. 191,
Issue. ,
p.
111621.
Binhua, Feng
Chen, Ruipeng
and
Liu, Jiayin
2020.
Blow-up criteria and instability of normalized standing waves for the fractional Schrödinger-Choquard equation.
Advances in Nonlinear Analysis,
Vol. 10,
Issue. 1,
p.
311.
Li, Meng
He, Jinchun
Xu, Haoyuan
and
Yang, Meihua
2020.
Normalized solutions for a coupled fractional Schrödinger system in low dimensions.
Boundary Value Problems,
Vol. 2020,
Issue. 1,
Chen, Zhen
and
Zou, Wenming
2021.
Normalized solutions for nonlinear Schrödinger systems with linear couples.
Journal of Mathematical Analysis and Applications,
Vol. 499,
Issue. 1,
p.
125013.
Pellacci, Benedetta
Pistoia, Angela
Vaira, Giusi
and
Verzini, Gianmaria
2021.
Normalized concentrating solutions to nonlinear elliptic problems.
Journal of Differential Equations,
Vol. 275,
Issue. ,
p.
882.
Gou, Tianxiang
and
Zhang, Zhitao
2021.
Normalized solutions to the Chern-Simons-Schrödinger system.
Journal of Functional Analysis,
Vol. 280,
Issue. 5,
p.
108894.
Li, Houwang
and
Zou, Wenming
2021.
Normalized ground states for semilinear elliptic systems with critical and subcritical nonlinearities.
Journal of Fixed Point Theory and Applications,
Vol. 23,
Issue. 3,
Bartsch, Thomas
Zhong, Xuexiu
and
Zou, Wenming
2021.
Normalized solutions for a coupled Schrödinger system.
Mathematische Annalen,
Vol. 380,
Issue. 3-4,
p.
1713.
Yang, Zuo
2021.
Normalized ground state solutions for Kirchhoff type systems.
Journal of Mathematical Physics,
Vol. 62,
Issue. 3,
Bartsch, Thomas
Molle, Riccardo
Rizzi, Matteo
and
Verzini, Gianmaria
2021.
Normalized solutions of mass supercritical Schrödinger equations with potential.
Communications in Partial Differential Equations,
Vol. 46,
Issue. 9,
p.
1729.
He, Zhiqian
Feng, Binhua
and
Liu, Jiayin
2022.
Existence, stability and asymptotic behaviour of normalized solutions for the Davey-Stewartson system.
Discrete and Continuous Dynamical Systems,
Vol. 42,
Issue. 12,
p.
5937.
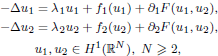
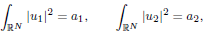
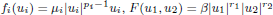 , with positive constants β, μi , pi , ri . The exponents are Sobolev subcritical but may be L 2-supercritical. Our main result deals with the case in which
, with positive constants β, μi , pi , ri . The exponents are Sobolev subcritical but may be L 2-supercritical. Our main result deals with the case in which 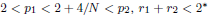 in dimensions 2 ≤ N ≤ 4. We also consider the cases in which all of these numbers are less than 2 + 4/N or all are bigger than 2 + 4/N.
in dimensions 2 ≤ N ≤ 4. We also consider the cases in which all of these numbers are less than 2 + 4/N or all are bigger than 2 + 4/N.
