Article contents
A Hilbert space approach to distributions
Published online by Cambridge University Press: 14 November 2011
Synopsis
A compact chain of Sobolev type Hilbert spaces 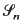 , n integer, is introduced that is invariant with
, n integer, is introduced that is invariant with
respect to the Fourier transform ℱ. The spaces 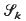 are related to powers of the adjoint of the so-called tempered derivative introduced in the sequential approach to distributions. It turns out that the intersection of all these Hilbert spaces coincides with the space of rapidly decaying C∞-functions and their union leads to the space of tempered distributions. Moreover, the naturally induced convergence concepts coincide with the usual ones. The approach provides not only a new and arguably more elementary approach to distributions it also provides a deeper insight into the action of the Fourier transform which is a unitary mapping in each space of the chain. Finally the Schwartz distributions are incorporated in the approach as locally tempered distributions.
are related to powers of the adjoint of the so-called tempered derivative introduced in the sequential approach to distributions. It turns out that the intersection of all these Hilbert spaces coincides with the space of rapidly decaying C∞-functions and their union leads to the space of tempered distributions. Moreover, the naturally induced convergence concepts coincide with the usual ones. The approach provides not only a new and arguably more elementary approach to distributions it also provides a deeper insight into the action of the Fourier transform which is a unitary mapping in each space of the chain. Finally the Schwartz distributions are incorporated in the approach as locally tempered distributions.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 115 , Issue 3-4 , 1990 , pp. 275 - 288
- Copyright
- Copyright © Royal Society of Edinburgh 1990
References
- 1
- Cited by

