Hostname: page-component-7dd5485656-j7khd Total loading time: 0 Render date: 2025-10-30T18:00:50.958Z Has data issue: false hasContentIssue false
  • English
  • Français

Global centres in a class of quintic polynomial differential systems

Part of: Qualitative theory

Published online by Cambridge University Press:  11 April 2024

Leonardo P. C. da Cruz Open the ORCID record for Leonardo P. C. da Cruz [Opens in a new window]  and
Jaume Llibre Open the ORCID record for Jaume Llibre [Opens in a new window]
Leonardo P. C. da Cruz
Affiliation:
Departamento de Matemática, Instituto de Ciências Matemáticas e Computação, Universidade de São Paulo, Avenida Trabalhador São Carlense, 400, 13566-590, São Carlos, SP, Brazil (leonardocruz@icmc.usp.br)
Jaume Llibre
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra, Barcelona, Catalonia, Spain (Jaume.Llibre@uab.cat)
Get access Rights & Permissions [Opens in a new window]

Abstract

A centre of a differential system in the plane $ {\mathbb {R}}^2$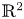 is an equilibrium point $p$ 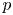having a neighbourhood $U$ 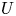such that $U\setminus \{p\}$ 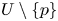is filled with periodic orbits. A centre $p$ 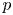is global when $ {\mathbb {R}}^2\setminus \{p\}$ 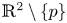is filled with periodic orbits. In general, it is a difficult problem to distinguish the centres from the foci for a given class of differential systems, and also it is difficult to distinguish the global centres inside the centres. The goal of this paper is to classify the centres and the global centres of the following class of quintic polynomial differential systems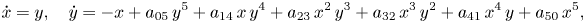

\begin{align*} \dot{x}= y,\quad \dot{y}={-}x+a_{05}\,y^5+a_{14}\,x\,y^4+a_{23}\,x^2\,y^3+a_{32}\,x^3\,y^2+a_{41}\,x^4\,y+a_{50}\,x^5, \end{align*}
in the plane $ {\mathbb {R}}^2$.

Keywords

centreglobal centrepolynomial differential systemsLyapunov quantitiesblow upquintic polynomial

MSC classification

Primary: 34C05: Location of integral curves, singular points, limit cycles

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 16
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adams, W. W. and Loustaunau, P., An introduction to Grobner bases, volume 3, Graduate Studies in Mathematics (American Mathematical Society, Providence, RI, 1994).CrossRefGoogle Scholar
Andronov, A. A., Leontovich, E. A., Gordon, I. I. and Maier, A. G., Qualitative theory of second-order dynamic systems. Israel Program for Scientific Translations (Halsted Press (A division of Wiley), New York, 1973).Google Scholar
Barreira, L., Llibre, J. and Valls, C.. Linear type global centers of cubic Hamiltonian systems symmetric with respect to the $x$-Axis. Electronic J. Differ. Equ. 57 (2020), 1–14.Google Scholar
Barreira, L., Llibre, J. and Valls, C.. On the global nilpotent centers of cubic polynomial Hamiltonian systems. Differ. Equ. Dyn. Syst. (2022).CrossRefGoogle Scholar
Blows, T. R. and Lloyd, N. G.. The number of limit cycles of certain polynomial differential equations. Proc. Roy. Soc. Edinburgh Sect. A 98 (1984), 215–239.CrossRefGoogle Scholar
Cima, A., Gasull, A. and Mañosas, F.. A note on the Lyapunov and period constants. Qual. Theory Dyn. Syst. 19 (2020), 1–13.CrossRefGoogle Scholar
Conti, R.. Centers of planar polynomial systems: a review. Le Math. LIII (1998), 207–240.Google Scholar
Cox, D., Little, J. and O'Shea, D., Ideals, varieties, and algorithms. Undergraduate Texts in Mathematics, 2nd edn (Springer-Verlag, New York, 1997).CrossRefGoogle Scholar
Decker, W., Greuel, G. M., Pfister, G. and Schönemann, H., Singular 4-1-1 – a computer algebra system for polynomial computations. http://www.singular.uni-kl.de, 2018.Google Scholar
Decker, W., Pfister, G., Schönemann, H. and Laplagne, S., primdec.lib a singular 4-1-1 library for computing the primary decomposition and radical ideals, 2018.Google Scholar
Dulac, H.. Détermination et intégration d'une certaine class d’équations différentialles ayant pour point singulier un centre. Bull. Sci. Math. 32 (1908), 230–252.Google Scholar
Dumortier, F., Llibre, J. and Artés, J. C., Qualitative theory of planar differential systems. UniversiText (Springer-Verlag, New York, 2006).Google Scholar
Frommer, M.. $\ddot {u}$ber das Auftreten von Wirbeln und Strudeln (geschlossener und spiraliger Integralkurven) in der Umgebung rationaler Unbestimmtheitsstellen. Math. Ann. 109 (1934), 395–424.CrossRefGoogle Scholar
Galeatti, M. and Villarini, M.. Some properties of planar polynomial systems of even degree. Ann. Mat. Pura Appl. 161 (1992), 299–313.CrossRefGoogle Scholar
García-Saldaña, J. D., Llibre, J. and Valls, C.. Linear type global centers of linear systems with cubic homogeneous nonlinearities. Rend. Circ. Mat. Palermo 69 (2020), 771–785.CrossRefGoogle Scholar
García-Saldaña, J. D., Llibre, J. and Valls, C.. Nilpotent global centers of linear systems with cubic homogeneous nonlinearities. Inter. J. Bifurcat. Chaos 30 (2020), 1–12.CrossRefGoogle Scholar
García-Saldaña, J. D., Llibre, J. and Valls, C.. On a class of global centers of linear systems with quintic homogeneous nonlinearities. Dyn. Cont. Discrete Impulsive Syst. 30 (2020), 135–148.Google Scholar
Gianni, P., Trager, B. and Zacharias, G.. Gröbner bases and primary decomposition of polynomial ideals. J. Symbolic Comput. 6 (1988), 149–167.CrossRefGoogle Scholar
Ilyashenko, Y. and Yakovenko, S., Lectures on analytic differential equations, volume 86 of Graduate Studies in Mathematics (American Mathematical Society, Providence, RI, 2008).CrossRefGoogle Scholar
Kaptyen, W.. On the midpoints of integral curves of differential equations of the first degree. Nederl. Adak. Wetecnsch. Verslag. Afd. Natuurk. Konikl. 0 (1911), 1446–1457.Google Scholar
Kaptyen, W.. New investigations on the midpoints of integral of differential equations of the first degree. Nederl. Adak. Wetecnsch. Verslag. Afd. Natuurk. Konikl. 20 (1912), 1354–1365.Google Scholar
Liapunov, A. M.. Investigation of one of the special cases of the stability of motion. Mat. Sb. 17 (1893), 253–333.Google Scholar
Liapunov, A. M., Probléme Général de la Stabilité du Mouvement. Annals of Mathematics Studies, Vol. 17 (Princeton University Press, Princeton, NJ, Oxford University Press, London, 1947).Google Scholar
Liapunov, A. M., Stability of motion. Mathematics in Science and Engineering, Vol. 30 (Academic Press, New York, London, 1966).Google Scholar
Llibre, J. and Valls, C.. Polynomial differential systems with even degree have no global centers. J. Math Anal. Appl. 503 (2021), 125–281.CrossRefGoogle Scholar
Llibre, J. and Valls, C.. Reversible global centers with quintic homogeneous nonlinearities. Dyn. Syst. 38 (2023), 1–22.CrossRefGoogle Scholar
Mac Lane, S. and Birkho, G.. Algebra (The Macmillan Company, Collier Macmillan Ltd, New York, London, 1967).Google Scholar
Poincaré, H., Mémoire sur les courbes définies par une équation différentielle. Sér. (3)7(1881), 375–422; Sér. (3)8: 251–296, 1882; Sér. (4)1. 167–244, 1882; Sér. (4)2: 151–217, 1886.Google Scholar
Romanovski, V. G. and Shafer, D. S.. The center and cyclicity problems: a computational algebra approach (Birkhäuser Boston Inc., Boston, MA, 2009).Google Scholar
Roussarie, R., Bifurcation of planar vector fields and Hilbert's sixteenth problem, Progress in Mathematics, Vol. 64 (Birkhäuser Verlag, Basel, 1998).CrossRefGoogle Scholar
Saharnikov, N. A.. On Frommer's conditions for the existence of a center. Akad. Nauk SSSR. Prikl. Mat. Meh. 12 (1948), 669–670.Google Scholar
Sibirskiĭ, K. S.. The principle of symmetry and the problem of the center. Kišinev. Gos. Univ. Uc. Zap. 17 (1955), 27–34.Google Scholar
Zoładek, H.. Quadratic systems with center and their perturbations. J. Differ. Equ. 109 (1994), 223–273.CrossRefGoogle Scholar