Hostname: page-component-857557d7f7-c8jtx Total loading time: 0 Render date: 2025-11-25T00:10:49.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite-time blow-up in a repulsive chemotaxis-consumption system

Part of: Partial differential equations Parabolic equations and systems Physiological, cellular and medical topics Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  06 June 2022

Yulan Wang  and
Michael Winkler
Yulan Wang
Affiliation:
School of Science, Xihua University, 610039 Chengdu, China (wangyulan-math@163.com)
Michael Winkler
Affiliation:
Institut für Mathematik, Universität Paderborn, 33098 Paderborn, Germany (michael.winkler@math.uni-paderborn.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

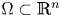In a ball $\Omega \subset \mathbb {R}^{n}$ with $n\ge 2$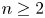, the chemotaxis system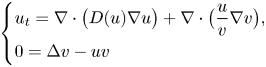

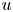\[ \left\{ \begin{array}{@{}l} u_t = \nabla \cdot \big( D(u)\nabla u\big) + \nabla\cdot \big(\dfrac{u}{v} \nabla v\big), \\ 0=\Delta v - uv \end{array} \right. \]
is considered along with no-flux boundary conditions for $u$ and with prescribed constant positive Dirichlet boundary data for $v$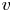. It is shown that if $D\in C^{3}([0,\infty ))$ 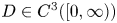is such that $0< D(\xi ) \le {K_D} (\xi +1)^{-\alpha }$ 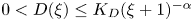for all $\xi >0$ 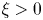with some ${K_D}>0$ 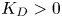and $\alpha >0$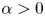, then for all initial data from a considerably large set of radial functions on $\Omega$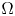, the corresponding initial-boundary value problem admits a solution blowing up in finite time.

Keywords

Chemotaxisconsumption mechanismfinite-time blow-up

MSC classification

Primary: 35K65: Degenerate parabolic equations
Secondary: 35B40: Asymptotic behavior of solutions 35Q92: PDEs in connection with biology and other natural sciences 92C17: Cell movement (chemotaxis, etc.)

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 4 , August 2023 , pp. 1150 - 1166
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Black, T.. Eventual smoothness of generalized solutions to a singular chemotaxis-Stokes system in 2D. J. Differ. Equ. 265 (2018), 2296–2339.CrossRefGoogle Scholar
Cao, X. and Lankeit, J.. Global classical small-data solutions for a three-dimensional chemotaxis Navier–Stokes system involving matrix-valued sensitivities. Calc. Var. Part. Differ. Equ. 55 (2016), 107.CrossRefGoogle Scholar
Cieślak, T., Morales Rodrigo, C. and Laurençot, Ph., Global existence and convergence to steady states in a chemorepulsion system. Parabolic and Navier–Stokes equations. Part 1, 105–117, Banach Center Publ. Vol. 81, Part 1 (Polish Acad. Sci. Inst. Math., Warsaw, 2008).Google Scholar
Cieślak, T. and Stinner, C.. Finite-time blowup and global-in-time unbounded solutions to a parabolic-parabolic quasilinear Keller–Segel system in higher dimensions. J. Differ. Equ. 252 (2012), 5832–5851.CrossRefGoogle Scholar
Cieślak, T. and Winkler, M.. Finite-time blow-up in a quasilinear system of chemotaxis. Nonlinearity 21 (2008), 1057–1076.Google Scholar
Duan, R. J., Lorz, A. and Markowich, P. A.. Global solutions to the coupled chemotaxis-fluid equations. Comm. Partial Differ. Equ. 35 (2010), 1635–1673.CrossRefGoogle Scholar
Espejo, E. and Wu, H.. Optimal critical mass for the two-dimensional Keller–Segel model with rotational flux terms. Commun. Math. Sci. 18 (2020), 379–394.Google Scholar
Herrero, M. A. and Velázquez, J. J. L.. A blow-up mechanism for a chemotaxis model. Ann. Scu. Norm. Sup. Pisa Cl. Sci. 24 (1997), 633–683.Google Scholar
Hillen, T. and Painter, K.. A user's guide to PDE models for chemotaxis. J. Math. Biol. 58 (2009), 183–217.CrossRefGoogle ScholarPubMed
Höfer, T., Sherratt, J. A. and Maini, P. K.. Dictyostelium discoideum: cellular self-organisation in an excitable biological medium. Proc. R. Soc. London B 259 (1995), 249–257.Google Scholar
Jäger, W. and Luckhaus, S.. On explosions of solutions to a system of partial differential equations modelling chemotaxis. Trans. Am. Math. Soc. 329 (1992), 819–824.Google Scholar
Jiang, J., Wu, H. and Zheng, S.. Global existence and asymptotic behavior of solutions to a chemotaxis-fluid system on general bounded domains. Asymptot. Anal. 92 (2015), 249–258.Google Scholar
Keller, E. F. and Segel, L. A.. Initiation of slime mold aggregation viewed as an instability. J. Theor. Biol. 26 (1970), 399–415.CrossRefGoogle ScholarPubMed
Lankeit, J. Locally bounded global solutions to a chemotaxis consumption model with singular sensitivity and nonlinear diffusion. J. Differ. Equ. 262 (2017), 4052–4084.Google Scholar
Lankeit, J. and Viglialoro, G.. Global existence and boundedness of solutions to a chemotaxis-consumption model with singular sensitivity. Acta Appl. Math. 167 (2020), 75–97.Google Scholar
Li, G. and Winkler, M., Relaxation in a Keller–Segel-consumption system involving signal-dependent motilities. Preprint.Google Scholar
Liu, D.. Global classical solution to a chemotaxis consumption model with singular sensitivity. Nonlinear Anal. Real World Appl. 41 (2018), 497–508.CrossRefGoogle Scholar
Liu, J. Large-time behavior in a two-dimensional logarithmic chemotaxis-Navier–Stokes system with signal absorption. J. Evol. Equ. 21 (2021), 5135–5170.CrossRefGoogle Scholar
Matsushita, M. and Fujikawa, H.. Diffusion-limited growth in bacterial colony formation. Phys. A. 168 (1990), 498–506.CrossRefGoogle Scholar
Nagai, T.. Blowup of nonradial solutions to parabolic-elliptic systems modeling chemotaxis in two-dimensional domains. J. Inequal. Appl. 6 (2001), 37–55.Google Scholar
Rosen, G.. Steady-state distribution of bacteria chemotactic toward oxygen. Bull. Math. Biol. 40 (1978), 671–674.CrossRefGoogle ScholarPubMed
Tao, Y.. Boundedness in a chemotaxis model with oxygen consumption by bacteria. J. Math. Anal. Appl. 381 (2011), 521–529.CrossRefGoogle Scholar
Tao, Y., Wang, L. H. and Wang, Z. A.. Large-time behavior of a parabolic-parabolic chemotaxis model with logarithmic sensitivity in one dimension. Discrete Contin. Dyn. Syst. Ser. B 18 (2013), 821–845.Google Scholar
Tao, Y. and Winkler, M.. Eventual smoothness and stabilization of large-data solutions in a three-dimensional chemotaxis system with consumption of chemoattractant. J. Differ. Equ. 252 (2012), 2520–2543.Google Scholar
Tuval, I., Cisneros, L., Dombrowski, C., Wolgemuth, C. W., Kessler, J. O. and Goldstein, R. E.. Bacterial swimming and oxygen transport near contact lines. Proc. Nat. Acad. Sci. USA 102 (2005), 2277–2282.CrossRefGoogle ScholarPubMed
Wang, Y., Winkler, M. and Xiang, Z.. Immediate regularization of measure-type population densities in a two-dimensional chemotaxis system with signal consumption. Sci. China Math. 64 (2021), 725–746.Google Scholar
Wang, Z. A., Xiang, Z. and Yu, P.. Asymptotic dynamics in a singular chemotaxis system modeling onset of tumor angiogenesis. J. Differ. Equ. 260 (2016), 2225–2258.CrossRefGoogle Scholar
Winkler, M. Finite-time blow-up in the higher-dimensional parabolic-parabolic Keller–Segel system. J. Math. Pures Appl. 100 (2013), 748–767. preprint arXiv:1112.4156v1.Google Scholar
Winkler, M.. Stabilization in a two-dimensional chemotaxis-Navier–Stokes system. Arch. Ration. Mech. Anal. 211 (2014), 455–487.CrossRefGoogle Scholar
Winkler, M.. Large-data global generalized solutions in a chemotaxis system with tensor-valued sensitivities. SIAM J. Math. Anal. 47 (2015), 3092–3115.CrossRefGoogle Scholar
Winkler, M.. How far do chemotaxis-driven forces influence regularity in the Navier–Stokes system?. Trans. Am. Math. Soc. 369 (2017), 3067–3125.CrossRefGoogle Scholar
Winkler, M. Can rotational fluxes impede the tendency toward spatial homogeneity in nutrient taxis(-Stokes) systems?. Int. Math. Res. Notices (2021). to appear https://doi.org/10.1093/imrn/rnz056.CrossRefGoogle Scholar
Winkler, M., Discovering unlimited growth in a chemotaxis-Navier–Stokes system via intermediate limits. Preprint.Google Scholar
Zhang, Q.. Boundedness in chemotaxis systems with rotational flux terms. Math. Nachr. 289 (2016), 2323–2334.Google Scholar
Zhang, Q. and Li, Y.. Stabilization and convergence rate in a chemotaxis system with consumption of chemoattractant J. Math. Phys. 56 (2015), 081506.CrossRefGoogle Scholar
Zhang, Q. and Li, Y.. Global weak solutions for the three-dimensional chemotaxis-Navier–Stokes system with nonlinear diffusion. J. Differ. Equ. 259 (2015), 3730–3754.CrossRefGoogle Scholar
Zhao, X. and Zheng, S.. Asymptotic behavior to a chemotaxis consumption system with singular sensitivity. Math. Meth. Appl. Sci. 41 (2018), 2615–2624.CrossRefGoogle Scholar
Zheng, J. and Wang, Y.. A note on global existence to a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant. Discrete Contin. Dyn. Syst. Ser. B 22 (2017), 669–686.Google Scholar