No CrossRef data available.
Article contents
Embeddings of non-simply-connected 4-manifolds in 7-space. II. On the smooth classification
Published online by Cambridge University Press: 22 January 2021
Abstract
We work in the smooth category. Let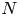 
$N$ be a closed connected orientable 4-manifold with torsion free 
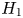$H_1$, where 
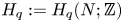$H_q := H_q(N; {\mathbb Z} )$. Our main result is a readily calculable classification of embeddings 
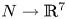$N \to {\mathbb R}^7$ up to isotopy, with an indeterminacy. Such a classification was only known before for 
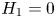$H_1=0$ by our earlier work from 2008. Our classification is complete when 
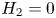$H_2=0$ or when the signature of 
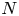$N$ is divisible neither by 64 nor by 9.
The group of knots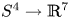 
$S^4\to {\mathbb R}^7$ acts on the set of embeddings 
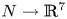$N\to {\mathbb R}^7$ up to isotopy by embedded connected sum. In Part I we classified the quotient of this action. The main novelty of this paper is the description of this action for 
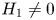$H_1 \ne 0$, with an indeterminacy.
Besides the invariants of Part I, detecting the action of knots involves a refinement of the Kreck invariant from our work of 2008.
For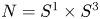 
$N=S^1\times S^3$ we give a geometrically defined 1–1 correspondence between the set of isotopy classes of embeddings and a certain explicitly defined quotient of the set 
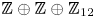${\mathbb Z} \oplus {\mathbb Z} \oplus {\mathbb Z} _{12}$.
MSC classification
Primary:
57R52: Isotopy
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 1 , February 2022 , pp. 163 - 181
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
Boechat, J. and Haefliger, A.. Plongements differentiables de varietes de dimension 4 dans 
${\mathbb R} ^7$. Essays on topology and related topics Springer, (1970), 156–166.CrossRefGoogle Scholar
${\mathbb R} ^7$. Essays on topology and related topics Springer, (1970), 156–166.CrossRefGoogle ScholarCencelj, M., Repovš, D. and Skopenkov, M.. Classification of knotted tori in the 2-metastable dimension. Mat. Sbornik 203 (2012), 1654–1681. arxiv:math/0811.2745.CrossRefGoogle Scholar
Crowley, D. and Skopenkov, A.. A classification of smooth embeddings of 4-manifolds in 7-space, II. Intern. J. Math. 22 (2011), 731–757. arxiv:math/0808.1795.CrossRefGoogle Scholar
Crowley, D. and Skopenkov, A.. Embeddings of non-simply-connected 4-manifolds in 7-space. I. Classification modulo knots. Moscow Math. J. to appear. arXiv:1611.04738.Google Scholar
Crowley, D. and Skopenkov, A.. Embeddings of non-simply-connected 4-manifolds in 7-space. II. On the smooth classification. arXiv:1612.04776.Google Scholar
Donaldson, S. K.. The orientation of Yang-Mills moduli spaces and 4-manifold topology. J. Diff. Geom. 26 (1987), 397–428.Google Scholar
* Gompf, R. and Stipsicz, A.. 4-Manifolds and Kirby Calculus (Providence, RI: American Mathematical Society, 1999).CrossRefGoogle Scholar
Kreck, M. and Stolz, S.. Some nondiffeomorphic homeomorphic homogeneous 7-manifolds with positive sectional curvature. J. Differ. Geom. 33 (1991), 465–486.Google Scholar
Levine, J.. Inertia groups of manifolds and diffeomorphisms of spheres. Amer. J. Math. 92 (1970), 243–258.CrossRefGoogle Scholar
Schultz, R.. Homotopy decompositions of equivariant function spaces. I. Math. Z. 131 (1973), 49–75.CrossRefGoogle Scholar
* Skopenkov, A.. Embedding and knotting of manifolds in Euclidean spaces. London Math. Soc. Lect. Notes 347 (2008), 248–342. arXiv:math/0604045.Google Scholar
Skopenkov, A.. Classification of smooth embeddings of 3-manifolds in 6-space. Math. Zeitschrift 260 (2008), 647–672. arxiv:math/0603429.CrossRefGoogle Scholar
Skopenkov, A.. A classification of smooth embeddings of 4-manifolds in 7-space, I. Topol. Appl. 157 (2010), 2094–2110. arxiv:math/0808.1795.CrossRefGoogle Scholar
Skopenkov, M.. When is the set of embeddings finite up to isotopy? Intern. J. Math. 26 (2015), 28 pp., arxiv:1106.1878.CrossRefGoogle Scholar
Skopenkov, A.. Classification of knotted tori. Proc. A of the Royal Society of Edinburgh 150 (2020), 549–567. Full version. arXiv:1502.04470.CrossRefGoogle Scholar
* Skopenkov, A.. Embeddings in Euclidean space: an introduction to their classification, to appear in Boll. Man. Atl. http://www.map.mpim-bonn.mpg.de/Embeddings_in_Euclidean_space:_an_introduction_to_their_classification.Google Scholar
* Skopenkov, A.. Embeddings just below the stable range: classification, to appear in Boll. Man. Atl. http://www.map.mpim-bonn.mpg.de/Embeddings_just_below_the_stable_range:_classification.Google Scholar
* Skopenkov, A.. 4-manifolds in 7-space, to appear in Boll. Man. Atl. http://www.map.mpim-bonn.mpg.de/4-manifolds_in_7-space.Google Scholar
* Skopenkov, A.. 3-manifolds in 6-space, to appear in Boll. Man. Atl. http://www.map.mpim-bonn.mpg.de/3-manifolds_in_6-space.Google Scholar
Viro, O. Y.. Local knotting of submanifolds (in Russian). Mat. Sbornik 90 (1973), 173–183.Google Scholar
Wall, C. T. C.. Classification problems in differential topology. V. On certain 6-manifolds. Invent. Math. 1 (1966), 355–374.CrossRefGoogle Scholar
Wilkens, D. L.. On the inertia group of certain manifolds. J. London Math. Soc. 9 (1974/5), 537–548.Google Scholar
In this list books, surveys and expository papers are marked by stars.Google Scholar