Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-26T21:01:58.880Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary conditions for general ordinary differential operators and their adjoints

Published online by Cambridge University Press:  14 November 2011

W. D. Evans  and
Sobhy E. Ibrahim
W. D. Evans
Affiliation:
School of Mathematics, University of Wales College of Cardiff, Senghenydd Road, Cardiff CF2 4AG, Wales, U.K.
Sobhy E. Ibrahim
Affiliation:
School of Mathematics, University of Wales College of Cardiff, Senghenydd Road, Cardiff CF2 4AG, Wales, U.K.
Get access Rights & Permissions [Opens in a new window]

Synopsis

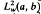A characterisation is obtained of all the regularly solvable operators and their adjoints generated by a general differential expression in . The domains of these operators are described in terms of boundary conditions involving the 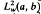solutions of Mu = λwu and the adjoint equation 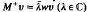. The results include those of Sun Jiong [15] concerning self-adjoint realisations of a symmetric M when the minimal operator has equal deficiency indices: if the deficiency indices are unequal the maximal symmetric operators are determined by the results herein. Another special case concerns the J -self-adjoint operators, where J denotes complex conjugation, and for this we recover the results of Zai-jiu Shang in [16].

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 114 , Issue 1-2 , 1990 , pp. 99 - 117
Copyright
Copyright © Royal Society of Edinburgh 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1Zhi-Jiang, Cao. The self-adjoint domains of second-order differential operators in the limit-circle case. Acta Math. Sinica 28 (1985), 175–180.Google Scholar
2Zhi-jiang, Cao. On self-adjoint extensions in the limit-circle case of differential operators of order n. Ada Math. Sinica 28 (1985), 205–217.Google Scholar
3Edmunds, D. E. and Evans, W. D.. Spectral Theory and Differential Operators (Oxford: Oxford University Press, 1987).Google Scholar
4Evans, W. D.. Regularly solvable extensions of non-self-adjoint ordinary differential operators. Proc. Roy. Soc. Edinburgh Sect. A 97 (1984), 79–95.CrossRefGoogle Scholar
5Everitt, W. N.. A note on the self-ajoint domains of second-order differential equations. Quart. J. Math. Oxford Ser. (2) 14 (1963), 41–45.CrossRefGoogle Scholar
6Everitt, W. N.. Integrable square solutions of ordinary differential equations. Quart. J. Math. Oxford Ser. (2) 14 (1963), 170–180.CrossRefGoogle Scholar
7Everitt, W. N.. Singular differential equations II: some self-adjoint even order cases. Quart. J. Math. Oxford Ser. (2) 18 (1967), 13–32.CrossRefGoogle Scholar
8Everitt, W. N. and Kumar, V. K.. On the Titchmarsh–Weyl theory of ordinary symmetric differential equations I: the general theory. Nieuw Arch. Wisk. (3) 24 (1976), 1–48.Google Scholar
9Everitt, W. N. and Kumar, V. K.. On the Titchmarsh–Weyl theory of ordinary symmetric differential equations II: the odd-order case. Nieuw Arch. Wisk. (3) 24 (1976), 109–145.Google Scholar
10Everitt, W. N. and Race, D.. Some remarks on linear ordinary quasi-differential expressions. Proc. London Math. Soc. (3) 54 (1987), 300–320.CrossRefGoogle Scholar
11Everitt, W. N. and Zettl, A.. Generalized symmetric ordinary differential expressions I: the general theory. Nieuw Arch. Wisk. (3) 27 (1979), 363–397.Google Scholar
12Frentzen, H.. On J-symmetric quasi-differential expressions with matrix-valued coefficients. Quaestiones Math. 10 (1986), 153–164.CrossRefGoogle Scholar
13Hinton, D., Krall, A. M. and Shaw, K.. Boundary conditions for differential operators with intermediate deficiency index. Appl. Anal. 25 (1987), 43–53.CrossRefGoogle Scholar
14Mirsky, L.. An Introduction to Linear Algebra (Oxford: Oxford University Press, 1955).Google Scholar
15Jiong, Sun. On the self-adjoint extensions of symmetric ordinary differential operators with middle deficiency indices. Acta Math. Sinica 2 (1986), 152–167.CrossRefGoogle Scholar
16Shang, Zai-Jiu. On J-selfadjoint extensions of J-symmetric ordinary differential operators. J. Differential Equations 73 (1988), 153–177.CrossRefGoogle Scholar
17Zettl, A.. Formally self-adjoint quasi-differential operators. Rocky Mountain J. Math. 5 (1975), 453–474.CrossRefGoogle Scholar