Article contents
Structure and Stability of Filamentary Clouds Supported by Lateral Magnetic Field
Published online by Cambridge University Press: 12 September 2016
Abstract
We have constructed two types of analytical models for an isothermal filamentary cloud supported mainly by magnetic tension. The first one describes an isolated cloud while the second considers filamentary clouds spaced periodically. The filamentary clouds are assumed to be highly flattened in both the models. The former is proved to be the asymptotic limit of the latter in which each filamentary cloud is much thinner than the distance to the neighboring filaments. These models show that the mass to flux ratio is crucial for the magnetohydrodynamical equilibrium. The upper bound for the line density, i.e., the mass per unit length, is proportional to the magnetic flux. The mass to flux ratio is slightly larger than the critical value, ( 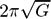 $2 \pi \sqrt{G}$ )−1, in the first model and lower in the second model. The first model is unstable against fragmentation and the wavelength of the fastest growing mode is several times longer than the cloud diameter. The second model is likely to be unstable only when the mass to flux ratio is supercritical.
$2 \pi \sqrt{G}$ )−1, in the first model and lower in the second model. The first model is unstable against fragmentation and the wavelength of the fastest growing mode is several times longer than the cloud diameter. The second model is likely to be unstable only when the mass to flux ratio is supercritical.
Keywords
Information
- Type
- Poster Papers
- Information
- Copyright
- Copyright © International Astronomical Union 2016
References
- 1
- Cited by

