Published online by Cambridge University Press: 21 July 2015
In this paper, we use the Riemann zeta function ζ(x) and the Bessel zeta function ζμ(x) to study the log behaviour of combinatorial sequences. We prove that ζ(x) is log-convex for x > 1. As a consequence, we deduce that the sequence {|B2n|/(2n)!}n ≥ 1 is log-convex, where Bn is the nth Bernoulli number. We introduce the function θ(x) = (2ζ(x)Γ(x + 1)) 1/x, where Γ(x) is the gamma function, and we show that logθ(x) is strictly increasing for x ≥ 6. This confirms a conjecture of Sun stating that the sequence 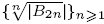 is strictly increasing. Amdeberhan et al. defined the numbers an(μ) = 2 2n+1 (n + 1)!(μ+ 1)nζμ(2n) and conjectured that the sequence {an(μ)}n≥1 is log-convex for μ = 0 and μ = 1. By proving that ζμ(x) is log-convex for x > 1 and μ > -1, we show that the sequence {an(≥)}n>1 is log-convex for any μ > - 1. We introduce another function θμ,(x) involving ζμ(x) and the gamma function Γ(x) and we show that logθμ(x) is strictly increasing for x > 8e(μ + 2)2. This implies that
is strictly increasing. Amdeberhan et al. defined the numbers an(μ) = 2 2n+1 (n + 1)!(μ+ 1)nζμ(2n) and conjectured that the sequence {an(μ)}n≥1 is log-convex for μ = 0 and μ = 1. By proving that ζμ(x) is log-convex for x > 1 and μ > -1, we show that the sequence {an(≥)}n>1 is log-convex for any μ > - 1. We introduce another function θμ,(x) involving ζμ(x) and the gamma function Γ(x) and we show that logθμ(x) is strictly increasing for x > 8e(μ + 2)2. This implies that
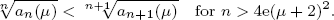
Based on Dobinski’s formula, we prove that
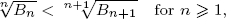
where Bn is the nth Bell number. This confirms another conjecture of Sun. We also establish a connection between the increasing property of 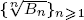 and Holder’s inequality in probability theory.
and Holder’s inequality in probability theory.