Article contents
A Theorem on the Integral of Stieltjes
Published online by Cambridge University Press: 20 January 2009
Extract
In a recent paper Mr J. M. Whittaker has given the following Theorem:—
If ψ (x) be the indefinite Riemann integral of a bounded positive function g(x), and if f(x) be any bounded function, then the equation
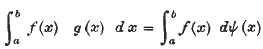
is true whenever either side exists.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1925
References
page 79 note * Proc. Lond. Math. Soc., Ser. II, Vol. 28 (1926), p. 213.
page 79 note † It is only necessary to postulate the existence of ![]() , since that of
, since that of ![]() may then be deduced. [See Pollard: Quarterly Jo., Vol 49 (1923), p. 76 (II)].
may then be deduced. [See Pollard: Quarterly Jo., Vol 49 (1923), p. 76 (II)].
page 80 note * Cf. Carlemann, : Equations Intégrales Singulièrts á Noyau Réel et Symétrique (Uppsala 1923), p. 11.Google Scholar
page 80 note † Ann. Fac. Sc. Toulouse, VIII (1894).Google Scholar
page 80 note ‡ See Hobson, : Functions of a Real Variable (Second Ed.), Vol. I, p. 506Google Scholar, sqq., along with Addendum to p. 508 in Vol. II, p. 774.
page 80 note § Quarterly Jo., Vol. 49 (1923), p. 73.Google Scholar
page 83 note † See footnote † p. 79.
- 4
- Cited by

