No CrossRef data available.
Article contents
A special Pencil of Binary Quartics
Published online by Cambridge University Press: 20 January 2009
Extract
I. If the Jacobian sextic 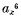 of a pencil of binary quartics is known, the pencil itself is determined in five ways. The explicit determination of the pencil in terms of the irrational invariants of
of a pencil of binary quartics is known, the pencil itself is determined in five ways. The explicit determination of the pencil in terms of the irrational invariants of 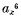 has been effected by Stephanos.
has been effected by Stephanos.
There are two known cases in which a pencil of quartics admits of rational determination from its Jacobian. In these, the rationally determinable pencil differentiates itself algebraically from its remaining four co-Jacobian pencils.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1928
References
page 104 note 1 Mem. I'lnstitut, 27 (1883), 2.Google Scholar
page 104 note 2 The Null Pencil of Binary Quartics, Proc. Lond. Math. Soc., 2, 23 (1923) 317–325.Google Scholar
page 106 note 1 This might be seen most simply by taking the two linearly independent members in the form ![]()
page 108 note 1 Compare Proc. L.M.S. loc. cit.Google Scholar
page 110 note 1 (For the theory of pedo-parallelism of inscribed triangles of a circle, see Proc. Camb. Phil. Soc. 23 (1926), p. 253.Google Scholar

