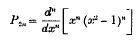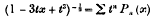Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Milovanović, G. V.
and
Djordjević, G.
1987.
On Some Properties of Humbert’s Polynomials.
The Fibonacci Quarterly,
Vol. 25,
Issue. 4,
p.
356.
Cheikh, Youssèf Ben
2000.
Differential Equations Satisfied by the Components with Respect to the Cyclic Group of Order n of Some Special Functions.
Journal of Mathematical Analysis and Applications,
Vol. 244,
Issue. 2,
p.
483.
Lamiri, I.
and
Ouni, A.
2008.
d-Orthogonality of Humbert and Jacobi type polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 341,
Issue. 1,
p.
24.
Ben Romdhane, N.
2008.
On the zeros of d-symmetric d-orthogonal polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 344,
Issue. 2,
p.
888.
Ben Cheikh, Y.
Lamiri, I.
and
Ouni, A.
2009.
On Askey-scheme and d-orthogonality, I: A characterization theorem.
Journal of Computational and Applied Mathematics,
Vol. 233,
Issue. 3,
p.
621.
Ben Cheikh, Y.
and
Ben Romdhane, N.
2011.
Ond-symmetric classicald-orthogonal polynomials.
Journal of Computational and Applied Mathematics,
Vol. 236,
Issue. 1,
p.
85.
Romdhane, Neila Ben
and
Gaied, Mohamed
2016.
A generalization of the symmetric classical polynomials: Hermite and Gegenbauer polynomials.
Integral Transforms and Special Functions,
Vol. 27,
Issue. 3,
p.
227.
Dobashi, Nobuyuki
Suzuki, Erika
Watanabe, Shigeru
and
Liu, Lishan
2017.
Some polynomials defined by generating functions and differential equations.
Cogent Mathematics,
Vol. 4,
Issue. 1,
p.
1278830.
Srivastava, H.M.
Kucukoğlu, Irem
and
Simsek, Yilmaz
2017.
Partial differential equations for a new family of numbers and polynomials unifying the Apostol-type numbers and the Apostol-type polynomials.
Journal of Number Theory,
Vol. 181,
Issue. ,
p.
117.
Wang, Weiping
and
Wang, Hui
2017.
Generalized Humbert polynomials via generalized Fibonacci polynomials.
Applied Mathematics and Computation,
Vol. 307,
Issue. ,
p.
204.
Li, Yingbo
and
Clyde, Merlise A.
2018.
Mixtures ofg-Priors in Generalized Linear Models.
Journal of the American Statistical Association,
Vol. 113,
Issue. 524,
p.
1828.
Mesk, Mohammed
and
Zahaf, Mohammed Brahim
2018.
On a class ofd-symmetric polynomial sets generated byF(xt—R(t)).
Integral Transforms and Special Functions,
Vol. 29,
Issue. 12,
p.
979.
Srivastava, H. M.
Khan, Waseem A.
and
Haroon, Hiba
2019.
Some expansions for a class of generalized Humbert matrix polynomials.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 113,
Issue. 4,
p.
3619.
Wang, Weiping
and
Zhang, Chenlu
2019.
Riordan arrays and related polynomial sequences.
Linear Algebra and its Applications,
Vol. 580,
Issue. ,
p.
262.
Loureiro, Ana F.
and
Van Assche, Walter
2020.
Three-fold symmetric Hahn-classical multiple orthogonal polynomials.
Analysis and Applications,
Vol. 18,
Issue. 02,
p.
271.
Lamiri, Imed
and
Weslati, Jihen
2021.
Asymptotic relations involving 𝑑-orthogonal polynomials.
Georgian Mathematical Journal,
Vol. 28,
Issue. 3,
p.
383.
Dattoli, G.
Germano, B.
Licciardi, S.
and
Martinelli, M. R.
2021.
Integrals of Special Functions and Umbral Methods.
International Journal of Applied and Computational Mathematics,
Vol. 7,
Issue. 4,
Fouskakis, Dimitris
and
Ntzoufras, Ioannis
2022.
Power-Expected-Posterior Priors as Mixtures of g-Priors in Normal Linear Models.
Bayesian Analysis,
Vol. 17,
Issue. 4,
Bhootna, Niharika
Dhull, Monika Singh
Kumar, Arun
and
Leonenko, Nikolai
2023.
Humbert generalized fractional differenced ARMA processes.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 125,
Issue. ,
p.
107412.
Savalia, Rajesh V.
2023.
THE GENERAL INVERSION PAIR AND ITS APPLICATIONS.
Rocky Mountain Journal of Mathematics,
Vol. 53,
Issue. 4,