Hostname: page-component-7dd5485656-pnlb5 Total loading time: 0.001 Render date: 2025-10-31T04:03:10.778Z Has data issue: false hasContentIssue false
  • English
  • Français

Series expansion, higher-order monotonicity properties and inequalities for the modulus of the Grötzsch ring

Part of: Real functions Other special functions Geometric function theory

Published online by Cambridge University Press:  15 November 2024

Zhen-Hang Yang Open the ORCID record for Zhen-Hang Yang [Opens in a new window] ,
Miao-Kun Wang Open the ORCID record for Miao-Kun Wang [Opens in a new window]  and
Jing-Feng Tian Open the ORCID record for Jing-Feng Tian [Opens in a new window]
Zhen-Hang Yang
Affiliation:
Zhejiang Electric Power Company Research Institute, Hangzhou, Zhejiang, P. R. China
Miao-Kun Wang*
Affiliation:
Department of Mathematics, Huzhou University, Huzhou, Zhejiang, P. R. China
Jing-Feng Tian
Affiliation:
Department of Mathematics and Physics, North China Electric Power University, Baoding, Hebei, P.R. China
*
Corresponding author: Miao-Kun Wang, email: wmk000@126.com
Get access Rights & Permissions [Opens in a new window]

Abstract

For 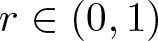$r\in(0,1)$, let $\mu \left( r\right) $ be the modulus of the plane Grötzsch ring 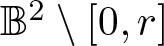$\mathbb{B}^2\setminus[0,r]$, where 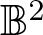$\mathbb{B}^2$ is the unit disk. In this paper, we prove that

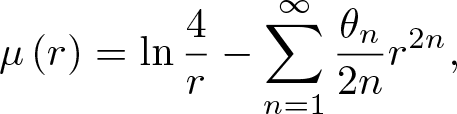\begin{equation*}\mu \left( r\right) =\ln \frac{4}{r}-\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}r^{2n},\end{equation*}

with 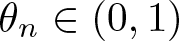$\theta _{n}\in \left( 0,1\right)$. Employing this series expansion, we obtain several absolutely monotonic and (logarithmically) completely monotonic functions involving 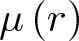$\mu \left( r\right) $, which yields some new results and extend certain known ones. Moreover, we give an affirmative answer to the conjecture proposed by Alzer and Richards in H. Alzer and K. Richards, On the modulus of the Grötzsch ring, J. Math. Anal. Appl. 432(1): (2015), 134–141, DOI 10.1016/j.jmaa.2015.06.057. As applications, several new sharp bounds and functional inequalities for 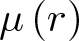$\mu \left( r\right) $ are established.

Keywords

complete elliptic integralmodulus of the Grötzsch ringabsolute monotonicityseries expansioncomplete monotonicityinequality

MSC classification

Primary: 33E05: Elliptic functions and integrals 30C62: Quasiconformal mappings in the plane
Secondary: 26A48: Monotonic functions, generalizations 39B62: Functional inequalities, including subadditivity, convexity, etc.

Information

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 68 , Issue 1 , February 2025 , pp. 16 - 43
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alzer, H. and Richards, K., On the modulus of the Grötzsch ring, J. Math. Anal. Appl. 432(1) (2015), 134–141. doi:10.1016/j.jmaa.2015.06.057CrossRefGoogle Scholar
Anderson, G. D., Qiu, S.-L., Vamanamurthy, M. K. and Vuorinen, M., Generalized elliptic integrals and modular equations, Pacific J. Math. 192(1) (2000), 1–37. doi:10.2140/pjm.2000.192.1CrossRefGoogle Scholar
Anderson, G. D., Qiu, S.-L. and Vuorinen, M., Modular equations and distortion functions, Ramanujan J. 18(2) (2009), 147–169. doi:10.1007/s11139-007-9047-3CrossRefGoogle Scholar
Anderson, G. D., Vamanamurthy, M. K. and Vuorinen, M., Functional inequalities for complete elliptic integrals and their ratios, SIAM J. Math. Anal. 21(2) (1990), 536–549. doi:10.1137/0521029CrossRefGoogle Scholar
Anderson, G. D., Vamanamurthy, M. K. and Vuorinen, M., Topics in special functions II, Conform. Geom. Dyn. 11(17) (2007), 250–270. doi:10.1090/S1088-4173-07-00168-3CrossRefGoogle Scholar
Anderson, G. D., Vamanamurthy, M. K. and Vuorinen, M. K., Conformal invariants, inequalities, and quasiconformal maps, (John Wiley & Sons, New York, NY, 1997).Google Scholar
Atanassov, R. D. and Tsoukrovski, U. V., Some properties of a class of logarithmically completely monotonic functions, C. R. Acad. Bulg. Sci. 41(2) (1988), 21–23.Google Scholar
Balasubramaniana, R., Ponnusamy, S. and Vuorinen, M., Functional inequalities for the quotients of hypergeometric functions, J. Math. Anal. Appl. 218(1) (1998), 256–268. doi:10.1006/jmaa.1997.5776CrossRefGoogle Scholar
Barnard, R. W., Pearce, K. and Richards, K. C., A monotonicity property involving $_{3}F_{2}$ and comparisons of the classical approximations of elliptical arc length, SIAM J. Math. Anal. 32(2) (2000), 403–419. doi:10.1137/S003614109935050XCrossRefGoogle Scholar
Berg, C., Integral representation of some functions related to the gamma function, Mediterr. J. Math. 1(4) (2004), 433–439. doi:10.1007/s00009-004-0022-6CrossRefGoogle Scholar
Bernstein, S. N., Sur les fonctions absolument monotones, Acta Math. 52(1) (1928), 1–66. doi:10.1007/BF02592679CrossRefGoogle Scholar
Biernacki, M. and Krzyz, J., On the monotonicity of certain functionals in the theory of analytic functions, Annales Universitatis Mariae Curie-Sklodowska 9(1) (1955), 135–147.Google Scholar
Borwein, J. M. and Borwein, P. B., Pi and AGM, (John Wiley & Sons, New York, NY, 1987).Google Scholar
Byrd, P. F. and Friedman, M. D., Handbook of elliptic integrals for engineers and scientists, (Springer-Verlag, New York, NY, 1971).CrossRefGoogle Scholar
Chen, C.-P., Qi, F. and Srivastava, H. M., Some properties of functions related to the gamma and psi functions, Integral Transforms Spec. Funct. 21(2) (2010), 153–164. doi:10.1080/10652460903064216CrossRefGoogle Scholar
Lehto, O. and Virtanen, K.I., Quasiconformal mappings in the plane (2nd ed.), Die Grundlehren der Mathematischen Wissenschaften, (Spring-Verlag, New York, NY-Heidelberg, 1973).CrossRefGoogle Scholar
Miller, K. S. and Samko, S. G., Completely monotonic functions, Integral Transforms Spec. Funct. 12(4) (2001), 389–402. doi:10.1080/10652460108819360CrossRefGoogle Scholar
Qi, F. and Chen, C. P., A complete monotonicity property of the gamma function, J. Math. Anal. Appl. 296(2) (2004), 603–607. doi:10.1016/j.jmaa.2004.04.026CrossRefGoogle Scholar
Qiu, S.-L. and Vuorinen, M., Duplication inequalities for the ratios of hypergeometric functions, Forum Math. 12(1) (2000), 109–133. doi:10.1515/form.1999.025Google Scholar
Qiu, S. L. and Vuorinen, M., Infinite products and the normalized quotients of hypergeometric functions, SIAM J. Math. Anal. 30(5) (1999), 1057–1075. doi:10.1137/S0036141097326805CrossRefGoogle Scholar
Richards, K. C., A note on inequalities for the ratio of zero-balanced hypergeometric functions, Proc. Amer, Math. Soc. Ser. B 6(2) (2019), 15–20. doi:10.1090/bproc/41CrossRefGoogle Scholar
Schilling, R. L., Song, R. and Vondra\u cek, Z., Bernstein functions: theory and applications, (De Gruyter, Berlin, 2010).Google Scholar
Tian, J.-F., Ha, M.-H. and Xing, H.-J., Properties of the power-mean and their applications, AIMS Math. 5(6) (2020), 7285–7300. doi:10.3934/math.2020466CrossRefGoogle Scholar
Tian, J.-F. and Yang, Z.-H., Several absolutely monotonic functions related to the complete elliptic integral, Results Math. 77(3, paper no. 109) (2022), . doi:10.1007/s00025-022-01641-4CrossRefGoogle Scholar
Tian, J.-F. and Yang, Z.-H., Convexity and monotonicity involving the complete elliptic integral of the first kind, Results Math. 78(1, paper no. 29) (2023), . doi:10.1007/s00025-022-01799-xCrossRefGoogle Scholar
Wang, G.-D., Qiu, S.-L., Zhang, X. H. and Chu, Y.-M., Approximate convexity and concavity of generalized Grözsch ring function, Appl. Math.- J. Chin. Univ. 21(2) (2006), 203–206. doi:10.1007/BF02791357Google Scholar
Wang, G.-D., Zhang, X.-H., Qiu, S.-L. and Chu, Y.-M., The bounds of the solutions to generalized modular equations, J. Math. Anal. Appl. 321(2) (2006), 589–594. doi:10.1016/j.jmaa.2005.08.064CrossRefGoogle Scholar
Wang, M.-K., Chu, H.-H. and Chu, Y.-M., On the approximation of some special functions in Ramanujan’s generalized modular equation with signature 3, Ramanujan J. 56(1) (2021), 1–22. doi:10.1007/s11139-021-00437-4CrossRefGoogle Scholar
Wang, M.-K., Chu, H.-H., Li, Y.-M. and Chu, Y.-M., Answers to three conjectures on convexity of three functions involving complete elliptic integrals of the first kind, Appl. Anal. Discrete Math. 14(1) (2020), 255–271. doi:10.2298/AADM190924020WCrossRefGoogle Scholar
Wang, M.-K., Li, Y.-M. and Chu, Y.-M., Inequalities and infinite product formula for Ramanujan generalized modular equation function, Ramanujan J. 46(1) (2018), 189–200. doi:10.1007/s11139-017-9888-3CrossRefGoogle Scholar
Widder, D. V., The Laplace transform, (Princeton University Press, Princeton, 1946).Google Scholar
Yang, Z.-H., Chu, Y.-M. and Wang, M.-K., Monotonicity criterion for the quotient of power series with applications, J. Math. Anal. Appl. 428(1) (2015), 587–604. doi:10.1016/j.jmaa.2015.03.043CrossRefGoogle Scholar
Yang, Z.-H. and Tian, J.-F., Absolutely monotonic functions involving the complete elliptic integrals of the first kind with applications, J. Math. Inequal. 15(3) (2021), 1299–1310. doi:10.7153/jmi-2021-15-87CrossRefGoogle Scholar
Yang, Z.-H. and Tian, J.-F., Absolute monotonicity involving the complete elliptic integrals of the first kind with applications, Acta Math. Sci. Ser. B, Engl. Ed. 42(3) (2022), 847–864. doi:10.1007/s10473-022-0302-xCrossRefGoogle Scholar
Yang, Z.-H.. A new way to prove L’Hospital monotone rules with applications, arXiv:1409.6408, 2014, .Google Scholar
Yang, Z.-H., Sharp approximations for the complete elliptic integrals of the second kind by one-parameter means, J. Math. Anal. Appl. 467(1) (2018), 446–461. doi:10.1016/j.jmaa.2018.07.020CrossRefGoogle Scholar
Zhang, X.-H., Wang, G.-D. and Chu, Y.-M., Some inequalities for the generalized Grötzsch function, Proc. Edinb. Math. Soc. (2) 51(1) (2008), 265–272. doi:10.1017/S001309150500132XCrossRefGoogle Scholar
Zhang, X.-H., On the generalized modulus, Ramanujan J. 43(2) (2017), 405–413. doi:10.1007/s11139-015-9746-0CrossRefGoogle Scholar