Hostname: page-component-7dd5485656-dk7s8 Total loading time: 0 Render date: 2025-10-30T22:32:26.777Z Has data issue: false hasContentIssue false
  • English
  • Français

Products of idempotents in certain semigroups of transformations

Published online by Cambridge University Press:  20 January 2009

J. M. Howie
J. M. Howie
Affiliation:
University of St. Andrews
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

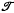In an earlier paper (5) a description was given in set-theoretic terms of the semigroup generated by the idempotents of a full transformation semigroup , one of the results being that if X is finite then every element of 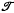that is not bijective is expressible as a product of idempotents. In view of this it was natural to ask whether by analogy every singular square matrix is expressibleas a product of idempotent matrices. This is indeed the case, as was shown by J. A. Erdos (2). Magill (6) has considered products of idempotents in thesemigroup of all continuous self-maps of a topological space X, but a comparable characterization of products of idempotents in this case appears to be extremelydifficult, and no solution is available yet.

Information

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 17 , Issue 3 , June 1971 , pp. 223 - 236
Copyright
Copyright © Edinburgh Mathematical Society 1971

References

REFERENCES

(1)Durell, Clement V.. and Robson, A., Advanced Algebra, vol. II (London, 1937).Google Scholar
(2)Erdos, J. A., On products of idempotent matrices, Glasgow Math. J. 8 (1967), 118–122.CrossRefGoogle Scholar
(3)Harris, Bernard, A note on the number of idempotent elements in symmetric semigroups, Amer. Math. Monthly 74 (1967), 1234–1235.CrossRefGoogle Scholar
(4)Harris, Bernard and Schoenfeld, Lowell, The number of idempotent elements in symmetric semigroups, J. Combinatorial Theory 3 (1967), 122–135.CrossRefGoogle Scholar
(5)Howie, J. M., The subsemigroup generated by the idempotents of a full transformation semigroup, J. London Math. Soc. 41 (1966), 707–716.CrossRefGoogle Scholar
(6)Magill, K. D. Jr., Semigroups of functions generated by idempotents, J. London Math. Soc. 44 (1969), 236–242.CrossRefGoogle Scholar
(7)Mullin, R. C. and Stanton, R. G., A combinatorial property of spanning forests in connected graphs, J. Combinatorial Theory 3 (1967), 236–243.CrossRefGoogle Scholar
(8)Tainiter, M., A characterization of idempotents in semigroups, J. Combinatorial Theory 5 (1968), 370–373.CrossRefGoogle Scholar