Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Coxeter, H. S. M.
1937.
Abstract definitions for the symmetry groups of the regular polytopes, in terms of two generators. Part II: the rotation groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 33,
Issue. 3,
p.
315.
Coxeter, H. S. M.
1939.
The abstract groups 𝐺^{𝑚,𝑛,𝑝}.
Transactions of the American Mathematical Society,
Vol. 45,
Issue. 1,
p.
73.
Shephard, G. C.
1953.
Unitary Groups Generated by Reflections.
Canadian Journal of Mathematics,
Vol. 5,
Issue. ,
p.
364.
Shephard, G. C.
and
Todd, J. A.
1954.
Finite Unitary Reflection Groups.
Canadian Journal of Mathematics,
Vol. 6,
Issue. ,
p.
274.
Coxetek, H. S. M.
1956.
The collineation groups of the finite affine and projective planes with four lines through each point.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 20,
Issue. 3-4,
p.
165.
Leech, John
1962.
Some definitions of Klein's simple group of order 168 and other groups.
Proceedings of the Glasgow Mathematical Association,
Vol. 5,
Issue. 4,
p.
166.
Leech, John
1963.
Coset enumeration on digital computers.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 59,
Issue. 2,
p.
257.
Trotter, H. F.
1964.
A Machine Program for Coset Enumeration.
Canadian Mathematical Bulletin,
Vol. 7,
Issue. 3,
p.
357.
Mendelsohn, N. S.
1964.
An Algorithmic Solution for a Word Problem in Group Theory.
Canadian Journal of Mathematics,
Vol. 16,
Issue. ,
p.
509.
Leech, John
1965.
Generators for certain normal subgroups of (2,3,7).
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 61,
Issue. 2,
p.
321.
Neumann, B. H.
1967.
Some Remarks on Semigroup Presentations.
Canadian Journal of Mathematics,
Vol. 19,
Issue. ,
p.
1018.
NEUBÜSER, J.
1970.
Computational Problems in Abstract Algebra.
p.
1.
LEECH, JOHN
1970.
Computational Problems in Abstract Algebra.
p.
21.
Fleischer, Klaus-J�rgen
1972.
Eine Kennzeichnung der symplektischen und orthogonalen Gruppen �berGF(4).
Mathematische Zeitschrift,
Vol. 124,
Issue. 2,
p.
100.
Cannon, John J.
Dimino, Lucien A.
Havas, George
and
Watson, Jane M.
1973.
Implementation and analysis of the Todd-Coxeter algorithm.
Mathematics of Computation,
Vol. 27,
Issue. 123,
p.
463.
Dietze, Anke
and
Schaps, Mary
1974.
Determining Subgroups of a Given Finite Index in a Finitely Presented Group.
Canadian Journal of Mathematics,
Vol. 26,
Issue. 4,
p.
769.
Beetham, M. J.
and
Campbell, C. M.
1976.
A note on the Todd-Coxeter coset enumeration algorithm.
Proceedings of the Edinburgh Mathematical Society,
Vol. 20,
Issue. 1,
p.
73.
McLain, D. H.
1977.
An algorithm for determining defining relations of a subgroup.
Glasgow Mathematical Journal,
Vol. 18,
Issue. 1,
p.
51.
Jura, Andrzej
1978.
Coset Enumeration in a Finitely Presented Semigroup.
Canadian Mathematical Bulletin,
Vol. 21,
Issue. 1,
p.
37.
Neumann, B. H.
1979.
Proofs.
The Mathematical Intelligencer,
Vol. 2,
Issue. 1,
p.
18.
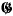 , that is, a set of relations
, that is, a set of relations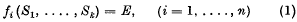
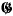 , such that every other relation between S1, …., Sk is an algebraic consequence of (1).
, such that every other relation between S1, …., Sk is an algebraic consequence of (1).
