No CrossRef data available.
Published online by Cambridge University Press: 18 October 2023
This work characterizes the vanishing of the Fourier coefficients of all CM (Complex Multiplication) eta quotients. As consequences, we recover Serre’s characterization about that of 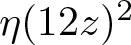 $\eta(12z)^{2}$ and recent results of Chang on the pth coefficients of
$\eta(12z)^{2}$ and recent results of Chang on the pth coefficients of 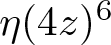 $\eta(4z)^{6}$ and
$\eta(4z)^{6}$ and 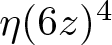 $\eta(6z)^{4}$. Moreover, we generalize the results on the cases of weight 1 to the setting of binary quadratic forms.
$\eta(6z)^{4}$. Moreover, we generalize the results on the cases of weight 1 to the setting of binary quadratic forms.