No CrossRef data available.
Article contents
On the characters of affine Kac–Moody groups
Published online by Cambridge University Press: 20 January 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let G be an affine Kac–Moody group over ℂ, and V∞ an integrable simple quotient of a Verma module for g. Let Gmin be the subgroup of G generated by the maximal algebraic torus T, and the real root subgroups.
It is shown that 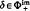 (the least positive imaginary root) gives a character δ∈Hom(G, ℂ*) such that the pointwise character χ∞ of V∞ may be defined on Gmin ∩ G>1.
(the least positive imaginary root) gives a character δ∈Hom(G, ℂ*) such that the pointwise character χ∞ of V∞ may be defined on Gmin ∩ G>1.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1993
References
REFERENCES
1.Carter, R. W., Finite Groups of Lie Type: Conjugacy Classes and Complex Characters (J. Wiley, 1985).Google Scholar
2.Feingold, A. J. and Lepowsky, J., The Weyl-Kac character formula and power series identities, Adv. Math. 29 (1978), 271–309.CrossRefGoogle Scholar
3.Garland, H., The arithmetic theory of loop algebras, Publ. Math. I.H.E.S. 52 (1980), 5–36.CrossRefGoogle Scholar
5.Kac, V. G., Constructing groups associated to infinite dimensional Lie algebras, in Infinite Dimensional Groups with Applications (ed. Kac, V. G., MSRI Publ. 4, Springer-Verlag, 1985).CrossRefGoogle Scholar
6.Kac, V. G. and Peterson, D. H., Unitary structure in representations of infinite dimensional groups and a convexity theorem, Invent. Math. 76 (1984), 1–14.CrossRefGoogle Scholar
7.Looijenga, E., Invariant theory for generalized root systems, Invent, Math. 61 (1980), 1–32.CrossRefGoogle Scholar
9.Slodowy, P., An adjoint quotient for certain groups attached to Kac–Moody algebras Infinite Dimensional Groups with Applications (ed. Kac, V. G., MSRI Publ. 4, Springer-Verlag, 1985).CrossRefGoogle Scholar
10.Slodowy, P., A character approach to Looijenga's invariant theory for generalized root systems, Compositio Math. 55 (1985), 3–32.Google Scholar
11.Slodowy, P., On the Geometry of Schubert Varieties Attached to Kac-Moody Lie Algebras, (Canadian Math. Soc. Proceedings 6, 1986).Google Scholar
12.Tits, J., Uniqueness and presentation of Kac-Moody groups over fields, J. Algebra 105 (1987), 542–573.CrossRefGoogle Scholar
14.Weidmann, J., Linear Operators in Hilbert Spaces (GTM, Springer-Verlag, 1980).CrossRefGoogle Scholar

