Article contents
On Spheroidal Harmonics and Allied Functions
Published online by Cambridge University Press: 20 January 2009
Extract
In a paper recently read before this Society, Mr E. Blades obtained a general formula for spheroidal harmonics in the form of the general solution of Laplace's equation given by Professor Whittaker,
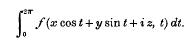
If spheroidal coordinates r, θ, φ are defined by
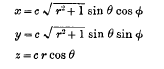
the result obtained is
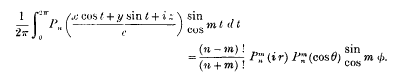
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1914
References
* Proc. Edin. Math. Soc., Vol. XXXIII. (Part I.), 1915, p. 65.Google Scholar
† Kugelfunctionen 1, p. 333.Google Scholar
* e.g. That employed in Whittaker's Modern Analysis.
* Gray and Mathew's Bessel's Functions, p. 27 and p. 92Google Scholar. We have followed the notation there used for the second solution of Bessel's equation, but it is clear that in this case Y m may be taken as any linear combination of the two solutions in which the coefficients are independent of m.
- 2
- Cited by

