Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Varea, V. R.
1999.
Lower semimodular Lie algebras.
Proceedings of the Edinburgh Mathematical Society,
Vol. 42,
Issue. 3,
p.
521.

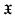 the class of Lie algebras all of whose maximal subalgebras have codimension 1 in
the class of Lie algebras all of whose maximal subalgebras have codimension 1 in 