Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Berman, Robert J.
2021.
Convergence Rates for Discretized Monge–Ampère Equations and Quantitative Stability of Optimal Transport.
Foundations of Computational Mathematics,
Vol. 21,
Issue. 4,
p.
1099.
Mérigot, Quentin
and
Thibert, Boris
2021.
Geometric Partial Differential Equations - Part II.
Vol. 22,
Issue. ,
p.
133.
Hütter, Jan-Christian
and
Rigollet, Philippe
2021.
Minimax estimation of smooth optimal transport maps.
The Annals of Statistics,
Vol. 49,
Issue. 2,
Li, Wenbo
and
Nochetto, Ricardo H
2021.
Quantitative stability and error estimates for optimal transport plans.
IMA Journal of Numerical Analysis,
Vol. 41,
Issue. 3,
p.
1941.
Bansil, Mohit
and
Kitagawa, Jun
2022.
Quantitative Stability in the Geometry of Semi-discrete Optimal Transport.
International Mathematics Research Notices,
Vol. 2022,
Issue. 10,
p.
7354.
Cai, Tianji
Cheng, Junyi
Schmitzer, Bernhard
and
Thorpe, Matthew
2022.
The Linearized Hellinger--Kantorovich Distance.
SIAM Journal on Imaging Sciences,
Vol. 15,
Issue. 1,
p.
45.
Ghosal, Promit
and
Sen, Bodhisattva
2022.
Multivariate ranks and quantiles using optimal transport: Consistency, rates and nonparametric testing.
The Annals of Statistics,
Vol. 50,
Issue. 2,
Carlier, Guillaume
Pegon, Paul
and
Tamanini, Luca
2023.
Convergence rate of general entropic optimal transport costs.
Calculus of Variations and Partial Differential Equations,
Vol. 62,
Issue. 4,
Delalande, Alex
and
Mérigot, Quentin
2023.
Quantitative stability of optimal transport maps under variations of the target measure.
Duke Mathematical Journal,
Vol. 172,
Issue. 17,
Carlier, Guillaume
2023.
Fenchel–Young Inequality with a Remainder and Applications to Convex Duality and Optimal Transport.
SIAM Journal on Optimization,
Vol. 33,
Issue. 3,
p.
1463.
Khurana, Varun
Kannan, Harish
Cloninger, Alexander
and
Moosmüller, Caroline
2023.
Supervised learning of sheared distributions using linearized optimal transport.
Sampling Theory, Signal Processing, and Data Analysis,
Vol. 21,
Issue. 1,
Moosmüller, Caroline
and
Cloninger, Alexander
2023.
Linear optimal transport embedding: provable Wasserstein classification for certain rigid transformations and perturbations.
Information and Inference: A Journal of the IMA,
Vol. 12,
Issue. 1,
p.
363.
Manole, Tudor
Balakrishnan, Sivaraman
Niles-Weed, Jonathan
and
Wasserman, Larry
2024.
Plugin estimation of smooth optimal transport maps.
The Annals of Statistics,
Vol. 52,
Issue. 3,
Sarrazin, Clément
and
Schmitzer, Bernhard
2024.
Linearized Optimal Transport on Manifolds.
SIAM Journal on Mathematical Analysis,
Vol. 56,
Issue. 4,
p.
4970.
Crook, Oliver M.
Cucuringu, Mihai
Hurst, Tim
Schönlieb, Carola-Bibiane
Thorpe, Matthew
and
Zygalakis, Konstantinos C.
2024.
A linear transportation Lp distance for pattern recognition.
Pattern Recognition,
Vol. 147,
Issue. ,
p.
110080.
Carlier, Guillaume
Chizat, Lénaïc
and
Laborde, Maxime
2024.
Displacement smoothness of entropic optimal transport.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 30,
Issue. ,
p.
25.
Deligiannidis, George
de Bortoli, Valentin
and
Doucet, Arnaud
2024.
Quantitative uniform stability of the iterative proportional fitting procedure.
The Annals of Applied Probability,
Vol. 34,
Issue. 1A,
Blickhan, Tobias
2024.
A Registration Method for Reduced Basis Problems Using Linear Optimal Transport.
SIAM Journal on Scientific Computing,
Vol. 46,
Issue. 5,
p.
A3177.
Divol, Vincent
Niles-Weed, Jonathan
and
Pooladian, Aram-Alexandre
2025.
Tight Stability Bounds for Entropic Brenier Maps.
International Mathematics Research Notices,
Vol. 2025,
Issue. 7,
Cloninger, Alexander
Hamm, Keaton
Khurana, Varun
and
Moosmüller, Caroline
2025.
Linearized Wasserstein dimensionality reduction with approximation guarantees.
Applied and Computational Harmonic Analysis,
Vol. 74,
Issue. ,
p.
101718.

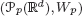 ). We prove that in most cases such a map is no more than 1/
). We prove that in most cases such a map is no more than 1/