No CrossRef data available.
Article contents
Note on Whittaker's Solution of Laplace's Equation
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
§1. Whittaker has shewn that a general solution of Laplace's Equation
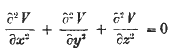
may be put in the form
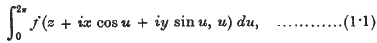
where f (v, u) denotes an arbitrary function of the two variables u and v; such a representation is valid only in the neighbourhood of a regular point.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1925
References
page 22 note * Math. Ann. 57, (1902), 333.Google Scholar
page 23 note * See Whittaker, and Watson, : Modern Analysis (3rd Edn). 329.Google Scholar We are using Hobson's definition (Phil. Trans. A 187 (1896))Google Scholar of the associated functions.
page 24 note * Loc. cit., 499.
page 24 note † Watson, G. N.: Camb. Phil. Trans., 22, (1918), 277–308.Google Scholar

