1. Introduction
Polyhedral products are topological spaces formed by attaching products of spaces together according to an underlying simplicial complex. The study of polyhedral products is of interest across many different disciplines of mathematics, including toric topology, combinatorics, geometric group theory and complex geometry [Reference Bahri, Bendersky and Cohen5]. Specifically, let ![]() $K$ be a simplicial complex on
$K$ be a simplicial complex on ![]() $m$ vertices. For
$m$ vertices. For ![]() $1 \leq i \leq m$, let
$1 \leq i \leq m$, let ![]() $(X_i,A_i)$ be a pair of pointed
$(X_i,A_i)$ be a pair of pointed ![]() $CW$-complexes, where
$CW$-complexes, where ![]() $A_i$ is a pointed
$A_i$ is a pointed ![]() $CW$ subcomplex of
$CW$ subcomplex of ![]() $X_i$. Let
$X_i$. Let ![]() $(\underline{X}, \underline{A})= \{(X_i,A_i)\}^{m}_{i=1}$ be the sequence of
$(\underline{X}, \underline{A})= \{(X_i,A_i)\}^{m}_{i=1}$ be the sequence of ![]() $CW$-pairs. We can identify each simplex
$CW$-pairs. We can identify each simplex ![]() $\sigma \in K$ with the sequence
$\sigma \in K$ with the sequence ![]() $(i_1,\dots,i_k)$ where
$(i_1,\dots,i_k)$ where ![]() $i_1,\dots,i_k$ are the vertices of
$i_1,\dots,i_k$ are the vertices of ![]() $\sigma$ and
$\sigma$ and ![]() $i_1 \lt \dots \lt i_k$. Define
$i_1 \lt \dots \lt i_k$. Define ![]() $(\underline{X},\underline{A})^{\sigma}$ as
$(\underline{X},\underline{A})^{\sigma}$ as
 \begin{equation*}(\underline{X},\underline{A})^{\sigma} = \prod^{m}_{i=1} Y_i, \;\; Y_i = \begin{cases} X_i & i \in \sigma \\ A_i & \mathrm{otherwise}. \end{cases} \end{equation*}
\begin{equation*}(\underline{X},\underline{A})^{\sigma} = \prod^{m}_{i=1} Y_i, \;\; Y_i = \begin{cases} X_i & i \in \sigma \\ A_i & \mathrm{otherwise}. \end{cases} \end{equation*}The polyhedral product associated to K is defined as
 \begin{equation*}(\underline{X},\underline{A})^{K} =\bigcup_{\sigma \in K} (\underline{X},\underline{A})^{\sigma} \subseteq \prod^{m}_{i=1} X_i.\end{equation*}
\begin{equation*}(\underline{X},\underline{A})^{K} =\bigcup_{\sigma \in K} (\underline{X},\underline{A})^{\sigma} \subseteq \prod^{m}_{i=1} X_i.\end{equation*} An important special case is the moment-angle complex, denoted ![]() ${\mathcal{Z}}_K$, which is the polyhedral product where each pair is
${\mathcal{Z}}_K$, which is the polyhedral product where each pair is ![]() $(D^2,S^1)$. There are two problems that provide motivation for this work: how the homotopy type of the polyhedral product changes under simplicial operations, and determining the homotopy type of loop spaces of polyhedral products.
$(D^2,S^1)$. There are two problems that provide motivation for this work: how the homotopy type of the polyhedral product changes under simplicial operations, and determining the homotopy type of loop spaces of polyhedral products.
It is well known that the polyhedral product on the join of two simplicial complexes is the Cartesian product of polyhedral products on each complex, and in [Reference Theriault26], a homotopy equivalence for the loop space of the polyhedral product on the connected sum of simplicial complexes was given. In this paper, we consider how the homotopy theory of the moment-angle complex changes under the polyhedral join product operation, which is defined similarly to the polyhedral product operation, but with pairs of spaces ![]() $(X_i,A_i)$ and the Cartesian product being replaced with pairs of simplicial complexes
$(X_i,A_i)$ and the Cartesian product being replaced with pairs of simplicial complexes ![]() $(K_i,L_i)$ and the join operation. To be exact, let
$(K_i,L_i)$ and the join operation. To be exact, let ![]() $M$ be a simplicial complex on
$M$ be a simplicial complex on ![]() $[m]$. For
$[m]$. For ![]() $1\leq i \leq m$, and let
$1\leq i \leq m$, and let ![]() $(\underline{K}, \underline{L})= \{(K_i,L_i)\}^{m}_{i=1}$ be a sequence of pairs of simplicial complexes, where
$(\underline{K}, \underline{L})= \{(K_i,L_i)\}^{m}_{i=1}$ be a sequence of pairs of simplicial complexes, where ![]() $L_i$ is a subcomplex on
$L_i$ is a subcomplex on ![]() $K_i$, considered to be on the vertex set of
$K_i$, considered to be on the vertex set of ![]() $K_i$. We can identify each simplex
$K_i$. We can identify each simplex ![]() $\sigma \in M$ with the sequence
$\sigma \in M$ with the sequence ![]() $(i_1,...,i_k)$ where
$(i_1,...,i_k)$ where ![]() $i_1,...,i_k$ are the vertices of
$i_1,...,i_k$ are the vertices of ![]() $\sigma$ and
$\sigma$ and ![]() $i_1 \lt \dots \lt i_k$. Define
$i_1 \lt \dots \lt i_k$. Define ![]() $(\underline{K},\underline{L})^{*\sigma}$ as the following subcomplex of
$(\underline{K},\underline{L})^{*\sigma}$ as the following subcomplex of ![]() $K_1*\dots*K_m$:
$K_1*\dots*K_m$:
 \begin{equation*}
(\underline{K},\underline{L})^{*\sigma} = \overset{m}{\underset{i=1} \ast} \; Y_i,\;\; Y_i = \begin{cases} K_i & i \in \sigma \\ L_i & \mathrm{otherwise}. \end{cases}
\end{equation*}
\begin{equation*}
(\underline{K},\underline{L})^{*\sigma} = \overset{m}{\underset{i=1} \ast} \; Y_i,\;\; Y_i = \begin{cases} K_i & i \in \sigma \\ L_i & \mathrm{otherwise}. \end{cases}
\end{equation*}The polyhedral join product is defined as
 \begin{equation*}(\underline{K},\underline{L})^{*M} = \bigcup_{\sigma \in M} (\underline{K},\underline{L})^{*\sigma}.\end{equation*}
\begin{equation*}(\underline{K},\underline{L})^{*M} = \bigcup_{\sigma \in M} (\underline{K},\underline{L})^{*\sigma}.\end{equation*}The polyhedral join product produces a new simplicial complex, but retains the combinatorial qualities of the ingredient complexes. Just as the polyhedral product unifies various constructions of spaces across different fields, the polyhedral join product construction unifies various constructions of simplicial complexes. In [Reference Ewald13], the concept of the simplicial wedge construction for toric varieties was introduced, and this construction was first considered in regard to the polyhedral product in [Reference Bahri, Bendersky, Cohen and Gitler7]. This was then generalised in [Reference Ayzenberg4] to the composition complex (at the time, this was named the substitution complex, but has since changed). The composition complex has applications in topological data analysis [Reference Kara18]. This construction is similar, but different to the substitution complex in [Reference Abramyan and Panov1], where it was shown that specific substitution complexes are the smallest simplicial complexes that realise iterated higher Whitehead products. Substitution complexes have also been considered in geometric group theory [Reference Davis and Okun11]. Recently, a specific example of the substitution complex was used to prove a stability theorem for bigraded persistent double homology [Reference Bahri, Limonchenko, Panov, Song and Stanley8]. Both the substitution complex and the construction complex are specific examples of polyhedral join products, which were first defined in [Reference Ayzenberg4]. Polyhedral products and polyhedral join products have a nice relation, as characterised in [Reference Vidaurre28] (Theorem 2.9). Recently, Steenrod operations with relation to polyhedral join products have been explored [Reference Agarwal, Grbić, Intermont, Jovanović, Lagoda and Whitehouse2].
In this paper, we obtain a homotopy equivalence for  $\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}}$. To do this, we utilise facts about the underlying simplicial complex
$\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}}$. To do this, we utilise facts about the underlying simplicial complex ![]() $M$. Recall that the link of a vertex is the subcomplex
$M$. Recall that the link of a vertex is the subcomplex ![]() $\mathrm{lk}_M(v) = \{\tau \in M | \{v\} \cap \tau = \emptyset, \{v\} \cup \tau \in K\}$ and the restriction of a vertex is the subcomplex
$\mathrm{lk}_M(v) = \{\tau \in M | \{v\} \cap \tau = \emptyset, \{v\} \cup \tau \in K\}$ and the restriction of a vertex is the subcomplex ![]() $M \setminus v = \{\tau \in M | \{v\} \cap \tau = \emptyset\}$.
$M \setminus v = \{\tau \in M | \{v\} \cap \tau = \emptyset\}$.
Theorem 1.1. Let  ${(\underline{K},\underline{L})}^{*M}$ be a polyhedral join product, where each
${(\underline{K},\underline{L})}^{*M}$ be a polyhedral join product, where each ![]() $L_i \subseteq K_i$ is a subcomplex of
$L_i \subseteq K_i$ is a subcomplex of ![]() $K_i$. There is a homotopy equivalence
$K_i$. There is a homotopy equivalence
 \begin{equation*}\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \simeq \prod_{i=1}^m \Omega {(\underline{X},\underline{A})}^{K_i} \times \prod_{i=k}^m \Omega (G_i*H_i)\end{equation*}
\begin{equation*}\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \simeq \prod_{i=1}^m \Omega {(\underline{X},\underline{A})}^{K_i} \times \prod_{i=k}^m \Omega (G_i*H_i)\end{equation*} where ![]() $G_i$ is the homotopy fibre of the map
$G_i$ is the homotopy fibre of the map  ${(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*\mathrm{lk}_{M\setminus \{m,\dots,i+1\}}(i)}} \to {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus \{m,\dots,i\}}}$,
${(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*\mathrm{lk}_{M\setminus \{m,\dots,i+1\}}(i)}} \to {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus \{m,\dots,i\}}}$, ![]() $H_i$ is the homotopy fibre of the map
$H_i$ is the homotopy fibre of the map  ${(\underline{X},\underline{A})}^{L_i} \to {(\underline{X},\underline{A})}^{K_i}$ where
${(\underline{X},\underline{A})}^{L_i} \to {(\underline{X},\underline{A})}^{K_i}$ where ![]() $L_i$ is considered on the vertex set of
$L_i$ is considered on the vertex set of ![]() $K_i$, and
$K_i$, and ![]() $k \in [m]$ is such that
$k \in [m]$ is such that ![]() $M \setminus \{m,\dots,k\}$ is a simplex.
$M \setminus \{m,\dots,k\}$ is a simplex.
Such a homotopy equivalence allows us to explore the homotopy type of  $\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}}$, which is the second problem motivating this work.
$\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}}$, which is the second problem motivating this work.
Let ![]() ${\mathcal{P}}$ be the full subcategory of topological spaces that are homotopy equivalent to a finite type product of spheres and loops on spheres. We can then consider when
${\mathcal{P}}$ be the full subcategory of topological spaces that are homotopy equivalent to a finite type product of spheres and loops on spheres. We can then consider when  $\Omega {(\underline{X},\underline{A})}^K$ belongs to
$\Omega {(\underline{X},\underline{A})}^K$ belongs to ![]() ${\mathcal{P}}$. This is part of a wider body of work investigating Anick’s conjecture. Anick’s conjecture states that if a space
${\mathcal{P}}$. This is part of a wider body of work investigating Anick’s conjecture. Anick’s conjecture states that if a space ![]() $X$ is a finite, connected
$X$ is a finite, connected ![]() $CW$-complex, then localised at almost all primes
$CW$-complex, then localised at almost all primes ![]() $p$,
$p$, ![]() $\Omega X$ decomposes as a finite type product of spheres, loops on spheres and indecomposable space related to Moore spaces. Currently, there are two known types of simplicial complexes that give rise to polyhedral products such that
$\Omega X$ decomposes as a finite type product of spheres, loops on spheres and indecomposable space related to Moore spaces. Currently, there are two known types of simplicial complexes that give rise to polyhedral products such that  $\Omega {(\underline{CA},\underline{A})}^{K} \in {\mathcal{P}}$; that is to say, they verify Anick’s conjecture without the need to localise. One type is simplicial complexes such that the associated polyhedral product
$\Omega {(\underline{CA},\underline{A})}^{K} \in {\mathcal{P}}$; that is to say, they verify Anick’s conjecture without the need to localise. One type is simplicial complexes such that the associated polyhedral product  ${(\underline{CA},\underline{A})}^K$ belongs to the collection of topological spaces which are homotopy equivalent to a finite type wedge of spheres, denoted
${(\underline{CA},\underline{A})}^K$ belongs to the collection of topological spaces which are homotopy equivalent to a finite type wedge of spheres, denoted ![]() ${\mathcal{W}}$. Much progress has been made in determining which families of simplicial complexes give rise to such polyhedral products. For example, when
${\mathcal{W}}$. Much progress has been made in determining which families of simplicial complexes give rise to such polyhedral products. For example, when ![]() $K$ is shifted [Reference Grbić and Theriault16], flag with chordal
$K$ is shifted [Reference Grbić and Theriault16], flag with chordal ![]() $1$-skeleton [Reference Grbić, Panov, Theriault and Wu14], and most generally, a totally fillable complex [Reference Iriye and Kishimoto17], then
$1$-skeleton [Reference Grbić, Panov, Theriault and Wu14], and most generally, a totally fillable complex [Reference Iriye and Kishimoto17], then  ${(\underline{CA},\underline{A})}^K \in {\mathcal{W}}$. If
${(\underline{CA},\underline{A})}^K \in {\mathcal{W}}$. If  ${(\underline{CA},\underline{A})}^K \in {\mathcal{W}}$, then the Hilton-Milnor theorem implies that
${(\underline{CA},\underline{A})}^K \in {\mathcal{W}}$, then the Hilton-Milnor theorem implies that  $\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$. Many polyhedral products are not wedges of spheres, but their loop space belongs to
$\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$. Many polyhedral products are not wedges of spheres, but their loop space belongs to ![]() ${\mathcal{P}}$, and recently, much progress in this area has been made. [Reference Stanton23] showed that when
${\mathcal{P}}$, and recently, much progress in this area has been made. [Reference Stanton23] showed that when ![]() $K$ is the
$K$ is the ![]() $k$-skeleton of a flag complex,
$k$-skeleton of a flag complex,  $\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$ and in[Reference Vylegzhanin29] an explicit loop space decomposition was given. Furthermore, in [Reference Stanton24], it was shown that
$\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$ and in[Reference Vylegzhanin29] an explicit loop space decomposition was given. Furthermore, in [Reference Stanton24], it was shown that  $\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$ if and only if each full subcomplex
$\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$ if and only if each full subcomplex ![]() $K_I$ with a complete 1-skeleton is such that
$K_I$ with a complete 1-skeleton is such that  $\Omega {(\underline{CA},\underline{A})}^{K_I} \in {\mathcal{P}}$. However, the polyhedral join product produces large simplicial complexes, and it is hard to classify all subcomplexes with a complete
$\Omega {(\underline{CA},\underline{A})}^{K_I} \in {\mathcal{P}}$. However, the polyhedral join product produces large simplicial complexes, and it is hard to classify all subcomplexes with a complete ![]() $1$-skeleton, so a different approach is required. For the polyhedral join product, we prove the following.
$1$-skeleton, so a different approach is required. For the polyhedral join product, we prove the following.
Theorem 1.2. Let ![]() $M$ be a simplicial complex on
$M$ be a simplicial complex on ![]() $[m]$ vertices. Let
$[m]$ vertices. Let  ${(\underline{K},\underline{L})}^{*M}$ be a polyhedral join product where
${(\underline{K},\underline{L})}^{*M}$ be a polyhedral join product where ![]() $K_i$ is a simplicial complex on the vertex set
$K_i$ is a simplicial complex on the vertex set ![]() $[k_i]$ for
$[k_i]$ for ![]() $i \in [m]$, and each
$i \in [m]$, and each ![]() $L_i \subseteq K_i$ is a subcomplex of
$L_i \subseteq K_i$ is a subcomplex of ![]() $K_i$. Let
$K_i$. Let ![]() ${(\underline{CA},\underline{A})}$ be a sequence of pairs
${(\underline{CA},\underline{A})}$ be a sequence of pairs ![]() $(CA_j,A_j)$ where
$(CA_j,A_j)$ where ![]() $1 \leq j \leq k_1 + \dots + k_m$. Suppose
$1 \leq j \leq k_1 + \dots + k_m$. Suppose ![]() $\Sigma A_j \in {\mathcal{W}}$ for all
$\Sigma A_j \in {\mathcal{W}}$ for all ![]() $j$. For all
$j$. For all ![]() $i \in [m]$, let
$i \in [m]$, let ![]() $H_i$ be the homotopy fibre of the map
$H_i$ be the homotopy fibre of the map  ${(\underline{CA},\underline{A})}^{L_i} \to {(\underline{CA},\underline{A})}^{K_i}$, where
${(\underline{CA},\underline{A})}^{L_i} \to {(\underline{CA},\underline{A})}^{K_i}$, where ![]() $L_i$ is considered to be on the vertex set of
$L_i$ is considered to be on the vertex set of ![]() $K_i$. If
$K_i$. If  $\Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{P}}$ and
$\Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{P}}$ and ![]() $\Sigma H_i \in {\mathcal{W}}$ for each
$\Sigma H_i \in {\mathcal{W}}$ for each ![]() $i \in [m]$, then
$i \in [m]$, then  $\Omega {(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$.
$\Omega {(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$.
Theorem 1.2 gives the conditions under which polyhedral products associated with polyhedral join products verify Anick’s conjecture; conditions that depend on the pairs ![]() ${(\underline{K},\underline{L})}$ and the polyhedral product
${(\underline{K},\underline{L})}$ and the polyhedral product  ${(\underline{CA},\underline{A})}^M$. We use Theorem 1.2 in Section 7 to generate new families of simplicial complexes such that
${(\underline{CA},\underline{A})}^M$. We use Theorem 1.2 in Section 7 to generate new families of simplicial complexes such that ![]() $\Omega {\mathcal{Z}}_{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$, but the simplicial complex
$\Omega {\mathcal{Z}}_{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$, but the simplicial complex  ${(\underline{K},\underline{L})}^{*M}$ is not the
${(\underline{K},\underline{L})}^{*M}$ is not the ![]() $k$-skeleton of a flag complex, or such that
$k$-skeleton of a flag complex, or such that ![]() ${\mathcal{Z}}_{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{W}}$. To do this, we analyse the substitution complex.
${\mathcal{Z}}_{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{W}}$. To do this, we analyse the substitution complex.
The structure of this paper is as follows. In Section 2, we cover some preliminary results, and in Section 3, we prove many combinatorial results concerning the polyhedral join product. In Section 4, we prove a homotopy equivalence concerning polyhedral products, and in Section 5, we apply this to the polyhedral join product. In Section 6, we consider when the polyhedral join product preserves the property of  $\Omega {(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$. Finally, in Section 7, we define new families of simplicial complexes for which
$\Omega {(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$. Finally, in Section 7, we define new families of simplicial complexes for which  $\Omega {(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$.
$\Omega {(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$.
2. Preliminary results
2.1. Properties of  ${\mathcal{W}}$ and
${\mathcal{W}}$ and  ${\mathcal{P}}$
${\mathcal{P}}$
Let ![]() ${\mathcal{W}}$ denote the collection of topological spaces that are homotopy equivalent to a finite type wedge of spheres
${\mathcal{W}}$ denote the collection of topological spaces that are homotopy equivalent to a finite type wedge of spheres ![]() $S^n$, where
$S^n$, where ![]() $n \geq2$, and let
$n \geq2$, and let ![]() ${\mathcal{P}}$ be the collection of
${\mathcal{P}}$ be the collection of ![]() $H$-spaces which are homotopy equivalent to a finite type product of spheres and loops on simply connected spheres. The relations between spaces in
$H$-spaces which are homotopy equivalent to a finite type product of spheres and loops on simply connected spheres. The relations between spaces in ![]() ${\mathcal{P}}$ and
${\mathcal{P}}$ and ![]() ${\mathcal{W}}$ proved in this section will be used throughout the paper. We begin by stating several results, the first of which is the Hilton-Milnor Theorem. Let
${\mathcal{W}}$ proved in this section will be used throughout the paper. We begin by stating several results, the first of which is the Hilton-Milnor Theorem. Let ![]() $X^{\wedge i}$ denote the
$X^{\wedge i}$ denote the ![]() $i$-fold smash product of
$i$-fold smash product of ![]() $X$.
$X$.
Theorem 2.1 (Hilton-Milnor)
[Reference Milnor, Adams and Shepherd21] Let ![]() $X$ and
$X$ and ![]() $Y$ be pointed spaces. There is a homotopy equivalence
$Y$ be pointed spaces. There is a homotopy equivalence
 \begin{equation*}\Omega( \Sigma X \vee \Sigma Y) \simeq \Omega \Sigma X \times \ \Omega \Sigma \big( \bigvee_{i,j \geq 1} X^{\wedge i} \wedge Y^{\wedge j} \big).\end{equation*}
\begin{equation*}\Omega( \Sigma X \vee \Sigma Y) \simeq \Omega \Sigma X \times \ \Omega \Sigma \big( \bigvee_{i,j \geq 1} X^{\wedge i} \wedge Y^{\wedge j} \big).\end{equation*}Lemma 2.2. If ![]() $X \in {\mathcal{W}}$, then
$X \in {\mathcal{W}}$, then ![]() $\Omega {X} \in {\mathcal{P}}.$
$\Omega {X} \in {\mathcal{P}}.$
The following two lemmas are well-known results. For proofs, see [Reference Theriault27, Lemma 4.1] and [Reference Amelotte3, Lemma 3.1], respectively.
Lemma 2.3. If ![]() $X \in {\mathcal{P}}$ then
$X \in {\mathcal{P}}$ then ![]() $\Sigma X \in {\mathcal{W}}.$
$\Sigma X \in {\mathcal{W}}.$
Recall that a space ![]() $A$ is a retract of
$A$ is a retract of ![]() $X$ if there are maps
$X$ if there are maps ![]() $f: A \to X$ and
$f: A \to X$ and ![]() $g: X \to A$ such that
$g: X \to A$ such that ![]() $g \circ f$ is the identity.
$g \circ f$ is the identity.
Lemma 2.4. Suppose ![]() $X \in {\mathcal{W}}$, and let
$X \in {\mathcal{W}}$, and let ![]() $A$ be a retract of
$A$ be a retract of ![]() $X$. Then
$X$. Then ![]() $A \in {\mathcal{W}}.$
$A \in {\mathcal{W}}.$
The following two lemmas concern the homotopy type of retracts of spaces.
Lemma 2.5. ([Reference Stanton23, Theorem 3.10])
Let ![]() $X \in {\mathcal{P}}$, and let
$X \in {\mathcal{P}}$, and let ![]() $A$ be a space which retracts of
$A$ be a space which retracts of ![]() $X$. Then
$X$. Then ![]() $A \in {\mathcal{P}}.$
$A \in {\mathcal{P}}.$
Lemma 2.6. Let ![]() $X$ be a pointed
$X$ be a pointed ![]() $CW$-complex, and suppose
$CW$-complex, and suppose ![]() $\Omega \Sigma X \in {\mathcal{P}}$. Then
$\Omega \Sigma X \in {\mathcal{P}}$. Then ![]() $\Sigma X \in {\mathcal{W}}$.
$\Sigma X \in {\mathcal{W}}$.
Proof. It is well known that if ![]() $Y$ is a co-
$Y$ is a co-![]() $H$ space, then
$H$ space, then ![]() $Y$ retracts of
$Y$ retracts of ![]() $\Sigma \Omega Y$. First note that as
$\Sigma \Omega Y$. First note that as ![]() $\Omega \Sigma X \in {\mathcal{P}}$, we obtain
$\Omega \Sigma X \in {\mathcal{P}}$, we obtain ![]() $\Sigma \Omega \Sigma X \in {\mathcal{W}}$ by Lemma 2.3. Although
$\Sigma \Omega \Sigma X \in {\mathcal{W}}$ by Lemma 2.3. Although ![]() $X$ may not be a co-
$X$ may not be a co-![]() $H$ space,
$H$ space, ![]() $\Sigma X$ is, and so
$\Sigma X$ is, and so ![]() $\Sigma X$ retracts off
$\Sigma X$ retracts off ![]() $\Sigma \Omega \Sigma X$. As
$\Sigma \Omega \Sigma X$. As ![]() $\Sigma X$ retracts off a space in
$\Sigma X$ retracts off a space in ![]() ${\mathcal{W}}$, by Lemma 2.4
${\mathcal{W}}$, by Lemma 2.4 ![]() $\Sigma X \in {\mathcal{W}}$.
$\Sigma X \in {\mathcal{W}}$.
2.2. Polyhedral products
In this subsection, we cover some essential results concerning polyhedral products and loop space decompositions of polyhedral products. We begin by stating some fundamental properties of polyhedral products relating to the underlying simplicial complex. Recall that the join of two simplicial complexes ![]() $K_1$ and
$K_1$ and ![]() $K_2$ is the simplicial complex
$K_2$ is the simplicial complex
The following lemma follows from this definition and the definition of the polyhedral product.
Lemma 2.7. ([Reference Buchstaber and Panov10, Proposition 4.2.5])
Let ![]() $K = K_1 * K_2$, where
$K = K_1 * K_2$, where ![]() $K_1$ is on the vertex set
$K_1$ is on the vertex set ![]() $\{1,\dots,l\}$ and
$\{1,\dots,l\}$ and ![]() $K_2$ is on the vertex set
$K_2$ is on the vertex set ![]() $\{l+1,\dots,m\}$. Then
$\{l+1,\dots,m\}$. Then
 \begin{equation*}
{(\underline{X},\underline{A})}^{K} = {(\underline{X},\underline{A})}^{K_1} \times {(\underline{X},\underline{A})}^{K_2}.
\end{equation*}
\begin{equation*}
{(\underline{X},\underline{A})}^{K} = {(\underline{X},\underline{A})}^{K_1} \times {(\underline{X},\underline{A})}^{K_2}.
\end{equation*} Let ![]() $L$ be a simplicial complex on the vertex set
$L$ be a simplicial complex on the vertex set ![]() $[l]$, where
$[l]$, where ![]() $l \leq m$. Let
$l \leq m$. Let ![]() $\overline{L}$ be the simplicial complex on the vertex set
$\overline{L}$ be the simplicial complex on the vertex set ![]() $[m]$ by considering the elements of
$[m]$ by considering the elements of ![]() $[m]$ that are not vertices of
$[m]$ that are not vertices of ![]() $L$ as ghost vertices.
$L$ as ghost vertices.
Proposition 2.8. ([Reference Grbić and Theriault16, Proposition 3.1])
Let ![]() $K$ be a simplicial complex on the vertex set
$K$ be a simplicial complex on the vertex set ![]() $[m]$, and suppose
$[m]$, and suppose ![]() $K = K_1 \cup_L K_2$, that is,
$K = K_1 \cup_L K_2$, that is, ![]() $K$ is a pushout of
$K$ is a pushout of ![]() $K_1$ and
$K_1$ and ![]() $K_2$ over
$K_2$ over ![]() $L$. Then, by regarding
$L$. Then, by regarding ![]() $\overline{L}$,
$\overline{L}$, ![]() $\overline{K_1}$,
$\overline{K_1}$, ![]() $\overline{K_2}$ as simplicial complexes on the vertex set
$\overline{K_2}$ as simplicial complexes on the vertex set ![]() $[m]$, there is a pushout of polyhedral products
$[m]$, there is a pushout of polyhedral products

Let ![]() $K$ be a simplicial complex on the vertex set
$K$ be a simplicial complex on the vertex set ![]() $[m]$. For a vertex
$[m]$. For a vertex ![]() $v \in K$, the star, restriction and link of
$v \in K$, the star, restriction and link of ![]() $v$ are the subcomplexes
$v$ are the subcomplexes
From the above definitions, for each vertex ![]() $i \in [m]$, there is a pushout of simplicial complexes
$i \in [m]$, there is a pushout of simplicial complexes

As ![]() $\mathrm{st}_K(i) = \mathrm{lk}_K(i) * i$, by Lemma 2.7, we can rewrite
$\mathrm{st}_K(i) = \mathrm{lk}_K(i) * i$, by Lemma 2.7, we can rewrite  ${(\underline{X},\underline{A})}^{\mathrm{st}_K(i)}$ as
${(\underline{X},\underline{A})}^{\mathrm{st}_K(i)}$ as  ${(\underline{X},\underline{A})}^{\mathrm{lk}_K(i)} \times X_i$. Applying Proposition 2.8, we obtain the following result.
${(\underline{X},\underline{A})}^{\mathrm{lk}_K(i)} \times X_i$. Applying Proposition 2.8, we obtain the following result.
Corollary 2.9. For each vertex ![]() $i \in [m]$ there is a pushout
$i \in [m]$ there is a pushout

where ![]() $\mathrm{lk}_K(i)$ is regarded as a simplicial complex on the vertex set of
$\mathrm{lk}_K(i)$ is regarded as a simplicial complex on the vertex set of ![]() $K \setminus i$.
$K \setminus i$.
We now give some results concerning a specific type of subcomplex. The subcomplex ![]() $L$ is a full subcomplex of
$L$ is a full subcomplex of ![]() $K$ if every face in
$K$ if every face in ![]() $K$ on the vertex set
$K$ on the vertex set ![]() $[l]$ is also a face of
$[l]$ is also a face of ![]() $L$. We denote a full subcomplex on a set
$L$. We denote a full subcomplex on a set ![]() $I \subseteq [m]$ as
$I \subseteq [m]$ as ![]() $K_I$.
$K_I$.
Lemma 2.10. ([Reference Denham and Suciu12, Lemma 2.2.3])
Let ![]() $K$ be a simplicial complex on the vertex set
$K$ be a simplicial complex on the vertex set ![]() $[m]$ and let
$[m]$ and let ![]() $L$ be a full subcomplex of
$L$ be a full subcomplex of ![]() $K$ on the vertex set
$K$ on the vertex set ![]() $[l]$. Then the induced map of polyhedral products
$[l]$. Then the induced map of polyhedral products  ${(\underline{X},\underline{A})}^L \to {(\underline{X},\underline{A})}^K$ has a left inverse
${(\underline{X},\underline{A})}^L \to {(\underline{X},\underline{A})}^K$ has a left inverse
 \begin{equation*}r: {(\underline{X},\underline{A})}^K \to {(\underline{X},\underline{A})}^L.
\end{equation*}
\begin{equation*}r: {(\underline{X},\underline{A})}^K \to {(\underline{X},\underline{A})}^L.
\end{equation*}Lemma 2.11. If  $\Omega {(\underline{X},\underline{A})}^K \in {\mathcal{P}}$, then for any full subcomplex
$\Omega {(\underline{X},\underline{A})}^K \in {\mathcal{P}}$, then for any full subcomplex ![]() $K_I$ of
$K_I$ of ![]() $K$, we have
$K$, we have  $\Omega {(\underline{X},\underline{A})}^{K_I} \in {\mathcal{P}}$.
$\Omega {(\underline{X},\underline{A})}^{K_I} \in {\mathcal{P}}$.
Proof. By Lemma 2.10  $\Omega {(\underline{X},\underline{A})}^{K_I}$ is a retract of
$\Omega {(\underline{X},\underline{A})}^{K_I}$ is a retract of  $\Omega {(\underline{X},\underline{A})}^K$, and so by Lemma 2.5, we have
$\Omega {(\underline{X},\underline{A})}^K$, and so by Lemma 2.5, we have  $\Omega {(\underline{X},\underline{A})}^{K_I} \in {\mathcal{P}}$.
$\Omega {(\underline{X},\underline{A})}^{K_I} \in {\mathcal{P}}$.
Lemma 2.12. Let ![]() $L$ be a full subcomplex of
$L$ be a full subcomplex of ![]() $K$, and let
$K$, and let  $\Omega {(\underline{X},\underline{A})}^K \in {\mathcal{P}}$. If
$\Omega {(\underline{X},\underline{A})}^K \in {\mathcal{P}}$. If ![]() $F$ is the homotopy fibre of the map
$F$ is the homotopy fibre of the map  ${(\underline{X},\underline{A})}^L \to {(\underline{X},\underline{A})}^K$, then
${(\underline{X},\underline{A})}^L \to {(\underline{X},\underline{A})}^K$, then ![]() $\Sigma F \in {\mathcal{W}}$.
$\Sigma F \in {\mathcal{W}}$.
Proof. As ![]() $L$ is a full subcomplex of
$L$ is a full subcomplex of ![]() $K$, the map
$K$, the map  ${(\underline{X},\underline{A})}^{L} \to {(\underline{X},\underline{A})}^{K}$ has a left homotopy inverse by Lemma 2.10, and so the connecting map
${(\underline{X},\underline{A})}^{L} \to {(\underline{X},\underline{A})}^{K}$ has a left homotopy inverse by Lemma 2.10, and so the connecting map  $\delta: \Omega {(\underline{X},\underline{A})}^{K} \to F$ has a right homotopy inverse. Therefore, the homotopy fibration sequence
$\delta: \Omega {(\underline{X},\underline{A})}^{K} \to F$ has a right homotopy inverse. Therefore, the homotopy fibration sequence  $\Omega {(\underline{X},\underline{A})}^{L} \to \Omega {(\underline{X},\underline{A})}^{K} \xrightarrow{\delta} F$ splits to give a homotopy equivalence
$\Omega {(\underline{X},\underline{A})}^{L} \to \Omega {(\underline{X},\underline{A})}^{K} \xrightarrow{\delta} F$ splits to give a homotopy equivalence  $\Omega {(\underline{X},\underline{A})}^{K} \simeq \Omega {(\underline{X},\underline{A})}^{L} \times F$. As
$\Omega {(\underline{X},\underline{A})}^{K} \simeq \Omega {(\underline{X},\underline{A})}^{L} \times F$. As  $\Omega {(\underline{X},\underline{A})}^{K} \in {\mathcal{P}}$,
$\Omega {(\underline{X},\underline{A})}^{K} \in {\mathcal{P}}$, ![]() $F$ must therefore be in
$F$ must therefore be in ![]() ${\mathcal{P}}$ by Lemma 2.5. By Lemma 2.3,
${\mathcal{P}}$ by Lemma 2.5. By Lemma 2.3, ![]() $\Sigma F$ must therefore be in
$\Sigma F$ must therefore be in ![]() ${\mathcal{W}}$.
${\mathcal{W}}$.
Lemma 2.13. ([Reference Theriault25, Theorem 9.4])
Let ![]() $G_i$ be the homotopy fibre of the map
$G_i$ be the homotopy fibre of the map  ${(\underline{X},\underline{A})}^{\mathrm{lk}_{K\setminus \{m,\dots,i+1\}}(i)} \to {(\underline{X},\underline{A})}^{K \setminus \{m,\dots,i\} }$, and let
${(\underline{X},\underline{A})}^{\mathrm{lk}_{K\setminus \{m,\dots,i+1\}}(i)} \to {(\underline{X},\underline{A})}^{K \setminus \{m,\dots,i\} }$, and let ![]() $Y_i$ be the homotopy fibre of the map
$Y_i$ be the homotopy fibre of the map ![]() $A_i \to X_i$. Then there is a homotopy equivalence
$A_i \to X_i$. Then there is a homotopy equivalence
 \begin{equation*}\Omega {(\underline{X},\underline{A})}^K \simeq \prod_{i=1}^m \Omega X_i \times \prod_{i=1}^m \Omega (\Sigma G_i \wedge Y_i). \end{equation*}
\begin{equation*}\Omega {(\underline{X},\underline{A})}^K \simeq \prod_{i=1}^m \Omega X_i \times \prod_{i=1}^m \Omega (\Sigma G_i \wedge Y_i). \end{equation*} We can apply this Lemma to determine when the homotopy fibre of ![]() $\Sigma^k G_m \in {\mathcal{W}}$.
$\Sigma^k G_m \in {\mathcal{W}}$.
Lemma 2.14. Let ![]() $K$ be a simplicial complex on the vertex set
$K$ be a simplicial complex on the vertex set ![]() $[m]$. Let
$[m]$. Let  $\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$, and let
$\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$, and let ![]() $G_m$ denote the homotopy fibre of the map
$G_m$ denote the homotopy fibre of the map  ${(\underline{CA},\underline{A})}^{\mathrm{lk}_{K}(m)} \to {(\underline{CA},\underline{A})}^{K \setminus m}$. Suppose
${(\underline{CA},\underline{A})}^{\mathrm{lk}_{K}(m)} \to {(\underline{CA},\underline{A})}^{K \setminus m}$. Suppose ![]() $A_m$ is
$A_m$ is ![]() $(k-1)$-connected. If
$(k-1)$-connected. If ![]() $\Sigma A_m \in {\mathcal{W}}$, then
$\Sigma A_m \in {\mathcal{W}}$, then ![]() $\Sigma^{k} G_m \in {\mathcal{W}}$.
$\Sigma^{k} G_m \in {\mathcal{W}}$.
Proof. By Lemma 2.13 we have that
 \begin{equation*}\Omega {(\underline{CA},\underline{A})}^K \simeq \Omega {(\underline{CA},\underline{A})}^{K \setminus m} \times \Omega \Sigma (G_m \wedge A_m).\end{equation*}
\begin{equation*}\Omega {(\underline{CA},\underline{A})}^K \simeq \Omega {(\underline{CA},\underline{A})}^{K \setminus m} \times \Omega \Sigma (G_m \wedge A_m).\end{equation*} As  $\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$, by Lemma 2.5 we have
$\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$, by Lemma 2.5 we have ![]() $\Omega (\Sigma G_m \wedge A_m) \in {\mathcal{P}}$. By Lemma 2.6,
$\Omega (\Sigma G_m \wedge A_m) \in {\mathcal{P}}$. By Lemma 2.6, ![]() $\Sigma G_m \wedge A_m \in {\mathcal{W}}$. As
$\Sigma G_m \wedge A_m \in {\mathcal{W}}$. As ![]() $\Sigma A_m \in {\mathcal{W}}$ by hypothesis,
$\Sigma A_m \in {\mathcal{W}}$ by hypothesis, ![]() $\Sigma A_m$ is homotopy equivalent to
$\Sigma A_m$ is homotopy equivalent to  $\bigvee_{j \in \alpha} S^j$ for some indexing set
$\bigvee_{j \in \alpha} S^j$ for some indexing set ![]() $\alpha$. Therefore,
$\alpha$. Therefore,
 \begin{equation*}\Sigma G_m \wedge A_m \simeq \bigvee_{j \in \alpha} G_m \wedge S^j \simeq \bigvee_{j \in \alpha} \Sigma^{j} G_m.\end{equation*}
\begin{equation*}\Sigma G_m \wedge A_m \simeq \bigvee_{j \in \alpha} G_m \wedge S^j \simeq \bigvee_{j \in \alpha} \Sigma^{j} G_m.\end{equation*} As each ![]() $\Sigma^j G_m$ is retracting off
$\Sigma^j G_m$ is retracting off ![]() $\Sigma G_m \wedge A_m$, we have
$\Sigma G_m \wedge A_m$, we have ![]() $\Sigma^j G_m \in {\mathcal{W}}$ by Lemma 2.4. Furthermore, as
$\Sigma^j G_m \in {\mathcal{W}}$ by Lemma 2.4. Furthermore, as ![]() $A_m$ is
$A_m$ is ![]() $(k-1)$-connected,
$(k-1)$-connected, ![]() $\Sigma A_m$ is
$\Sigma A_m$ is ![]() $k$-connected. Therefore, the smallest
$k$-connected. Therefore, the smallest ![]() $j \in \alpha$ is
$j \in \alpha$ is ![]() $k$, and so
$k$, and so ![]() $\Sigma^k G_m \in {\mathcal{W}}$.
$\Sigma^k G_m \in {\mathcal{W}}$.
Lemma 2.15. Let ![]() $K$ be a simplicial complex on the vertex set
$K$ be a simplicial complex on the vertex set ![]() $[m]$. If
$[m]$. If ![]() ${(\underline{CA},\underline{A})}$ is a sequence of pairs of spaces where each
${(\underline{CA},\underline{A})}$ is a sequence of pairs of spaces where each ![]() $A_i$ is at least
$A_i$ is at least ![]() $(k-1)$-connected for some
$(k-1)$-connected for some ![]() $k$, then
$k$, then  ${(\underline{CA},\underline{A})}^K$ is at least
${(\underline{CA},\underline{A})}^K$ is at least ![]() $(2k-2)$-connected.
$(2k-2)$-connected.
Proof. After suspending, by [Reference Bahri, Bendersky, Cohen and Gitler6, Theorem 2.21] there is a homotopy equivalence
 \begin{equation*}\Sigma {(\underline{CA},\underline{A})}^K \simeq \Sigma \bigvee_{I \notin K} |K_I|*\widehat{A}^I\end{equation*}
\begin{equation*}\Sigma {(\underline{CA},\underline{A})}^K \simeq \Sigma \bigvee_{I \notin K} |K_I|*\widehat{A}^I\end{equation*} where ![]() $|K_I|$ is the geometric realisation of the full subcomplex on the vertex set
$|K_I|$ is the geometric realisation of the full subcomplex on the vertex set ![]() $I$, and
$I$, and ![]() $\widehat{A}^I$ is the iterated smash product
$\widehat{A}^I$ is the iterated smash product ![]() $A_{i_1} \wedge \dots \wedge A_{i_I}$. By assumption
$A_{i_1} \wedge \dots \wedge A_{i_I}$. By assumption ![]() $\mathrm{conn}(A_i) \geq k-1$ for all
$\mathrm{conn}(A_i) \geq k-1$ for all ![]() $i \in [m]$, and so the connectivity of
$i \in [m]$, and so the connectivity of ![]() $\widehat{A}^I$ is at least
$\widehat{A}^I$ is at least ![]() $k|I| - 1$. Therefore, the connectivity of
$k|I| - 1$. Therefore, the connectivity of  $|K_I|*\widehat{A}^I \simeq \Sigma |K_I| \wedge \widehat{A}^I$ is at least
$|K_I|*\widehat{A}^I \simeq \Sigma |K_I| \wedge \widehat{A}^I$ is at least ![]() $\mathrm{conn}(|K_I|) + k|I| + 1$. This is minimised when
$\mathrm{conn}(|K_I|) + k|I| + 1$. This is minimised when ![]() $|I|=2$, in which case
$|I|=2$, in which case ![]() $|K_I| \simeq S^0$. Therefore, the lower bound for the connectivity of
$|K_I| \simeq S^0$. Therefore, the lower bound for the connectivity of  $|K_I|*\widehat{A}^I$ is
$|K_I|*\widehat{A}^I$ is ![]() $2k-1$, and so
$2k-1$, and so  $\Sigma {(\underline{CA},\underline{A})}^K$ is at least
$\Sigma {(\underline{CA},\underline{A})}^K$ is at least ![]() $(2k-1)$-connected. After desuspending, we obtain
$(2k-1)$-connected. After desuspending, we obtain  ${(\underline{CA},\underline{A})}^K$ is at least
${(\underline{CA},\underline{A})}^K$ is at least ![]() $(2k-2)$-connected.
$(2k-2)$-connected.
Corollary 2.16. Let ![]() $\overline{L}$ be a simplicial complex on the vertex set
$\overline{L}$ be a simplicial complex on the vertex set ![]() $[m]$ with ghost vertices. If
$[m]$ with ghost vertices. If ![]() ${(\underline{CA},\underline{A})}$ is a sequence of pairs of spaces where each
${(\underline{CA},\underline{A})}$ is a sequence of pairs of spaces where each ![]() $A_i$ is at least
$A_i$ is at least ![]() $(k-1)$-connected for some
$(k-1)$-connected for some ![]() $k$, then
$k$, then  ${(\underline{CA},\underline{A})}^{\overline{L}}$ is at least
${(\underline{CA},\underline{A})}^{\overline{L}}$ is at least ![]() $(k-1)$-connected.
$(k-1)$-connected.
Proof. Note that there is an equality
 \begin{equation*}{(\underline{CA},\underline{A})}^{\overline{L}} = {(\underline{CA},\underline{A})}^L \times \prod_{i \notin L} A_i\end{equation*}
\begin{equation*}{(\underline{CA},\underline{A})}^{\overline{L}} = {(\underline{CA},\underline{A})}^L \times \prod_{i \notin L} A_i\end{equation*}that follows from the definition of the polyhedral product. The lower bound for connectivity immediately follows.
Lemma 2.17. Let ![]() $K$ be a simplicial complex with no ghost vertices, and let
$K$ be a simplicial complex with no ghost vertices, and let ![]() $L$ be a subcomplex of
$L$ be a subcomplex of ![]() $K$. Let
$K$. Let ![]() $H$ be the homotopy fibre of the map
$H$ be the homotopy fibre of the map  ${(\underline{CA},\underline{A})}^{\overline{L}} \to {(\underline{CA},\underline{A})}^K$. Suppose that each
${(\underline{CA},\underline{A})}^{\overline{L}} \to {(\underline{CA},\underline{A})}^K$. Suppose that each ![]() $A_i$ is at least
$A_i$ is at least ![]() $(k-1)$-connected. Then
$(k-1)$-connected. Then ![]() $H$ is at least
$H$ is at least ![]() $(k-1)$-connected.
$(k-1)$-connected.
Proof. The fibration sequence  $H \to {(\underline{CA},\underline{A})}^{\overline{L}} \to {(\underline{CA},\underline{A})}^K$ induces a long exact sequence of homotopy groups. By Lemma 2.15 and Corollary 2.16 we obtain
$H \to {(\underline{CA},\underline{A})}^{\overline{L}} \to {(\underline{CA},\underline{A})}^K$ induces a long exact sequence of homotopy groups. By Lemma 2.15 and Corollary 2.16 we obtain  $\pi_n({(\underline{CA},\underline{A})}^K) = 0$ for
$\pi_n({(\underline{CA},\underline{A})}^K) = 0$ for ![]() $n \leq 2k-2$ and
$n \leq 2k-2$ and  $\pi_n({(\underline{CA},\underline{A})}^{\overline{L}}) = 0$ for
$\pi_n({(\underline{CA},\underline{A})}^{\overline{L}}) = 0$ for ![]() $n \lt k-1$, we have that
$n \lt k-1$, we have that ![]() $\pi_n(H)=0$ for
$\pi_n(H)=0$ for ![]() $n \lt k-1$. When
$n \lt k-1$. When ![]() $n = k-1$, consider the following section of the long exact sequence
$n = k-1$, consider the following section of the long exact sequence
 \begin{equation*}\pi_{k}({(\underline{CA},\underline{A})}^K) \to \pi_{k-1}(H) \to \pi_{k-1}({(\underline{CA},\underline{A})}^{\overline{L}}) \to \pi_{k-1}({(\underline{CA},\underline{A})}^K).\end{equation*}
\begin{equation*}\pi_{k}({(\underline{CA},\underline{A})}^K) \to \pi_{k-1}(H) \to \pi_{k-1}({(\underline{CA},\underline{A})}^{\overline{L}}) \to \pi_{k-1}({(\underline{CA},\underline{A})}^K).\end{equation*} As  ${(\underline{CA},\underline{A})}^K$ is at least
${(\underline{CA},\underline{A})}^K$ is at least ![]() $(2k-2)$-connected by Lemma 2.15, this splits to give the isomorphism
$(2k-2)$-connected by Lemma 2.15, this splits to give the isomorphism
 \begin{equation*}\pi_{k-1}(H) \cong \pi_{k-1}({(\underline{CA},\underline{A})}^{\overline{L}}).\end{equation*}
\begin{equation*}\pi_{k-1}(H) \cong \pi_{k-1}({(\underline{CA},\underline{A})}^{\overline{L}}).\end{equation*} Therefore, ![]() $\pi_{k-1}(H)$ is precisley as connected as
$\pi_{k-1}(H)$ is precisley as connected as  $ \pi_{k-1}({(\underline{CA},\underline{A})}^{\overline{L}})$. By Corollary 2.16,
$ \pi_{k-1}({(\underline{CA},\underline{A})}^{\overline{L}})$. By Corollary 2.16,  ${(\underline{CA},\underline{A})}^{\overline{L}}$ is at least
${(\underline{CA},\underline{A})}^{\overline{L}}$ is at least ![]() $(k-1)$-connected, and therefore
$(k-1)$-connected, and therefore ![]() $H$ is at least
$H$ is at least ![]() $(k-1)$-connected.
$(k-1)$-connected.
2.3. Cube Lemma
We conclude this section by stating the Cube Lemma, which will be used in later constructions.
Lemma 2.18. ([Reference Mather19, Theorem 25])
Suppose there is a diagram of spaces and maps

where the bottom face is a homotopy pushout and the four sides are obtained by pulling back with ![]() $H \to D$. Then the top face is a homotopy pushout.
$H \to D$. Then the top face is a homotopy pushout.
A common construction of such a cube is to start with a homotopy pushout, and map all four corners of this pushout into a space ![]() $Z$, and take the top face to be a diagram of the homotopy fibres of these maps. This is equivalent to the statement that all four sides are homotopy pullbacks, and so the diagram of homotopy fibres is a homotopy pushout.
$Z$, and take the top face to be a diagram of the homotopy fibres of these maps. This is equivalent to the statement that all four sides are homotopy pullbacks, and so the diagram of homotopy fibres is a homotopy pushout.
3. Polyhedral join products
In this section, we introduce the polyhedral join product and prove many fundamental combinatorial results. Recall that the polyhedral join product, as defined by [Reference Abramyan and Panov1] is
 \begin{equation*}(\underline{K},\underline{L})^{*M} = \bigcup_{\sigma \in M} (\underline{K},\underline{L})^{*\sigma}\end{equation*}
\begin{equation*}(\underline{K},\underline{L})^{*M} = \bigcup_{\sigma \in M} (\underline{K},\underline{L})^{*\sigma}\end{equation*} where each ![]() $(\underline{K},\underline{L})^{*\sigma}$ is defined as
$(\underline{K},\underline{L})^{*\sigma}$ is defined as
 \begin{equation*}(\underline{K},\underline{L})^{*\sigma} = \overset{m}{\underset{i=1} \ast} \; Y_i,\;\; Y_i = \begin{cases} K_i & i \in \sigma \\ L_i & \mathrm{otherwise}. \end{cases}\end{equation*}
\begin{equation*}(\underline{K},\underline{L})^{*\sigma} = \overset{m}{\underset{i=1} \ast} \; Y_i,\;\; Y_i = \begin{cases} K_i & i \in \sigma \\ L_i & \mathrm{otherwise}. \end{cases}\end{equation*}We now consider some examples of polyhedral join products on pairs of simplicial complexes.
Example 3.1. Let ![]() $K$ be a simplicial complex on the vertex set
$K$ be a simplicial complex on the vertex set ![]() $[m]$, and let
$[m]$, and let ![]() $K_1,\dots,K_m$ be simplicial complexes on the vertex sets
$K_1,\dots,K_m$ be simplicial complexes on the vertex sets ![]() $[k_1],\dots,[k_m]$, respectively.
$[k_1],\dots,[k_m]$, respectively.
(1) The substitution complex
 $K(K_1,\dots,K_m)$ as introduced in [Reference Abramyan and Panov1] is the polyhedral join product on the pairs
$K(K_1,\dots,K_m)$ as introduced in [Reference Abramyan and Panov1] is the polyhedral join product on the pairs  $(K_i,\emptyset)$.
$(K_i,\emptyset)$.(2) The composition complex
 $K \langle K_1 ,\dots, K_m \rangle$ as introduced in [Reference Ayzenberg4] is the polyhedral join product on the pairs
$K \langle K_1 ,\dots, K_m \rangle$ as introduced in [Reference Ayzenberg4] is the polyhedral join product on the pairs  $\{(\Delta^{m_i-1},K_i)\}_{i=1}^m$.
$\{(\Delta^{m_i-1},K_i)\}_{i=1}^m$.
We now prove some combinatorial properties of the polyhedral join product.
Lemma 3.2. Let ![]() $M$ be a simplicial complex on the vertex set
$M$ be a simplicial complex on the vertex set ![]() $[m]$, and let
$[m]$, and let ![]() $N$ be a subcomplex on the vertex set
$N$ be a subcomplex on the vertex set ![]() $[l]$ where
$[l]$ where ![]() $l \leq m$. Then
$l \leq m$. Then  ${(\underline{K},\underline{L})}^{*N}$ is a subcomplex of
${(\underline{K},\underline{L})}^{*N}$ is a subcomplex of  ${(\underline{K},\underline{L})}^{*M}$. Furthermore, if
${(\underline{K},\underline{L})}^{*M}$. Furthermore, if ![]() $N$ is a full subcomplex of
$N$ is a full subcomplex of ![]() $M$,
$M$,  ${(\underline{K},\underline{L})}^{*N}$ is a full subcomplex of
${(\underline{K},\underline{L})}^{*N}$ is a full subcomplex of  ${(\underline{K},\underline{L})}^{*M}$.
${(\underline{K},\underline{L})}^{*M}$.
Proof. Let ![]() $\tau_i$ denote a simplex in
$\tau_i$ denote a simplex in ![]() $K_i$ and let
$K_i$ and let ![]() $\omega_i$ denote a simplex in
$\omega_i$ denote a simplex in ![]() $L_i$. Every simplex
$L_i$. Every simplex ![]() $\sigma \in N$ will generate simplices of the form
$\sigma \in N$ will generate simplices of the form ![]() $(\cup_{i \in \sigma} \tau_i) \cup (\cup_{i \notin \sigma} \omega_i)$. As
$(\cup_{i \in \sigma} \tau_i) \cup (\cup_{i \notin \sigma} \omega_i)$. As ![]() $N$ is a subcomplex of
$N$ is a subcomplex of ![]() $M$,
$M$, ![]() $\sigma \in M$, and so
$\sigma \in M$, and so  $(\cup_{i \in \sigma} \tau_i) \cup (\cup_{i \notin \sigma} \omega_i) \in {(\underline{K},\underline{L})}^{*M}$ for all
$(\cup_{i \in \sigma} \tau_i) \cup (\cup_{i \notin \sigma} \omega_i) \in {(\underline{K},\underline{L})}^{*M}$ for all ![]() $\sigma \in N$. Therefore,
$\sigma \in N$. Therefore,  ${(\underline{K},\underline{L})}^{*N}$ is a subcomplex of
${(\underline{K},\underline{L})}^{*N}$ is a subcomplex of  ${(\underline{K},\underline{L})}^{*M}$. Now let
${(\underline{K},\underline{L})}^{*M}$. Now let ![]() $N$ be a full subcomplex of
$N$ be a full subcomplex of ![]() $M$. Assume
$M$. Assume  ${(\underline{K},\underline{L})}^{*N}$ is not a full subcomplex of
${(\underline{K},\underline{L})}^{*N}$ is not a full subcomplex of ![]() $M$, that is, there exists a simplex
$M$, that is, there exists a simplex ![]() $\sigma'$ on the vertex set of
$\sigma'$ on the vertex set of  ${(\underline{K},\underline{L})}^{*N}$ such that
${(\underline{K},\underline{L})}^{*N}$ such that  $\sigma' \in {(\underline{K},\underline{L})}^{*M}$, but
$\sigma' \in {(\underline{K},\underline{L})}^{*M}$, but  $\sigma' \notin {(\underline{K},\underline{L})}^{*N}$. By definition,
$\sigma' \notin {(\underline{K},\underline{L})}^{*N}$. By definition, ![]() $\sigma' = (\cup_{i \in \sigma} \tau_i) \cup (\cup_{i \notin \sigma} \omega_i)$ for some
$\sigma' = (\cup_{i \in \sigma} \tau_i) \cup (\cup_{i \notin \sigma} \omega_i)$ for some ![]() $\sigma \in M$. As
$\sigma \in M$. As ![]() $N$ is a full subcomplex of
$N$ is a full subcomplex of ![]() $M$,
$M$, ![]() $\sigma \in N$. By the definition of the polyhedral join product,
$\sigma \in N$. By the definition of the polyhedral join product, ![]() $(\cup_{i \in \sigma} \tau_i) \cup (\cup_{i \notin \sigma} \omega_i)$ will form a simplex in
$(\cup_{i \in \sigma} \tau_i) \cup (\cup_{i \notin \sigma} \omega_i)$ will form a simplex in  ${(\underline{K},\underline{L})}^{*N}$, contradicting the claim that
${(\underline{K},\underline{L})}^{*N}$, contradicting the claim that  $\sigma' \notin {(\underline{K},\underline{L})}^{*N}$. Therefore,
$\sigma' \notin {(\underline{K},\underline{L})}^{*N}$. Therefore,  ${(\underline{K},\underline{L})}^{*N}$ is a full subcomplex of
${(\underline{K},\underline{L})}^{*N}$ is a full subcomplex of  ${(\underline{K},\underline{L})}^{*M}$.
${(\underline{K},\underline{L})}^{*M}$.
Lemma 3.3. Let

be a pushout of simplicial complexes. Then

is a pushout of simplicial complexes, where ![]() $M$ is on the vertex set
$M$ is on the vertex set ![]() $[m]$, and
$[m]$, and ![]() $\overline{N}$,
$\overline{N}$, ![]() $\overline{M_A}$ and
$\overline{M_A}$ and ![]() $\overline{M_B}$ refer to
$\overline{M_B}$ refer to ![]() $N$,
$N$,![]() $M_A$,
$M_A$,![]() $M_B$ regarded as simplicial complexes on the vertex set of
$M_B$ regarded as simplicial complexes on the vertex set of ![]() $M$.
$M$.
Proof. As ![]() $M$ is finite, the faces in
$M$ is finite, the faces in ![]() $M$ can be sorted into three categories: (X) the faces in
$M$ can be sorted into three categories: (X) the faces in ![]() $N$, (Y) the faces in
$N$, (Y) the faces in ![]() $M_A$ that are not in
$M_A$ that are not in ![]() $N$ and (Z) the faces in
$N$ and (Z) the faces in ![]() $M_B$ that are not in
$M_B$ that are not in ![]() $N$. Therefore, we have that
$N$. Therefore, we have that
 \begin{equation*}N = \bigcup_{\sigma \in X} \sigma,\end{equation*}
\begin{equation*}N = \bigcup_{\sigma \in X} \sigma,\end{equation*} \begin{equation*}M_A = \big(\bigcup_{\sigma \in X} \sigma \big) \cup \big(\bigcup_{\sigma' \in Y} \sigma'\big),\end{equation*}
\begin{equation*}M_A = \big(\bigcup_{\sigma \in X} \sigma \big) \cup \big(\bigcup_{\sigma' \in Y} \sigma'\big),\end{equation*} \begin{equation*}M_B = \big(\bigcup_{\sigma \in X} \sigma \big) \cup \big(\bigcup_{\sigma'' \in Z} \sigma''\big),\end{equation*}
\begin{equation*}M_B = \big(\bigcup_{\sigma \in X} \sigma \big) \cup \big(\bigcup_{\sigma'' \in Z} \sigma''\big),\end{equation*} \begin{equation*}M = \big(\bigcup_{\sigma \in X} \sigma \big) \cup \big(\bigcup_{\sigma' \in Y} \sigma'\big) \cup \big(\bigcup_{\sigma'' \in Z} \sigma''\big).\end{equation*}
\begin{equation*}M = \big(\bigcup_{\sigma \in X} \sigma \big) \cup \big(\bigcup_{\sigma' \in Y} \sigma'\big) \cup \big(\bigcup_{\sigma'' \in Z} \sigma''\big).\end{equation*} By the definition of the polyhedral join product, we have that  ${(\underline{K},\underline{L})}^{*M} = \bigcup_{\sigma \in M} {(\underline{K},\underline{L})}^{*\sigma}$. Therefore,
${(\underline{K},\underline{L})}^{*M} = \bigcup_{\sigma \in M} {(\underline{K},\underline{L})}^{*\sigma}$. Therefore,
 \begin{equation*}{(\underline{K},\underline{L})}^{*\overline{N}} = \bigcup_{\sigma \in X} {(\underline{K},\underline{L})}^{*\sigma},\end{equation*}
\begin{equation*}{(\underline{K},\underline{L})}^{*\overline{N}} = \bigcup_{\sigma \in X} {(\underline{K},\underline{L})}^{*\sigma},\end{equation*} \begin{equation*}{(\underline{K},\underline{L})}^{*\overline{M_A}} = \big(\bigcup_{\sigma \in X} {(\underline{K},\underline{L})}^{*\sigma} \big) \cup \big(\bigcup_{\sigma' \in Y} {(\underline{K},\underline{L})}^{*\sigma'}\big),\end{equation*}
\begin{equation*}{(\underline{K},\underline{L})}^{*\overline{M_A}} = \big(\bigcup_{\sigma \in X} {(\underline{K},\underline{L})}^{*\sigma} \big) \cup \big(\bigcup_{\sigma' \in Y} {(\underline{K},\underline{L})}^{*\sigma'}\big),\end{equation*} \begin{equation*} {(\underline{K},\underline{L})}^{*\overline{M_B}}= \big(\bigcup_{\sigma \in X} {(\underline{K},\underline{L})}^{*\sigma} \big) \cup \big(\bigcup_{\sigma'' \in Z} {(\underline{K},\underline{L})}^{*\sigma''} \big),\end{equation*}
\begin{equation*} {(\underline{K},\underline{L})}^{*\overline{M_B}}= \big(\bigcup_{\sigma \in X} {(\underline{K},\underline{L})}^{*\sigma} \big) \cup \big(\bigcup_{\sigma'' \in Z} {(\underline{K},\underline{L})}^{*\sigma''} \big),\end{equation*} \begin{equation*}{(\underline{K},\underline{L})}^{*M} = \big(\bigcup_{\sigma \in X} {(\underline{K},\underline{L})}^{*\sigma} \big) \cup \big(\bigcup_{\sigma' \in Y} {(\underline{K},\underline{L})}^{*\sigma'}\big) \cup \big(\bigcup_{\sigma'' \in Z} {(\underline{K},\underline{L})}^{*\sigma''}\big).\end{equation*}
\begin{equation*}{(\underline{K},\underline{L})}^{*M} = \big(\bigcup_{\sigma \in X} {(\underline{K},\underline{L})}^{*\sigma} \big) \cup \big(\bigcup_{\sigma' \in Y} {(\underline{K},\underline{L})}^{*\sigma'}\big) \cup \big(\bigcup_{\sigma'' \in Z} {(\underline{K},\underline{L})}^{*\sigma''}\big).\end{equation*} As  ${(\underline{K},\underline{L})}^{*\overline{M_A}} \cup {(\underline{K},\underline{L})}^{*\overline{M_B}} = {(\underline{K},\underline{L})}^{*M}$ and
${(\underline{K},\underline{L})}^{*\overline{M_A}} \cup {(\underline{K},\underline{L})}^{*\overline{M_B}} = {(\underline{K},\underline{L})}^{*M}$ and  ${(\underline{K},\underline{L})}^{*\overline{M_A}} \cap {(\underline{K},\underline{L})}^{*\overline{M_B}} = {(\underline{K},\underline{L})}^{*\overline{N}}$, the result holds.
${(\underline{K},\underline{L})}^{*\overline{M_A}} \cap {(\underline{K},\underline{L})}^{*\overline{M_B}} = {(\underline{K},\underline{L})}^{*\overline{N}}$, the result holds.
Lemma 3.4. There is an equality of simplicial complexes
 \begin{equation*}{(\underline{K},\underline{L})}^{*(M*N)} = {(\underline{K},\underline{L})}^{*M}*{(\underline{K},\underline{L})}^{*N}.\end{equation*}
\begin{equation*}{(\underline{K},\underline{L})}^{*(M*N)} = {(\underline{K},\underline{L})}^{*M}*{(\underline{K},\underline{L})}^{*N}.\end{equation*}Proof. Simplices in ![]() $M*N$ will be of the form
$M*N$ will be of the form ![]() $\sigma \cup \tau$, where
$\sigma \cup \tau$, where ![]() $\sigma \in M$,
$\sigma \in M$, ![]() $ \tau \in N$. Consider
$ \tau \in N$. Consider  ${(\underline{K},\underline{L})}^{*\sigma \cup \tau}$. By definition, this is
${(\underline{K},\underline{L})}^{*\sigma \cup \tau}$. By definition, this is ![]() $*^{m}_{i=1} Y_i$ where
$*^{m}_{i=1} Y_i$ where ![]() $Y_i = K_i$ if
$Y_i = K_i$ if ![]() $i \in \sigma \cup \tau$ and
$i \in \sigma \cup \tau$ and ![]() $L_i$ otherwise. As
$L_i$ otherwise. As ![]() $\sigma$ and
$\sigma$ and ![]() $\tau$ are on disjoint vertex sets,
$\tau$ are on disjoint vertex sets, ![]() $*^{m}_{i=1} Y_i$ can be written as
$*^{m}_{i=1} Y_i$ can be written as  $(*_{j=1}^{l} Y_i) * (*_{k=l+1}^m Y_k)$ where
$(*_{j=1}^{l} Y_i) * (*_{k=l+1}^m Y_k)$ where ![]() $Y_j = K_j$ if
$Y_j = K_j$ if ![]() $j \in \sigma$ and
$j \in \sigma$ and ![]() $L_j$ otherwise, and
$L_j$ otherwise, and ![]() $Y_k=K_k$ if
$Y_k=K_k$ if ![]() $k \in \tau$, and
$k \in \tau$, and ![]() $L_k$ otherwise. Therefore,
$L_k$ otherwise. Therefore, ![]() ${(\underline{K},\underline{L})}^{*\sigma \cup \tau} = {(\underline{K},\underline{L})}^{*\sigma} * {(\underline{K},\underline{L})}^{*\tau}$. Now
${(\underline{K},\underline{L})}^{*\sigma \cup \tau} = {(\underline{K},\underline{L})}^{*\sigma} * {(\underline{K},\underline{L})}^{*\tau}$. Now
 \begin{multline*}{(\underline{K},\underline{L})}^{*(M*N)}= \bigcup_{\sigma \in M, \tau \in N} {(\underline{K},\underline{L})}^{*\sigma \cup \tau} = \bigcup_{\sigma \in M, \tau \in N} {(\underline{K},\underline{L})}^{*\sigma} * {(\underline{K},\underline{L})}^{*\tau} = \\ \big( \bigcup_{\sigma \in M} {(\underline{K},\underline{L})}^{*\sigma} \big) * \big( \bigcup_{\tau \in N} {(\underline{K},\underline{L})}^{*\tau} \big) = {(\underline{K},\underline{L})}^{*M} * {(\underline{K},\underline{L})}^{*N}. \end{multline*}
\begin{multline*}{(\underline{K},\underline{L})}^{*(M*N)}= \bigcup_{\sigma \in M, \tau \in N} {(\underline{K},\underline{L})}^{*\sigma \cup \tau} = \bigcup_{\sigma \in M, \tau \in N} {(\underline{K},\underline{L})}^{*\sigma} * {(\underline{K},\underline{L})}^{*\tau} = \\ \big( \bigcup_{\sigma \in M} {(\underline{K},\underline{L})}^{*\sigma} \big) * \big( \bigcup_{\tau \in N} {(\underline{K},\underline{L})}^{*\tau} \big) = {(\underline{K},\underline{L})}^{*M} * {(\underline{K},\underline{L})}^{*N}. \end{multline*}Lemma 3.5. Let ![]() $N$ be a simplicial complex on the vertex set
$N$ be a simplicial complex on the vertex set ![]() $[m-1]$, and let
$[m-1]$, and let ![]() $\overline{N}$ be the simplicial complex
$\overline{N}$ be the simplicial complex ![]() $N$ considered as a simplicial complex on
$N$ considered as a simplicial complex on ![]() $[m]$. Then
$[m]$. Then  ${(\underline{K},\underline{L})}^{*\overline{N}} = {(\underline{K},\underline{L})}^{*N} * L_m$.
${(\underline{K},\underline{L})}^{*\overline{N}} = {(\underline{K},\underline{L})}^{*N} * L_m$.
Proof. Let ![]() $\sigma$ denote a simplex in
$\sigma$ denote a simplex in ![]() $N$, and let
$N$, and let ![]() $\overline{\sigma}$ denote the same simplex viewed as a simplex in
$\overline{\sigma}$ denote the same simplex viewed as a simplex in ![]() $\overline{N}$. Consider
$\overline{N}$. Consider  ${(\underline{K},\underline{L})}^{*\overline{\sigma}}$. By definition, this is
${(\underline{K},\underline{L})}^{*\overline{\sigma}}$. By definition, this is  $\overset{m}{\underset{i=1}{\ast}} \; Y_i = (\underset{i \in \overline{\sigma}}{\ast} K_i) \ast (\underset{i \notin \overline{\sigma}}{\ast} L_i)$. As
$\overset{m}{\underset{i=1}{\ast}} \; Y_i = (\underset{i \in \overline{\sigma}}{\ast} K_i) \ast (\underset{i \notin \overline{\sigma}}{\ast} L_i)$. As ![]() $m$ is a ghost vertex,
$m$ is a ghost vertex, ![]() $m \notin \overline{\sigma}$ for all
$m \notin \overline{\sigma}$ for all ![]() $\overline{\sigma} \in \overline{N}$, and so
$\overline{\sigma} \in \overline{N}$, and so
 \begin{equation*}{(\underline{K},\underline{L})}^{*\overline{\sigma}} = (\underset{i \in \sigma}{\ast} K_i )* (\underset{i \notin \sigma, i \neq m}{\ast} L_i) * L_m = {(\underline{K},\underline{L})}^{*\sigma} * L_m\end{equation*}
\begin{equation*}{(\underline{K},\underline{L})}^{*\overline{\sigma}} = (\underset{i \in \sigma}{\ast} K_i )* (\underset{i \notin \sigma, i \neq m}{\ast} L_i) * L_m = {(\underline{K},\underline{L})}^{*\sigma} * L_m\end{equation*} where ![]() $\sigma$ is now considered a simplex of
$\sigma$ is now considered a simplex of ![]() $N$. Taking the union over all faces
$N$. Taking the union over all faces ![]() $\sigma \in N$ gives the required result.
$\sigma \in N$ gives the required result.
Corollary 3.6. There is a pushout

where ![]() $\mathrm{lk}_M(i)$ is regarded as a simplicial complex on the vertex set of
$\mathrm{lk}_M(i)$ is regarded as a simplicial complex on the vertex set of ![]() $M \setminus i$.
$M \setminus i$.
We can construct the polyhedral join product sequentially as follows. Define ![]() $M(i)$ as the polyhedral join product
$M(i)$ as the polyhedral join product  $(\underline{P^i},\underline{Q^i})^{*M}$ where the sequence
$(\underline{P^i},\underline{Q^i})^{*M}$ where the sequence  $(\underline{P^i},\underline{Q^i})$ is defined as
$(\underline{P^i},\underline{Q^i})$ is defined as
 \begin{equation*}(P^i_j,Q^i_j) = \begin{cases} (K_j,L_j) & j \leq i\\ (\{j\},\emptyset) & j \gt i. \end{cases}\end{equation*}
\begin{equation*}(P^i_j,Q^i_j) = \begin{cases} (K_j,L_j) & j \leq i\\ (\{j\},\emptyset) & j \gt i. \end{cases}\end{equation*} The vertex set of ![]() $M(i)$ shall be regarded as
$M(i)$ shall be regarded as
 \begin{equation*}\{\{j^1_{1},\dots,j^1_{k_1}\},\{j^2_{1},\dots,j^2_{k_2}\},\dots,\{j^i_{1},\dots,j^i_{k_i}\},i+1,\dots,m\}=\{[k_1],\dots,[k_i],i+1,\dots,m\}\end{equation*}
\begin{equation*}\{\{j^1_{1},\dots,j^1_{k_1}\},\{j^2_{1},\dots,j^2_{k_2}\},\dots,\{j^i_{1},\dots,j^i_{k_i}\},i+1,\dots,m\}=\{[k_1],\dots,[k_i],i+1,\dots,m\}\end{equation*} This allows us to keep track of the original vertex set of ![]() $M$ and the new vertices added by the polyhedral join operation.
$M$ and the new vertices added by the polyhedral join operation.
Note that  $M(m) = {(\underline{K},\underline{L})}^{*M}$,
$M(m) = {(\underline{K},\underline{L})}^{*M}$, ![]() $M(0) = M$, and each
$M(0) = M$, and each ![]() $M(i)$ is a subcomplex of
$M(i)$ is a subcomplex of ![]() $M(i+1)$.
$M(i+1)$.
Lemma 3.7. Let ![]() ${(\underline{K},\underline{L})}$ be a sequence of pairs of simplicial complexes, and let
${(\underline{K},\underline{L})}$ be a sequence of pairs of simplicial complexes, and let ![]() $(\underline{P},\underline{Q})$ be a sequence of simplicial complexes such that
$(\underline{P},\underline{Q})$ be a sequence of simplicial complexes such that
 \begin{equation*}(P_j,Q_j) = \begin{cases} (K_j,L_j) & j \neq i \\ (\{i\},\emptyset) & j = i. \end{cases}\end{equation*}
\begin{equation*}(P_j,Q_j) = \begin{cases} (K_j,L_j) & j \neq i \\ (\{i\},\emptyset) & j = i. \end{cases}\end{equation*}Then there is an identity of simplical complexes
 \begin{equation*}{(\underline{K},\underline{L})}^{*M\setminus i} = ((\underline{P},\underline{Q})^{*M}) \setminus i.\end{equation*}
\begin{equation*}{(\underline{K},\underline{L})}^{*M\setminus i} = ((\underline{P},\underline{Q})^{*M}) \setminus i.\end{equation*}Furthermore, there is an identity of simplical complexes
 \begin{equation*}{(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)} = \mathrm{lk}_{(\underline{P},\underline{Q})^{*M}} (i)\end{equation*}
\begin{equation*}{(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)} = \mathrm{lk}_{(\underline{P},\underline{Q})^{*M}} (i)\end{equation*} where ![]() $\mathrm{lk}_M(i)$ is considered on the vertex set of
$\mathrm{lk}_M(i)$ is considered on the vertex set of ![]() $M \setminus i$ and
$M \setminus i$ and  $\mathrm{lk}_{(\underline{P},\underline{Q})^{*M}} (i)$ is considered on the vertex set of
$\mathrm{lk}_{(\underline{P},\underline{Q})^{*M}} (i)$ is considered on the vertex set of  $((\underline{P},\underline{Q})^{*M}) \setminus i$.
$((\underline{P},\underline{Q})^{*M}) \setminus i$.
Proof. Let ![]() $\tau_j$ denote a simplex in
$\tau_j$ denote a simplex in ![]() $K_j$ and let
$K_j$ and let ![]() $\omega_j$ denote a simplex in
$\omega_j$ denote a simplex in ![]() $L_j$. The simplices of
$L_j$. The simplices of  ${(\underline{K},\underline{L})}^{*M\setminus i}$ are all of the form
${(\underline{K},\underline{L})}^{*M\setminus i}$ are all of the form ![]() $( \cup_{j \in \sigma} \tau_j ) \cup ( \cup_{j \notin \sigma, j \neq i} \omega_j)$ for
$( \cup_{j \in \sigma} \tau_j ) \cup ( \cup_{j \notin \sigma, j \neq i} \omega_j)$ for ![]() $\sigma \in M \setminus i$. As every simplex of
$\sigma \in M \setminus i$. As every simplex of ![]() $M \setminus i$ is a simplex of
$M \setminus i$ is a simplex of ![]() $M$, all such simplices will be contained in
$M$, all such simplices will be contained in  $((\underline{P},\underline{Q})^{*M})$. As
$((\underline{P},\underline{Q})^{*M})$. As ![]() $ i \notin \sigma$, these simplices will be unchanged under the deletion of
$ i \notin \sigma$, these simplices will be unchanged under the deletion of ![]() $i$ from
$i$ from  $((\underline{P},\underline{Q})^{*M})$. Therefore,
$((\underline{P},\underline{Q})^{*M})$. Therefore,  ${(\underline{K},\underline{L})}^{*M\setminus i} \subseteq ((\underline{P},\underline{Q})^{*M}) \setminus i$. The simplices of
${(\underline{K},\underline{L})}^{*M\setminus i} \subseteq ((\underline{P},\underline{Q})^{*M}) \setminus i$. The simplices of  $((\underline{P},\underline{Q})^{*M}) \setminus i$ will be of two forms: those induced by
$((\underline{P},\underline{Q})^{*M}) \setminus i$ will be of two forms: those induced by ![]() $\gamma \in M$, such that
$\gamma \in M$, such that ![]() $i \notin \gamma$, and those induced by
$i \notin \gamma$, and those induced by ![]() $\kappa \in M$ such that
$\kappa \in M$ such that ![]() $i \in \kappa$. The simplices of
$i \in \kappa$. The simplices of  $((\underline{P},\underline{Q})^{*M}) \setminus i$ induced by
$((\underline{P},\underline{Q})^{*M}) \setminus i$ induced by ![]() $\gamma$ are clearly in
$\gamma$ are clearly in  ${(\underline{K},\underline{L})}^{*M\setminus i}$. If
${(\underline{K},\underline{L})}^{*M\setminus i}$. If ![]() $\kappa \in M$ contains
$\kappa \in M$ contains ![]() $i$, then
$i$, then ![]() $\kappa$ generates simplices of the form
$\kappa$ generates simplices of the form  $(( \cup_{j \in \kappa} \tau_j ) \cup ( \cup_{j\notin \kappa} \omega_j)) \setminus i = (( \cup_{j \in \kappa,j \neq i} \tau_j ) \cup ( \cup_{j \notin \kappa, j \neq i} \omega_j) \cup \{i\}) \setminus \{i\} = ( \cup_{j\ \in \kappa,j \neq i} \tau_j ) \cup ( \cup_{j \notin \kappa} \omega_j)$. As
$(( \cup_{j \in \kappa} \tau_j ) \cup ( \cup_{j\notin \kappa} \omega_j)) \setminus i = (( \cup_{j \in \kappa,j \neq i} \tau_j ) \cup ( \cup_{j \notin \kappa, j \neq i} \omega_j) \cup \{i\}) \setminus \{i\} = ( \cup_{j\ \in \kappa,j \neq i} \tau_j ) \cup ( \cup_{j \notin \kappa} \omega_j)$. As ![]() $\kappa \in M$ and
$\kappa \in M$ and ![]() $i \in \kappa$, we have
$i \in \kappa$, we have ![]() $\kappa \setminus i \in M \setminus i$. Therefore,
$\kappa \setminus i \in M \setminus i$. Therefore,  ${(\underline{K},\underline{L})}^{*M \setminus i}$ contains all simplices of the form
${(\underline{K},\underline{L})}^{*M \setminus i}$ contains all simplices of the form ![]() $( \cup_{j \in \kappa, j\neq i} \tau_j ) \cup ( \cup_{j \notin \kappa} \omega_j)$. As all simplices of
$( \cup_{j \in \kappa, j\neq i} \tau_j ) \cup ( \cup_{j \notin \kappa} \omega_j)$. As all simplices of  $((\underline{P},\underline{Q})^{*M}) \setminus i$ are contained in
$((\underline{P},\underline{Q})^{*M}) \setminus i$ are contained in  ${(\underline{K},\underline{L})}^{*M \setminus i}$, we obtain
${(\underline{K},\underline{L})}^{*M \setminus i}$, we obtain  $((\underline{P},\underline{Q})^{*M})\setminus i \subseteq {(\underline{K},\underline{L})}^{*M \setminus i}$. We therefore have
$((\underline{P},\underline{Q})^{*M})\setminus i \subseteq {(\underline{K},\underline{L})}^{*M \setminus i}$. We therefore have  ${(\underline{K},\underline{L})}^{*M \setminus i} = ((\underline{P},\underline{Q})^{*M}) \setminus i$.
${(\underline{K},\underline{L})}^{*M \setminus i} = ((\underline{P},\underline{Q})^{*M}) \setminus i$.
Now, let us consider the second statement. Simplices of  ${(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)}$ are of the form
${(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)}$ are of the form ![]() $(\cup_{j \in \sigma} \tau_j) \cup (\cup_{j \notin \sigma} \omega_j)$ where
$(\cup_{j \in \sigma} \tau_j) \cup (\cup_{j \notin \sigma} \omega_j)$ where ![]() $\omega \cup i \in M$. By Lemma 3.2,
$\omega \cup i \in M$. By Lemma 3.2,  ${(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)}$ is a subcomplex of
${(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)}$ is a subcomplex of  ${(\underline{K},\underline{L})}^{*M\setminus i}$, and so by the above equality,
${(\underline{K},\underline{L})}^{*M\setminus i}$, and so by the above equality,  ${(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)}$ is a subcomplex of
${(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)}$ is a subcomplex of  $(\underline{P},\underline{Q})^{*M} \setminus i$, and so
$(\underline{P},\underline{Q})^{*M} \setminus i$, and so ![]() $(\cup_{j \in \sigma} \tau_j) \cup (\cup_{j \notin \sigma} \omega_j)$ is contained in
$(\cup_{j \in \sigma} \tau_j) \cup (\cup_{j \notin \sigma} \omega_j)$ is contained in  $(\underline{P},\underline{Q})^{*M} \setminus i$. As
$(\underline{P},\underline{Q})^{*M} \setminus i$. As ![]() $\sigma \in \mathrm{lk}_M(i)$,
$\sigma \in \mathrm{lk}_M(i)$, ![]() $\sigma \cup i \in M$, and therefore
$\sigma \cup i \in M$, and therefore ![]() $(\cup_{j \in \sigma }\tau_j) \cup (\cup_{j\notin \sigma, j \neq i} \omega_j) \cup i$ is a simplex of
$(\cup_{j \in \sigma }\tau_j) \cup (\cup_{j\notin \sigma, j \neq i} \omega_j) \cup i$ is a simplex of  $(\underline{P},\underline{Q})^{*M}$. By the definition of the link of a vertex, the simplex
$(\underline{P},\underline{Q})^{*M}$. By the definition of the link of a vertex, the simplex ![]() $(\cup_{j \in \sigma} \tau_j) \cup (\cup_{j \notin \sigma, j \neq i} \omega_j)$ is contained in
$(\cup_{j \in \sigma} \tau_j) \cup (\cup_{j \notin \sigma, j \neq i} \omega_j)$ is contained in  $\mathrm{lk}_{(\underline{P},\underline{Q})^{*M})}(i)$. Therefore,
$\mathrm{lk}_{(\underline{P},\underline{Q})^{*M})}(i)$. Therefore,  ${(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)} \subseteq \mathrm{lk}_{(\underline{P},\underline{Q})^{*M})}(i)$. Now consider a simplex in
${(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)} \subseteq \mathrm{lk}_{(\underline{P},\underline{Q})^{*M})}(i)$. Now consider a simplex in  $\mathrm{lk}_{(\underline{P},\underline{Q})^{*M}}(i)$. Such simplices have the form
$\mathrm{lk}_{(\underline{P},\underline{Q})^{*M}}(i)$. Such simplices have the form ![]() $(\cup_{j \in \gamma} \tau_j) \cup (\cup_{j \notin \gamma, j \neq i} \omega_j)$ where
$(\cup_{j \in \gamma} \tau_j) \cup (\cup_{j \notin \gamma, j \neq i} \omega_j)$ where  $(\cup_{j \in \gamma} \tau_j) \cup (\cup_{j \notin \gamma, j \neq i} \omega_j) \cup i \in (\underline{P},\underline{Q})^{*M}$. As
$(\cup_{j \in \gamma} \tau_j) \cup (\cup_{j \notin \gamma, j \neq i} \omega_j) \cup i \in (\underline{P},\underline{Q})^{*M}$. As ![]() $(\cup_{j \in \gamma} \tau_j) \cup (\cup_{j \notin \gamma, j \neq i} \omega_j) \cup \{i\}$ is a simplex of
$(\cup_{j \in \gamma} \tau_j) \cup (\cup_{j \notin \gamma, j \neq i} \omega_j) \cup \{i\}$ is a simplex of  $(\underline{P},\underline{Q})^{*M}$, this implies that
$(\underline{P},\underline{Q})^{*M}$, this implies that ![]() $\gamma \cup \{i\}$ is a simplex of
$\gamma \cup \{i\}$ is a simplex of ![]() $M$. Therefore, for all
$M$. Therefore, for all ![]() $\gamma$ such that
$\gamma$ such that  $(\cup_{j \in \gamma} \tau_j) \cup (\cup_{j \notin \gamma, j \neq i} \omega_j) \in \mathrm{lk}_{(\underline{P},\underline{Q})^{*M}}(i)$, the simplex
$(\cup_{j \in \gamma} \tau_j) \cup (\cup_{j \notin \gamma, j \neq i} \omega_j) \in \mathrm{lk}_{(\underline{P},\underline{Q})^{*M}}(i)$, the simplex ![]() $\gamma \in \mathrm{lk}_M(i)$. Therefore,
$\gamma \in \mathrm{lk}_M(i)$. Therefore,  $(\cup_{j \in \gamma} \tau_j) \cup (\cup_{j \notin \gamma, j \neq m} \omega_j) \in {(\underline{K},\underline{L})}^{*\mathrm{lk}_M(j)}$, and so
$(\cup_{j \in \gamma} \tau_j) \cup (\cup_{j \notin \gamma, j \neq m} \omega_j) \in {(\underline{K},\underline{L})}^{*\mathrm{lk}_M(j)}$, and so  $\mathrm{lk}_{(\underline{P},\underline{Q})^{*M}}(i) \subseteq {(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)}$. We therefore have the equality
$\mathrm{lk}_{(\underline{P},\underline{Q})^{*M}}(i) \subseteq {(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)}$. We therefore have the equality  ${(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)} = \mathrm{lk}_{(\underline{P},\underline{Q})^{*M}}(i)$.
${(\underline{K},\underline{L})}^{*\mathrm{lk}_M(i)} = \mathrm{lk}_{(\underline{P},\underline{Q})^{*M}}(i)$.
Lemma 3.8. Let ![]() ${(\underline{K},\underline{L})}$ be a sequence of pairs of simplicial complexes, and let
${(\underline{K},\underline{L})}$ be a sequence of pairs of simplicial complexes, and let ![]() $(\underline{P},\underline{Q})$ be a sequence of simplicial complexes such that
$(\underline{P},\underline{Q})$ be a sequence of simplicial complexes such that
 \begin{equation*}(P_j,Q_j) = \begin{cases} (K_j,L_j) & j \neq i \\ (\{i\},\emptyset) & j = i. \end{cases}\end{equation*}
\begin{equation*}(P_j,Q_j) = \begin{cases} (K_j,L_j) & j \neq i \\ (\{i\},\emptyset) & j = i. \end{cases}\end{equation*} Let  $\overline{(\underline{P},\underline{Q})^{*M}}$ be the simplicial complex defined by the pushout
$\overline{(\underline{P},\underline{Q})^{*M}}$ be the simplicial complex defined by the pushout

Then there is an identity of simplicial complexes
 \begin{equation*}{(\underline{K},\underline{L})}^{*M} = \overline{(\underline{P},\underline{Q})^{*M}}\end{equation*}
\begin{equation*}{(\underline{K},\underline{L})}^{*M} = \overline{(\underline{P},\underline{Q})^{*M}}\end{equation*}Proof. By Lemma 3.7 we can rewrite  $(\underline{P},\underline{Q})^{*M} \setminus i$ and
$(\underline{P},\underline{Q})^{*M} \setminus i$ and 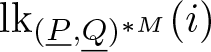 $\mathrm{lk}_{(\underline{P},\underline{Q})^{*M}}(i)$. Therefore, the pushout defining
$\mathrm{lk}_{(\underline{P},\underline{Q})^{*M}}(i)$. Therefore, the pushout defining  $ \overline{(\underline{P},\underline{Q})^{*M}}$ can be written as
$ \overline{(\underline{P},\underline{Q})^{*M}}$ can be written as

By Lemma 3.6,  $\overline{(\underline{P},\underline{Q})^{*M}} = {(\underline{K},\underline{L})}^{*M}$.
$\overline{(\underline{P},\underline{Q})^{*M}} = {(\underline{K},\underline{L})}^{*M}$.
Recall that ![]() $M(i)$ is defined as polyhedral join product
$M(i)$ is defined as polyhedral join product  $(\underline{P^i},\underline{Q^i})^{*M}$ where the sequence
$(\underline{P^i},\underline{Q^i})^{*M}$ where the sequence  $(\underline{P^i},\underline{Q^i})$ is defined as
$(\underline{P^i},\underline{Q^i})$ is defined as
 \begin{equation*}(P^i_j,Q^i_j) = \begin{cases} (K_j,L_j) & j \leq i\\ (\{j\},\emptyset) & j \gt i. \end{cases}\end{equation*}
\begin{equation*}(P^i_j,Q^i_j) = \begin{cases} (K_j,L_j) & j \leq i\\ (\{j\},\emptyset) & j \gt i. \end{cases}\end{equation*} By Lemma 3.8, with  ${(\underline{K},\underline{L})} = (\underline{P^{i+1}},\underline{Q^{i+1}})$ and
${(\underline{K},\underline{L})} = (\underline{P^{i+1}},\underline{Q^{i+1}})$ and  $(\underline{P},\underline{Q})= (\underline{P^i},\underline{Q^i})$, we obtain
$(\underline{P},\underline{Q})= (\underline{P^i},\underline{Q^i})$, we obtain ![]() $M(i+1)$ from
$M(i+1)$ from ![]() $M(i)$ via the pushout
$M(i)$ via the pushout

We, therefore, obtain the following result.
Lemma 3.9. The polyhedral join product can be constructed sequentially. That is, given a simplicial complex ![]() $M$ on the vertex set
$M$ on the vertex set ![]() $[m]$, we can obtain
$[m]$, we can obtain  ${(\underline{K},\underline{L})}^{*M}$ via the following sequence
${(\underline{K},\underline{L})}^{*M}$ via the following sequence
 \begin{equation*}M \subset M(1) \subset M(2) \subset \dots \subset M(m) = {(\underline{K},\underline{L})}^{*M}\end{equation*}
\begin{equation*}M \subset M(1) \subset M(2) \subset \dots \subset M(m) = {(\underline{K},\underline{L})}^{*M}\end{equation*} where at each point, ![]() $M(i+1)$ is obtained from
$M(i+1)$ is obtained from ![]() $M(i)$ via the pushout
$M(i)$ via the pushout

Specialising in the substitution complex, we give specific results concerning full subcomplexes.
Lemma 3.10. Let ![]() $K$ be a simplicial complex on
$K$ be a simplicial complex on ![]() $[m]$ vertices, and let
$[m]$ vertices, and let ![]() $L$ be a full subcomplex of
$L$ be a full subcomplex of ![]() $K$ on
$K$ on ![]() $[l]$ vertices where
$[l]$ vertices where ![]() $l \leq m$. Then
$l \leq m$. Then ![]() $L(K_1,\dots,K_l)$ is a full subcomplex of
$L(K_1,\dots,K_l)$ is a full subcomplex of ![]() $K(K_1,\dots,K_m)$.
$K(K_1,\dots,K_m)$.
Proof. This follows from Lemma 3.2.
Corollary 3.11. Let ![]() $K(K_1,\dots,K_n)$ be a substitution complex. Then each
$K(K_1,\dots,K_n)$ be a substitution complex. Then each ![]() $K_i$ is a full subcomplex on its original vertex set.
$K_i$ is a full subcomplex on its original vertex set.
Proof. As each vertex is a full subcomplex, by Lemma 3.10 ![]() $\{i\}(K_1,\dots,K_m) = K_i$ is a full subcomplex of
$\{i\}(K_1,\dots,K_m) = K_i$ is a full subcomplex of ![]() $K(K_1,\dots,K_m)$.
$K(K_1,\dots,K_m)$.
Lemma 3.12. Let ![]() $K(K_1,\dots,K_n)$ be a substitution complex. Then
$K(K_1,\dots,K_n)$ be a substitution complex. Then ![]() $K(K_1,\dots,K_n)$ contains a full subcomplex
$K(K_1,\dots,K_n)$ contains a full subcomplex ![]() $K'$, such that there is a simplicial equivalence
$K'$, such that there is a simplicial equivalence ![]() $K'=K$.
$K'=K$.
Proof. Let ![]() $v_i$ denote a vertex belonging to
$v_i$ denote a vertex belonging to ![]() $K_i$. Consider the full subcomplex on the vertex set
$K_i$. Consider the full subcomplex on the vertex set ![]() $\{v_1,\dots,v_n\} \in K(K_1,\dots,K_n)$. We will show that this is isomorphic to a copy of
$\{v_1,\dots,v_n\} \in K(K_1,\dots,K_n)$. We will show that this is isomorphic to a copy of ![]() $K$. Let
$K$. Let ![]() $\sigma = (j_1,\dots,j_k)$ be a simplex of
$\sigma = (j_1,\dots,j_k)$ be a simplex of ![]() $K$. By definition of the substitution operation,
$K$. By definition of the substitution operation, ![]() $\sigma_{j_1} \cup \dots \cup \sigma_{j_k} \in K(K_1,\dots,K_n)$ for all
$\sigma_{j_1} \cup \dots \cup \sigma_{j_k} \in K(K_1,\dots,K_n)$ for all ![]() $\sigma_{j_i} \in K_{j_i}$. Letting each
$\sigma_{j_i} \in K_{j_i}$. Letting each ![]() $\sigma_{j_i} = v_{j_i} \in K_{j_i}$, we have that
$\sigma_{j_i} = v_{j_i} \in K_{j_i}$, we have that ![]() $(v_{j_1},\dots,v_{j_k}) \in K(K_1,\dots,K_n)$. Therefore, for every simplex
$(v_{j_1},\dots,v_{j_k}) \in K(K_1,\dots,K_n)$. Therefore, for every simplex ![]() $\sigma \in K$, we have a copy
$\sigma \in K$, we have a copy ![]() $\sigma' = (v_{j_1},\dots,v_{j_k}) \in K(K_1,\dots,K_n)$, and so a copy of
$\sigma' = (v_{j_1},\dots,v_{j_k}) \in K(K_1,\dots,K_n)$, and so a copy of ![]() $K$ is contained in
$K$ is contained in ![]() $ K(K_1,\dots,K_n)$. Denote this copy
$ K(K_1,\dots,K_n)$. Denote this copy ![]() $K'$. We now show
$K'$. We now show ![]() $K'$ is a full subcomplex of
$K'$ is a full subcomplex of ![]() $K(K_1,\dots,K_n)$. Assume that
$K(K_1,\dots,K_n)$. Assume that ![]() $K'$ is not a full subcomplex, so there is a face
$K'$ is not a full subcomplex, so there is a face ![]() $\tau'$ on some subset of the vertex set
$\tau'$ on some subset of the vertex set ![]() $\{v_1,\dots,v_n\}$ that is not a face of
$\{v_1,\dots,v_n\}$ that is not a face of ![]() $K'$ but is a face of
$K'$ but is a face of ![]() $K(K_1,\dots,K_n)$. Let
$K(K_1,\dots,K_n)$. Let ![]() $\tau' = (v_{j_1},\dots,v_{j_k}) \in K(K_1,\dots,K_n)$. By definition of substitution,
$\tau' = (v_{j_1},\dots,v_{j_k}) \in K(K_1,\dots,K_n)$. By definition of substitution, ![]() $\tau = (j_1,\dots,j_k)$ is a simplex in
$\tau = (j_1,\dots,j_k)$ is a simplex in ![]() $K$. But then as there is a copy of every simplex in
$K$. But then as there is a copy of every simplex in ![]() $K$ replicated on the vertex set
$K$ replicated on the vertex set ![]() $\{v_1,\dots,v_n\}$, we have that
$\{v_1,\dots,v_n\}$, we have that ![]() $\tau'$ must be a face on the vertex set
$\tau'$ must be a face on the vertex set ![]() $\{v_1,\dots,v_n\}$, and so
$\{v_1,\dots,v_n\}$, and so ![]() $K'$ is a full subcomplex of
$K'$ is a full subcomplex of ![]() $K(K_1,\dots,K_n)$.
$K(K_1,\dots,K_n)$.
In general, the polyhedral join product does not contain a copy of the original simplex ![]() $M$ as a full subcomplex. This property is unique to the substitution complex.
$M$ as a full subcomplex. This property is unique to the substitution complex.
4. A generalised homotopy equivalence for loop spaces of certain polyhedral products
In this section, we generalise results from [Reference Theriault27]. Let ![]() $M$ be a simplicial complex on
$M$ be a simplicial complex on ![]() $[m]$, and let
$[m]$, and let ![]() $N$ be a subcomplex of
$N$ be a subcomplex of ![]() $M$. Let
$M$. Let ![]() $K$ be a simplicial complex on
$K$ be a simplicial complex on ![]() $[k]$, and let
$[k]$, and let ![]() $L$ be a subcomplex of
$L$ be a subcomplex of ![]() $K$. Consider
$K$. Consider ![]() $N$ and
$N$ and ![]() $L$ to be on the vertex sets of
$L$ to be on the vertex sets of ![]() $M$ and
$M$ and ![]() $K$, respectively. Define
$K$, respectively. Define ![]() $Q$ to be the pushout
$Q$ to be the pushout

The simplicial complex ![]() $Q$ is considered to be on the vertex set
$Q$ is considered to be on the vertex set ![]() $[m+k]$. Applying Lemma 2.7 and Lemma 2.8 gives the following result
$[m+k]$. Applying Lemma 2.7 and Lemma 2.8 gives the following result
Lemma 4.1. There exists a pushout

There are inclusion maps from ![]() $M*L$ and
$M*L$ and ![]() $N*K$ into
$N*K$ into ![]() $M*K$, and the inclusions
$M*K$, and the inclusions ![]() $M*K$ coincide on
$M*K$ coincide on ![]() $N*L$. Therefore, there is a pushout map
$N*L$. Therefore, there is a pushout map ![]() $Q \to M*K$. This induces the following pushout map on topological spaces:
$Q \to M*K$. This induces the following pushout map on topological spaces:

The maps ![]() $N * K \to M * K$ and
$N * K \to M * K$ and ![]() $M*L \to M*K$ are both the join of an inclusion and the identity, and so on the level of polyhedral products, they induce the maps
$M*L \to M*K$ are both the join of an inclusion and the identity, and so on the level of polyhedral products, they induce the maps
 \begin{equation*}{(\underline{X},\underline{A})}^{N} \times {(\underline{X},\underline{A})}^{K} \xrightarrow{g \times 1} {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*}
\begin{equation*}{(\underline{X},\underline{A})}^{N} \times {(\underline{X},\underline{A})}^{K} \xrightarrow{g \times 1} {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*}and
 \begin{equation*}{(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^L \xrightarrow{1 \times h} {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^L.\end{equation*}
\begin{equation*}{(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^L \xrightarrow{1 \times h} {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^L.\end{equation*} If all four corners of the pushout (3) are included into  ${(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K$, we obtain homotopy fibrations
${(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K$, we obtain homotopy fibrations
 \begin{equation*}F \to {(\underline{X},\underline{A})}^{Q} \xrightarrow{\Theta} {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*}
\begin{equation*}F \to {(\underline{X},\underline{A})}^{Q} \xrightarrow{\Theta} {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*} \begin{equation*}G \to {(\underline{X},\underline{A})}^{N} \times {(\underline{X},\underline{A})}^K \xrightarrow{g\times 1} {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*}
\begin{equation*}G \to {(\underline{X},\underline{A})}^{N} \times {(\underline{X},\underline{A})}^K \xrightarrow{g\times 1} {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*} \begin{equation*}H \to {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^L \xrightarrow{1 \times h} {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*}
\begin{equation*}H \to {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^L \xrightarrow{1 \times h} {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*} \begin{equation*}G \times H \to {(\underline{X},\underline{A})}^{N} \times {(\underline{X},\underline{A})}^L \xrightarrow{h \times i} {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*}
\begin{equation*}G \times H \to {(\underline{X},\underline{A})}^{N} \times {(\underline{X},\underline{A})}^L \xrightarrow{h \times i} {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*} where ![]() $F$ is the homotopy fibre of
$F$ is the homotopy fibre of ![]() $\Theta$,
$\Theta$, ![]() $G$ is the homotopy fibre of the map
$G$ is the homotopy fibre of the map ![]() $g$, and
$g$, and ![]() $H$ is the homotopy fibre of
$H$ is the homotopy fibre of ![]() $h$. As the homotopy fibres are the result of mapping each corner of the pushout into a common base, we obtain the homotopy commutative cube
$h$. As the homotopy fibres are the result of mapping each corner of the pushout into a common base, we obtain the homotopy commutative cube

in which all four sides are homotopy pullbacks. Since the bottom face is a homotopy pushout, by Lemma 2.18, the top face is a homotopy pushout.
Lemma 4.2. The maps ![]() $G \times H \to G$ and
$G \times H \to G$ and ![]() $G \times H \to H$ in (2) can be chosen to be projections, implying that there is a homotopy equivalence
$G \times H \to H$ in (2) can be chosen to be projections, implying that there is a homotopy equivalence ![]() $F \simeq G*H$.
$F \simeq G*H$.
Proof. Consider the following diagram

As the fibrations are taken over the common base  ${(\underline{X},\underline{A})}^M \times {(\underline{X},\underline{A})}^K$, the left square is the homotopy pullback appearing in the rear face of the cube. This diagram is the product of the fibration diagram for the factors on the left and the fibration diagram for the factors on the right. Observe
${(\underline{X},\underline{A})}^M \times {(\underline{X},\underline{A})}^K$, the left square is the homotopy pullback appearing in the rear face of the cube. This diagram is the product of the fibration diagram for the factors on the left and the fibration diagram for the factors on the right. Observe ![]() $* \times 1$ is the projection of the right-hand factor. Thus, the map
$* \times 1$ is the projection of the right-hand factor. Thus, the map ![]() $G \times H \to G$ is homotopic to the projection. The argument for the map
$G \times H \to G$ is homotopic to the projection. The argument for the map ![]() $G \times H \to G$ being a projection is similar. It is well known that the homotopy pushout of projections is a join, and so the homotopy pushout in the top face of the cube implies that
$G \times H \to G$ being a projection is similar. It is well known that the homotopy pushout of projections is a join, and so the homotopy pushout in the top face of the cube implies that ![]() $F \simeq G*H$.
$F \simeq G*H$.
Theorem 4.3. Let ![]() $Q$ be the pushout 2. There is a homotopy fibration
$Q$ be the pushout 2. There is a homotopy fibration
 \begin{equation*}G*H\to {(\underline{X},\underline{A})}^{Q} \to {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*}
\begin{equation*}G*H\to {(\underline{X},\underline{A})}^{Q} \to {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*} where ![]() $G$ is the homotopy fibre of
$G$ is the homotopy fibre of  ${(\underline{X},\underline{A})}^N \to {(\underline{X},\underline{A})}^{M}$ and
${(\underline{X},\underline{A})}^N \to {(\underline{X},\underline{A})}^{M}$ and ![]() $H$ is the homotopy fibre of
$H$ is the homotopy fibre of  ${(\underline{X},\underline{A})}^L \to {(\underline{X},\underline{A})}^K$. This fibration splits after looping, giving a homotopy equivalence
${(\underline{X},\underline{A})}^L \to {(\underline{X},\underline{A})}^K$. This fibration splits after looping, giving a homotopy equivalence
 \begin{equation*}\Omega{(\underline{X},\underline{A})}^{Q} \simeq \Omega{(\underline{X},\underline{A})}^{M} \times \Omega {(\underline{X},\underline{A})}^{K} \times \Omega(G*H).\end{equation*}
\begin{equation*}\Omega{(\underline{X},\underline{A})}^{Q} \simeq \Omega{(\underline{X},\underline{A})}^{M} \times \Omega {(\underline{X},\underline{A})}^{K} \times \Omega(G*H).\end{equation*}Proof. If ![]() $F$ is the homotopy fibre of the map
$F$ is the homotopy fibre of the map  $\Theta: {(\underline{X},\underline{A})}^{Q} \to {(\underline{X},\underline{A})}^M \times {(\underline{X},\underline{A})}^K$, then by Lemma 4.2,
$\Theta: {(\underline{X},\underline{A})}^{Q} \to {(\underline{X},\underline{A})}^M \times {(\underline{X},\underline{A})}^K$, then by Lemma 4.2, ![]() $F \simeq G*H$. This establishes the asserted homotopy fibration. For the splitting, consider the composite
$F \simeq G*H$. This establishes the asserted homotopy fibration. For the splitting, consider the composite  ${(\underline{X},\underline{A})}^{M} \times{(\underline{X},\underline{A})}^{L} \to {(\underline{X},\underline{A})}^{Q} \to {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^{K}$ which is
${(\underline{X},\underline{A})}^{M} \times{(\underline{X},\underline{A})}^{L} \to {(\underline{X},\underline{A})}^{Q} \to {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^{K}$ which is ![]() $1 \times h$. Restricting to
$1 \times h$. Restricting to  ${(\underline{X},\underline{A})}^{M}$ gives inclusion into the left factor. Similarly, restricting the composite
${(\underline{X},\underline{A})}^{M}$ gives inclusion into the left factor. Similarly, restricting the composite  ${(\underline{X},\underline{A})}^N \times {(\underline{X},\underline{A})}^K \to {(\underline{X},\underline{A})}^{Q} \to {(\underline{X},\underline{A})}^M \times {(\underline{X},\underline{A})}^K$ to
${(\underline{X},\underline{A})}^N \times {(\underline{X},\underline{A})}^K \to {(\underline{X},\underline{A})}^{Q} \to {(\underline{X},\underline{A})}^M \times {(\underline{X},\underline{A})}^K$ to  ${(\underline{X},\underline{A})}^K$ gives inclusion into the right factor. Taking the wedge sum of these therefore gives the composite
${(\underline{X},\underline{A})}^K$ gives inclusion into the right factor. Taking the wedge sum of these therefore gives the composite
 \begin{equation*}{(\underline{X},\underline{A})}^{M} \vee {(\underline{X},\underline{A})}^K \to {(\underline{X},\underline{A})}^{Q} \to {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*}
\begin{equation*}{(\underline{X},\underline{A})}^{M} \vee {(\underline{X},\underline{A})}^K \to {(\underline{X},\underline{A})}^{Q} \to {(\underline{X},\underline{A})}^{M} \times {(\underline{X},\underline{A})}^K\end{equation*} which is the inclusion of the wedge into the product. The inclusion of the wedge into the product has a right homotopy inverse after looping, so the map  $\Omega{(\underline{X},\underline{A})}^{Q} \to \Omega{(\underline{X},\underline{A})}^{M} \times \Omega{(\underline{X},\underline{A})}^K$ has a right homotopy inverse, implying that the fibration splits after looping.
$\Omega{(\underline{X},\underline{A})}^{Q} \to \Omega{(\underline{X},\underline{A})}^{M} \times \Omega{(\underline{X},\underline{A})}^K$ has a right homotopy inverse, implying that the fibration splits after looping.
5. Loop spaces of polyhedral products associated with polyhedral join products
In this section, we apply Theorem 4.3 to the polyhedral join product. By Corollary 3.6, there exists a pushout

This is a special case of the pushout in 2, where  $N = {(\underline{K},\underline{L})}^{*\mathrm{lk}_M(m)}$,
$N = {(\underline{K},\underline{L})}^{*\mathrm{lk}_M(m)}$, ![]() $L = L_m$,
$L = L_m$,  $M = {(\underline{K},\underline{L})}^{*M \setminus m}$ and
$M = {(\underline{K},\underline{L})}^{*M \setminus m}$ and ![]() $K = K_m$. Applying Theorem 4.3, we obtain a homotopy equivalence
$K = K_m$. Applying Theorem 4.3, we obtain a homotopy equivalence
 \begin{equation*}\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \simeq \Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus m}} \times \Omega {(\underline{X},\underline{A})}^{K_m} \times \Omega(G_m*H_m),\end{equation*}
\begin{equation*}\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \simeq \Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus m}} \times \Omega {(\underline{X},\underline{A})}^{K_m} \times \Omega(G_m*H_m),\end{equation*} where ![]() $G_m$ is the homotopy fibre of the map
$G_m$ is the homotopy fibre of the map  ${(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*\mathrm{lk}_M(m)}} \to {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus m}}$ and
${(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*\mathrm{lk}_M(m)}} \to {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus m}}$ and ![]() $H_m$ is the homotopy fibre of the map
$H_m$ is the homotopy fibre of the map  ${(\underline{X},\underline{A})}^{L_m} \to {(\underline{X},\underline{A})}^{K_m}$. By iterating this homotopy equivalence with respect to the vertices of
${(\underline{X},\underline{A})}^{L_m} \to {(\underline{X},\underline{A})}^{K_m}$. By iterating this homotopy equivalence with respect to the vertices of ![]() $M$, we prove Theorem 1.1.
$M$, we prove Theorem 1.1.
Proof of Theorem 1.1
By Theorem 4.3, there is a homotopy equivalence
 \begin{equation*}\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \simeq \Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus m}} \times \Omega {(\underline{X},\underline{A})}^{K_m} \times \Omega(G_m*H_m).\end{equation*}
\begin{equation*}\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \simeq \Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus m}} \times \Omega {(\underline{X},\underline{A})}^{K_m} \times \Omega(G_m*H_m).\end{equation*} Now consider  ${(\underline{K},\underline{L})}^{*M \setminus m}$. If
${(\underline{K},\underline{L})}^{*M \setminus m}$. If ![]() $M \setminus m$ is a simplex, then by Example 3.1,
$M \setminus m$ is a simplex, then by Example 3.1,  ${(\underline{K},\underline{L})}^{*M \setminus m} = K_1*\dots*K_{m-1}$, and so
${(\underline{K},\underline{L})}^{*M \setminus m} = K_1*\dots*K_{m-1}$, and so  ${(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus m}} \simeq {(\underline{X},\underline{A})}^{K_1} \times \dots \times {(\underline{X},\underline{A})}^{K_{m-1}}$, and the result follows. If not, the simplicial complex
${(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus m}} \simeq {(\underline{X},\underline{A})}^{K_1} \times \dots \times {(\underline{X},\underline{A})}^{K_{m-1}}$, and the result follows. If not, the simplicial complex  ${(\underline{K},\underline{L})}^{*M \setminus m}$ is a polyhedral join product, and therefore can be constructed as in 2, with
${(\underline{K},\underline{L})}^{*M \setminus m}$ is a polyhedral join product, and therefore can be constructed as in 2, with  $N = {(\underline{K},\underline{L})}^{*\mathrm{lk}_{M\setminus m}(m-1)}$,
$N = {(\underline{K},\underline{L})}^{*\mathrm{lk}_{M\setminus m}(m-1)}$, ![]() $L = L_{m-1}$,
$L = L_{m-1}$,  $M = {(\underline{K},\underline{L})}^{* M \setminus \{m,m-1\}}$ and
$M = {(\underline{K},\underline{L})}^{* M \setminus \{m,m-1\}}$ and ![]() $K = K_{m-1}$. We can apply Theorem 4.3 to
$K = K_{m-1}$. We can apply Theorem 4.3 to  ${(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus m}}$ to obtain a homotopy equivalence
${(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus m}}$ to obtain a homotopy equivalence
 \begin{equation*}\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus m}} \simeq \Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus \{m,m-1\}}} \times \Omega {(\underline{X},\underline{A})}^{K_{m-1}} \times \Omega(G_{m-1}*H_{m-1}).\end{equation*}
\begin{equation*}\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus m}} \simeq \Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus \{m,m-1\}}} \times \Omega {(\underline{X},\underline{A})}^{K_{m-1}} \times \Omega(G_{m-1}*H_{m-1}).\end{equation*}Substituting this into our previous expression gives a homotopy equivalence
 \begin{equation*}\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \simeq \Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus \{m,m-1\}}} \times \prod_{i=m-1}^m \Omega {(\underline{X},\underline{A})}^{K_{i}} \times \prod_{j=m+1}^m \Omega(G_{j}*H_{j}).\end{equation*}
\begin{equation*}\Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \simeq \Omega {(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus \{m,m-1\}}} \times \prod_{i=m-1}^m \Omega {(\underline{X},\underline{A})}^{K_{i}} \times \prod_{j=m+1}^m \Omega(G_{j}*H_{j}).\end{equation*} We continue this process on  ${(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus \{m,m-1\}}}$ until we reach the vertex
${(\underline{X},\underline{A})}^{{(\underline{K},\underline{L})}^{*M \setminus \{m,m-1\}}}$ until we reach the vertex ![]() $k$ such that
$k$ such that ![]() $M \setminus \{m,\dots,k\}$ is a simplex.
$M \setminus \{m,\dots,k\}$ is a simplex.
6. Simplicial operations preserving the property of being in  ${\mathcal{P}}$
${\mathcal{P}}$
Recall that ![]() ${\mathcal{P}}$ is the full subcategory of topological spaces that are homotopy equivalent to a product of spheres and loops on spheres. Restricting to the case where
${\mathcal{P}}$ is the full subcategory of topological spaces that are homotopy equivalent to a product of spheres and loops on spheres. Restricting to the case where ![]() ${(\underline{X},\underline{A})} = {(\underline{CA},\underline{A})}$, let
${(\underline{X},\underline{A})} = {(\underline{CA},\underline{A})}$, let ![]() $M$ be a simplicial complex such that
$M$ be a simplicial complex such that  $\Omega {(\underline{CA},\underline{A})}^M \in {\mathcal{P}}$. The polyhedral join product
$\Omega {(\underline{CA},\underline{A})}^M \in {\mathcal{P}}$. The polyhedral join product  ${(\underline{K},\underline{L})}^{*M}$ can be considered as an operation on simplicial complexes, and as such, it is natural to ask when such an operation preserves the property of having a loop space on an associated polyhedral product in
${(\underline{K},\underline{L})}^{*M}$ can be considered as an operation on simplicial complexes, and as such, it is natural to ask when such an operation preserves the property of having a loop space on an associated polyhedral product in ![]() ${\mathcal{P}}$. In this section, we give some general conditions that ensure
${\mathcal{P}}$. In this section, we give some general conditions that ensure  $\Omega{(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$. We then determine that for the substitution complex and the composition complex, we can guarantee some of these conditions will always be met.
$\Omega{(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$. We then determine that for the substitution complex and the composition complex, we can guarantee some of these conditions will always be met.
Theorem 6.1. Let ![]() $M$ be a simplicial complex on the vertex set
$M$ be a simplicial complex on the vertex set ![]() $[m]$, let
$[m]$, let ![]() $K_i$ be a simplicial complex on the vertex set
$K_i$ be a simplicial complex on the vertex set ![]() $[k_i]$, and let
$[k_i]$, and let ![]() $L_i \subseteq K_i$ be a subcomplex of
$L_i \subseteq K_i$ be a subcomplex of ![]() $K_i$ for all
$K_i$ for all ![]() $i \in [m]$. Let
$i \in [m]$. Let ![]() ${(\underline{CA},\underline{A})}$ be a sequence of pairs
${(\underline{CA},\underline{A})}$ be a sequence of pairs ![]() $(CA_j,A_j)$ where
$(CA_j,A_j)$ where ![]() $j \in [m -1 + k_i]$. Suppose
$j \in [m -1 + k_i]$. Suppose ![]() $\Sigma A_j \in {\mathcal{W}}$ for all
$\Sigma A_j \in {\mathcal{W}}$ for all ![]() $j \in [m -1 + k_i]$. Suppose
$j \in [m -1 + k_i]$. Suppose  $\Omega {(\underline{CA},\underline{A})}^M \in {\mathcal{P}}$, and let
$\Omega {(\underline{CA},\underline{A})}^M \in {\mathcal{P}}$, and let ![]() $Q$ be the simplicial complex defined by the following pushout
$Q$ be the simplicial complex defined by the following pushout

Let ![]() $H_i$ be the homotopy fibre of the map
$H_i$ be the homotopy fibre of the map  ${(\underline{CA},\underline{A})}^{L_i} \to {(\underline{CA},\underline{A})}^{K_i}$ where
${(\underline{CA},\underline{A})}^{L_i} \to {(\underline{CA},\underline{A})}^{K_i}$ where ![]() $L_i$ is considered on the vertex set
$L_i$ is considered on the vertex set ![]() $K_i$, and let
$K_i$, and let ![]() $G_i$ be the homotopy fibre of the map
$G_i$ be the homotopy fibre of the map  ${(\underline{CA},\underline{A})}^{L_i} \to {(\underline{CA},\underline{A})}^{K_i}$. If
${(\underline{CA},\underline{A})}^{L_i} \to {(\underline{CA},\underline{A})}^{K_i}$. If  $\Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{P}}$ and
$\Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{P}}$ and ![]() $\Sigma H_i \in {\mathcal{W}}$ then
$\Sigma H_i \in {\mathcal{W}}$ then  $\Omega {(\underline{CA},\underline{A})}^{Q} \in {\mathcal{P}}$.
$\Omega {(\underline{CA},\underline{A})}^{Q} \in {\mathcal{P}}$.
Proof. Applying Lemma 2.13 to  ${(\underline{CA},\underline{A})}^M$ gives
${(\underline{CA},\underline{A})}^M$ gives  $\Omega {(\underline{CA},\underline{A})}^{M} \simeq \Omega {(\underline{CA},\underline{A})}^{M \setminus i} \times \Omega (\Sigma G_i \wedge A_i)$. As
$\Omega {(\underline{CA},\underline{A})}^{M} \simeq \Omega {(\underline{CA},\underline{A})}^{M \setminus i} \times \Omega (\Sigma G_i \wedge A_i)$. As  $\Omega {(\underline{CA},\underline{A})}^M \in {\mathcal{P}}$, and both
$\Omega {(\underline{CA},\underline{A})}^M \in {\mathcal{P}}$, and both  $\Omega {(\underline{CA},\underline{A})}^{M\setminus i}$ and
$\Omega {(\underline{CA},\underline{A})}^{M\setminus i}$ and ![]() $\Omega (\Sigma G_i \wedge A_i)$ retract off
$\Omega (\Sigma G_i \wedge A_i)$ retract off  $\Omega {(\underline{CA},\underline{A})}^M$ by Lemma 2.5 both
$\Omega {(\underline{CA},\underline{A})}^M$ by Lemma 2.5 both  $\Omega {(\underline{CA},\underline{A})}^{M\setminus i}$ and
$\Omega {(\underline{CA},\underline{A})}^{M\setminus i}$ and ![]() $\Omega (\Sigma G_i \wedge A_i)$ are in
$\Omega (\Sigma G_i \wedge A_i)$ are in ![]() ${\mathcal{P}}$. By Lemma 2.6,
${\mathcal{P}}$. By Lemma 2.6, ![]() $\Sigma (G_i \wedge A_i) \in {\mathcal{W}}$. Now consider
$\Sigma (G_i \wedge A_i) \in {\mathcal{W}}$. Now consider  ${(\underline{CA},\underline{A})}^{Q}$. Applying Theorem 4.3 gives
${(\underline{CA},\underline{A})}^{Q}$. Applying Theorem 4.3 gives
 \begin{equation*}\Omega {(\underline{CA},\underline{A})}^{Q} \simeq \Omega {(\underline{CA},\underline{A})}^{M \setminus i} \times \Omega{(\underline{CA},\underline{A})}^{K_i} \times \Omega(\Sigma G_i \wedge H_i).\end{equation*}
\begin{equation*}\Omega {(\underline{CA},\underline{A})}^{Q} \simeq \Omega {(\underline{CA},\underline{A})}^{M \setminus i} \times \Omega{(\underline{CA},\underline{A})}^{K_i} \times \Omega(\Sigma G_i \wedge H_i).\end{equation*} As ![]() $\Sigma H_i \in {\mathcal{W}}$, and
$\Sigma H_i \in {\mathcal{W}}$, and ![]() $\Sigma H_i$ is at least as connected as
$\Sigma H_i$ is at least as connected as ![]() $\Sigma A_i$ by Lemma 2.17,
$\Sigma A_i$ by Lemma 2.17, ![]() $\Sigma G_i \wedge H_i \in {\mathcal{W}}$. Therefore,
$\Sigma G_i \wedge H_i \in {\mathcal{W}}$. Therefore, ![]() $\Omega\Sigma (G_i \wedge H_i) \in {\mathcal{P}}$ by Lemma 2.2. Hence, each element on the right-hand side of the homotopy equivalence is in
$\Omega\Sigma (G_i \wedge H_i) \in {\mathcal{P}}$ by Lemma 2.2. Hence, each element on the right-hand side of the homotopy equivalence is in ![]() ${\mathcal{P}}$, and therefore
${\mathcal{P}}$, and therefore  $\Omega {(\underline{CA},\underline{A})}^{Q} \in {\mathcal{P}}$.
$\Omega {(\underline{CA},\underline{A})}^{Q} \in {\mathcal{P}}$.
Recall that by Lemma 3.9, the polyhedral join product can be constructed sequentially via an iterated pushout construction. More specifically, there is a sequence of simplicial complexes
 \begin{equation*}M \subset M(1) \subset M(2) \subset \dots \subset M(m) = {(\underline{K},\underline{L})}^{*M}\end{equation*}
\begin{equation*}M \subset M(1) \subset M(2) \subset \dots \subset M(m) = {(\underline{K},\underline{L})}^{*M}\end{equation*} where at each point, ![]() $M(i+1)$ is obtained from
$M(i+1)$ is obtained from ![]() $M(i)$ via the pushout
$M(i)$ via the pushout

This, combined with Theorem 6.1, allows us to prove Theorem 1.2.
Proof of Theorem 1.2
We proceed by induction on ![]() $M(i)$. The base case is
$M(i)$. The base case is ![]() $M(1)$. The simplicial complex
$M(1)$. The simplicial complex ![]() $M(1)$ is defined as the pushout
$M(1)$ is defined as the pushout

By assumption  $\Omega {(\underline{CA},\underline{A})}^{K_1} \in {\mathcal{P}}$, and
$\Omega {(\underline{CA},\underline{A})}^{K_1} \in {\mathcal{P}}$, and ![]() $\Sigma H_1 \in {\mathcal{W}}$ and so by Theorem 6.1, we obtain
$\Sigma H_1 \in {\mathcal{W}}$ and so by Theorem 6.1, we obtain  $\Omega {(\underline{CA},\underline{A})}^{M(1)} \in {\mathcal{P}}$. Now suppose that for all
$\Omega {(\underline{CA},\underline{A})}^{M(1)} \in {\mathcal{P}}$. Now suppose that for all ![]() $j \lt i$,
$j \lt i$,  $\Omega {(\underline{CA},\underline{A})}^{M(i)} \in {\mathcal{P}}$. Consider
$\Omega {(\underline{CA},\underline{A})}^{M(i)} \in {\mathcal{P}}$. Consider ![]() $M(i)$. This simplicial complex is defined by the pushout
$M(i)$. This simplicial complex is defined by the pushout

By induction,  $\Omega {(\underline{CA},\underline{A})}^{M(i-1)} \in {\mathcal{P}}$, and by assumption,
$\Omega {(\underline{CA},\underline{A})}^{M(i-1)} \in {\mathcal{P}}$, and by assumption,  $\Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{P}}$ and
$\Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{P}}$ and ![]() $\Sigma H_i \in {\mathcal{W}}$. Therefore, we can apply Theorem 6.1, with
$\Sigma H_i \in {\mathcal{W}}$. Therefore, we can apply Theorem 6.1, with ![]() $M = M(i-1)$ to obtain
$M = M(i-1)$ to obtain  $\Omega {(\underline{CA},\underline{A})}^{M(i)} \in {\mathcal{P}}$. Therefore,
$\Omega {(\underline{CA},\underline{A})}^{M(i)} \in {\mathcal{P}}$. Therefore,  $\Omega {(\underline{CA},\underline{A})}^{M(i)} \in {\mathcal{P}}$ for all
$\Omega {(\underline{CA},\underline{A})}^{M(i)} \in {\mathcal{P}}$ for all ![]() $i \in [m]$ by induction. When
$i \in [m]$ by induction. When ![]() $i=m$ by definition
$i=m$ by definition  $M(m) = {(\underline{K},\underline{L})}^{*M}$, and so the result holds.
$M(m) = {(\underline{K},\underline{L})}^{*M}$, and so the result holds.
Theorem 1.2 tells us that given ![]() $M$ such that
$M$ such that  $\Omega {(\underline{CA},\underline{A})}^{M} \in {\mathcal{P}}$, we can construct a new simplicial complex
$\Omega {(\underline{CA},\underline{A})}^{M} \in {\mathcal{P}}$, we can construct a new simplicial complex  ${(\underline{K},\underline{L})}^{*M}$ such that
${(\underline{K},\underline{L})}^{*M}$ such that  $\Omega {(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$, subject to conditions on
$\Omega {(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$, subject to conditions on ![]() $K_i$ and the homotopy fibre
$K_i$ and the homotopy fibre ![]() $H_i$. Guaranteeing
$H_i$. Guaranteeing ![]() $\Sigma H_i \in W$ is not so simple. We can give conditions on the map
$\Sigma H_i \in W$ is not so simple. We can give conditions on the map  ${(\underline{CA},\underline{A})}^{L_i} \to {(\underline{CA},\underline{A})}^{K_i}$ to ensure
${(\underline{CA},\underline{A})}^{L_i} \to {(\underline{CA},\underline{A})}^{K_i}$ to ensure ![]() $\Sigma H_i \in {\mathcal{W}}$.
$\Sigma H_i \in {\mathcal{W}}$.
Lemma 6.2. Let ![]() $M$ be a simplicial complex on
$M$ be a simplicial complex on ![]() $[m]$ vertices. Let
$[m]$ vertices. Let  ${(\underline{K},\underline{L})}^{*M}$ be a polyhedral join product and let
${(\underline{K},\underline{L})}^{*M}$ be a polyhedral join product and let ![]() $K_i$ be a simplicial complex on the vertex set
$K_i$ be a simplicial complex on the vertex set ![]() $[k_i]$ for
$[k_i]$ for ![]() $i \in [m]$. Let
$i \in [m]$. Let ![]() ${(\underline{CA},\underline{A})}$ be a sequence of pairs
${(\underline{CA},\underline{A})}$ be a sequence of pairs ![]() $(CA_j,A_j)$ where
$(CA_j,A_j)$ where ![]() $1 \leq j \leq k_1 + \dots + k_m$. Suppose the pairs
$1 \leq j \leq k_1 + \dots + k_m$. Suppose the pairs ![]() ${(\underline{K},\underline{L})}$ are such that the map
${(\underline{K},\underline{L})}$ are such that the map  ${(\underline{CA},\underline{A})}^{L_i} \to {(\underline{CA},\underline{A})}^{K_i}$ is null homotopic. If
${(\underline{CA},\underline{A})}^{L_i} \to {(\underline{CA},\underline{A})}^{K_i}$ is null homotopic. If  $\Sigma {(\underline{CA},\underline{A})}^{L_i} \in {\mathcal{W}}$ and
$\Sigma {(\underline{CA},\underline{A})}^{L_i} \in {\mathcal{W}}$ and  $\Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{P}}$ for all
$\Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{P}}$ for all ![]() $i$, then
$i$, then  $\Omega {(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$.
$\Omega {(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$.
Proof. As the map  ${(\underline{CA},\underline{A})}^{L_i} \to {(\underline{CA},\underline{A})}^{K_i}$ is null homotopic, its homotopy fibre, denoted
${(\underline{CA},\underline{A})}^{L_i} \to {(\underline{CA},\underline{A})}^{K_i}$ is null homotopic, its homotopy fibre, denoted ![]() $H_i$, will be homotopy equivalent to
$H_i$, will be homotopy equivalent to  ${(\underline{CA},\underline{A})}^{L_i} \times \Omega {(\underline{CA},\underline{A})}^{K_i}$. Therefore,
${(\underline{CA},\underline{A})}^{L_i} \times \Omega {(\underline{CA},\underline{A})}^{K_i}$. Therefore,
 \begin{equation*}\Sigma H_i \simeq \Sigma {(\underline{CA},\underline{A})}^{L_i} \vee \Sigma \Omega {(\underline{CA},\underline{A})}^{K_i} \vee \Sigma ({(\underline{CA},\underline{A})}^{L_i} \wedge \Omega {(\underline{CA},\underline{A})}^{K_i}).\end{equation*}
\begin{equation*}\Sigma H_i \simeq \Sigma {(\underline{CA},\underline{A})}^{L_i} \vee \Sigma \Omega {(\underline{CA},\underline{A})}^{K_i} \vee \Sigma ({(\underline{CA},\underline{A})}^{L_i} \wedge \Omega {(\underline{CA},\underline{A})}^{K_i}).\end{equation*} As  $\Sigma {(\underline{CA},\underline{A})}^{L_i} \in {\mathcal{W}}$ by assumption, and
$\Sigma {(\underline{CA},\underline{A})}^{L_i} \in {\mathcal{W}}$ by assumption, and  $\Sigma \Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{W}}$ by Lemma 2.12, all elements on the right-hand side are in
$\Sigma \Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{W}}$ by Lemma 2.12, all elements on the right-hand side are in ![]() ${\mathcal{W}}$. Therefore, we have
${\mathcal{W}}$. Therefore, we have ![]() $\Sigma H_i \in {\mathcal{W}}$. By Theorem 1.2, then
$\Sigma H_i \in {\mathcal{W}}$. By Theorem 1.2, then  $\Omega {(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$.
$\Omega {(\underline{CA},\underline{A})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$.
The conditions laid out in Lemma 6.2 are generally easy to fulfil. For example, the pairs  $(\Delta^{n_i-1}_k,\Delta^{n_i-1}_{k-1})$ satisfy such a condition, as
$(\Delta^{n_i-1}_k,\Delta^{n_i-1}_{k-1})$ satisfy such a condition, as  ${(\underline{CA},\underline{A})}^{\Delta^{n-1}_k} \in {\mathcal{W}}$ for
${(\underline{CA},\underline{A})}^{\Delta^{n-1}_k} \in {\mathcal{W}}$ for ![]() $0 \leq k \leq n-1$ ([Reference Iriye and Kishimoto17, Theorem 1.7]), and the map
$0 \leq k \leq n-1$ ([Reference Iriye and Kishimoto17, Theorem 1.7]), and the map  ${(\underline{CA},\underline{A})}^{\Delta^{n-1}_k} \to {(\underline{CA},\underline{A})}^{\Delta^{n-1}_{k+1}}$ is null homotopic ([Reference Porter22, Lemma 8]). Recall that by [Reference Bahri, Bendersky, Cohen and Gitler6, Theorem 2.21] there is a homotopy equivalence
${(\underline{CA},\underline{A})}^{\Delta^{n-1}_k} \to {(\underline{CA},\underline{A})}^{\Delta^{n-1}_{k+1}}$ is null homotopic ([Reference Porter22, Lemma 8]). Recall that by [Reference Bahri, Bendersky, Cohen and Gitler6, Theorem 2.21] there is a homotopy equivalence
 \begin{equation*}\Sigma{(\underline{CA},\underline{A})}^K \simeq \Sigma \big(\bigvee_{I \notin K} |K_I|*\widehat{A}^I \big).\end{equation*}
\begin{equation*}\Sigma{(\underline{CA},\underline{A})}^K \simeq \Sigma \big(\bigvee_{I \notin K} |K_I|*\widehat{A}^I \big).\end{equation*} Therefore, if for all ![]() $I \notin K$,
$I \notin K$, ![]() $|K_I| \in {\mathcal{W}}$ and
$|K_I| \in {\mathcal{W}}$ and ![]() $\Sigma A_i \in {\mathcal{W}}$ for all
$\Sigma A_i \in {\mathcal{W}}$ for all ![]() $i \in [m]$, then
$i \in [m]$, then  $\Sigma{(\underline{CA},\underline{A})}^K \in {\mathcal{W}}$.
$\Sigma{(\underline{CA},\underline{A})}^K \in {\mathcal{W}}$.
More generally, we can show that the substitution complex satisfies this condition. We first require the following proposition.
Proposition 6.3. ([Reference Grbić and Theriault16, Corollary 3.5])
Let ![]() $K$ be a simplicial complex on the vertex set
$K$ be a simplicial complex on the vertex set ![]() $[m]$, and assume
$[m]$, and assume ![]() $K$ has no ghost vertices. Then the inclusion
$K$ has no ghost vertices. Then the inclusion  $\prod^m_{i=1} A_i \to {(\underline{CA},\underline{A})}^K$ is null homotopic, and the homotopy fibre of this map is
$\prod^m_{i=1} A_i \to {(\underline{CA},\underline{A})}^K$ is null homotopic, and the homotopy fibre of this map is  $\big(\prod^m_{i=1} A_i \big)\times \Omega {(\underline{CA},\underline{A})}^{K}$.
$\big(\prod^m_{i=1} A_i \big)\times \Omega {(\underline{CA},\underline{A})}^{K}$.
Lemma 6.4. Let the sequence of pairs ![]() ${(\underline{CA},\underline{A})}$ be as in Theorem 1.2. Let
${(\underline{CA},\underline{A})}$ be as in Theorem 1.2. Let ![]() $K(K_1,\dots,K_m)$ be a substitution complex. If
$K(K_1,\dots,K_m)$ be a substitution complex. If  $\Omega {(\underline{CA},\underline{A})}^K \in \mathcal{P}$ and for all
$\Omega {(\underline{CA},\underline{A})}^K \in \mathcal{P}$ and for all ![]() $i \in [m]$ we have
$i \in [m]$ we have  $\Omega {(\underline{CA},\underline{A})}^{K_i}\in {\mathcal{P}}$, then
$\Omega {(\underline{CA},\underline{A})}^{K_i}\in {\mathcal{P}}$, then  $\Omega {(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \in{\mathcal{P}}$.
$\Omega {(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \in{\mathcal{P}}$.
Proof. Recall that the substitution complex is a special case of the polyhedral join product on the simplicial pairs ![]() $(K_i, \emptyset)$. Therefore,
$(K_i, \emptyset)$. Therefore, ![]() $H_i$ is the homotopy fibre of the map
$H_i$ is the homotopy fibre of the map  $\prod_{j \in K_i} A_j \to {(\underline{CA},\underline{A})}^{K_i}$. By Lemma 6.3, this map is null homotopic. As by assumption,
$\prod_{j \in K_i} A_j \to {(\underline{CA},\underline{A})}^{K_i}$. By Lemma 6.3, this map is null homotopic. As by assumption, ![]() $\Sigma A_j \in {\mathcal{W}}$ for all
$\Sigma A_j \in {\mathcal{W}}$ for all ![]() $j$, the conditions of Lemma 6.2 are satisfied, and
$j$, the conditions of Lemma 6.2 are satisfied, and  $\Omega {(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \in {\mathcal{P}}$.
$\Omega {(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \in {\mathcal{P}}$.
Lemma 6.5. Let the sequence of pairs ![]() ${(\underline{CA},\underline{A})}$ be as in Theorem 1.2. Let
${(\underline{CA},\underline{A})}$ be as in Theorem 1.2. Let ![]() $K \langle K_1 ,\dots, K_m \rangle$ be a composition complex. If
$K \langle K_1 ,\dots, K_m \rangle$ be a composition complex. If  $\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$ and for all
$\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$ and for all ![]() $i \in [m]$ we have
$i \in [m]$ we have  $\Sigma {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{W}}$, then
$\Sigma {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{W}}$, then  $\Omega {(\underline{CA},\underline{A})}^{K\langle K_1,\dots,K_m\rangle} \in {\mathcal{P}}$.
$\Omega {(\underline{CA},\underline{A})}^{K\langle K_1,\dots,K_m\rangle} \in {\mathcal{P}}$.
Proof. Recall that the composition complex is a special case of the polyhedral join product on the simplicial pairs ![]() $(\Delta^{[k_i-1]}, K_i)$. Therefore,
$(\Delta^{[k_i-1]}, K_i)$. Therefore, ![]() $H_i$ is the homotopy fibre of the map
$H_i$ is the homotopy fibre of the map  ${(\underline{CA},\underline{A})}^{K_i} \to \prod_{j \in K_i} CA_j$. As
${(\underline{CA},\underline{A})}^{K_i} \to \prod_{j \in K_i} CA_j$. As  $\prod_{j \in K_i} CA_j$ is contractible, this map is null homotopic, so
$\prod_{j \in K_i} CA_j$ is contractible, this map is null homotopic, so  $H_i \simeq {(\underline{CA},\underline{A})}^{K_i}$. By assumption
$H_i \simeq {(\underline{CA},\underline{A})}^{K_i}$. By assumption  $\Sigma {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{W}}$, and so by Lemma 6.2,
$\Sigma {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{W}}$, and so by Lemma 6.2,  $\Omega {(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \in {\mathcal{P}}$.
$\Omega {(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \in {\mathcal{P}}$.
There are other pairs of simplicial complexes ![]() ${(\underline{K},\underline{L})}$ for which we can determine if
${(\underline{K},\underline{L})}$ for which we can determine if ![]() $\Sigma H_i \in {\mathcal{W}}$.
$\Sigma H_i \in {\mathcal{W}}$.
Proposition 6.6. Suppose ![]() ${(\underline{K},\underline{L})}$ are pairs such that for each
${(\underline{K},\underline{L})}$ are pairs such that for each ![]() $i \in [m]$, the simplicial complex
$i \in [m]$, the simplicial complex ![]() $L_i$ is a full subcomplex of
$L_i$ is a full subcomplex of ![]() $K_i$. Let
$K_i$. Let ![]() ${(\underline{C\Omega X},\underline{\Omega X})}$ be a sequence of pairs where
${(\underline{C\Omega X},\underline{\Omega X})}$ be a sequence of pairs where ![]() $\Omega X_i \in {\mathcal{P}}$ for all
$\Omega X_i \in {\mathcal{P}}$ for all ![]() $i \in [m]$. Suppose
$i \in [m]$. Suppose  $\Omega {(\underline{C\Omega X},\underline{\Omega X})}^{M} \in {\mathcal{P}}$, and suppose
$\Omega {(\underline{C\Omega X},\underline{\Omega X})}^{M} \in {\mathcal{P}}$, and suppose  ${(\underline{C\Omega X},\underline{\Omega X})}^{K_i} \in {\mathcal{P}}$ for all
${(\underline{C\Omega X},\underline{\Omega X})}^{K_i} \in {\mathcal{P}}$ for all ![]() $i \in [m]$. Then
$i \in [m]$. Then  $\Omega {(\underline{C\Omega X},\underline{\Omega X})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$.
$\Omega {(\underline{C\Omega X},\underline{\Omega X})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$.
Proof. To apply Theorem 1.2 we need to show ![]() $\Sigma H_i$, the homotopy fibre of the map
$\Sigma H_i$, the homotopy fibre of the map  ${(\underline{C\Omega X},\underline{\Omega X})}^{L_i} \to {(\underline{C\Omega X},\underline{\Omega X})}^{K_i}$ is an element of
${(\underline{C\Omega X},\underline{\Omega X})}^{L_i} \to {(\underline{C\Omega X},\underline{\Omega X})}^{K_i}$ is an element of ![]() ${\mathcal{W}}$. First consider
${\mathcal{W}}$. First consider  $\Omega {(\underline{X},\underline{\ast})}^M$. By [Reference Theriault25, Corollory 3.14, Lemma 3.16] there is a homotopy fibration
$\Omega {(\underline{X},\underline{\ast})}^M$. By [Reference Theriault25, Corollory 3.14, Lemma 3.16] there is a homotopy fibration
 \begin{equation*}{(\underline{C\Omega X},\underline{\Omega X})}^M \to {(\underline{X},\underline{\ast})}^M \to \prod_{i=1}^m X_i\end{equation*}
\begin{equation*}{(\underline{C\Omega X},\underline{\Omega X})}^M \to {(\underline{X},\underline{\ast})}^M \to \prod_{i=1}^m X_i\end{equation*}that splits after looping
 \begin{equation*}\Omega {(\underline{X},\underline{\ast})}^M \simeq \prod_{i=1}^m \Omega X_i \times \Omega {(\underline{C\Omega X},\underline{\Omega X})}^M.\end{equation*}
\begin{equation*}\Omega {(\underline{X},\underline{\ast})}^M \simeq \prod_{i=1}^m \Omega X_i \times \Omega {(\underline{C\Omega X},\underline{\Omega X})}^M.\end{equation*} As every element on the right-hand side of this homotopy equivalence is in ![]() ${\mathcal{P}}$, we obtain
${\mathcal{P}}$, we obtain  $\Omega {(\underline{X},\underline{\ast})}^M \in {\mathcal{P}}$. Via an identical argument,
$\Omega {(\underline{X},\underline{\ast})}^M \in {\mathcal{P}}$. Via an identical argument,  $\Omega {(\underline{X},\underline{\ast})}^{K_i} \in {\mathcal{P}}$ for all
$\Omega {(\underline{X},\underline{\ast})}^{K_i} \in {\mathcal{P}}$ for all ![]() $i \in [m]$. Let
$i \in [m]$. Let ![]() $F_i$ denote the homotopy fibre of
$F_i$ denote the homotopy fibre of  ${(\underline{X},\underline{\ast})}^{L_i} \to {(\underline{X},\underline{\ast})}^{K_i}$. As
${(\underline{X},\underline{\ast})}^{L_i} \to {(\underline{X},\underline{\ast})}^{K_i}$. As ![]() $L_i$ is a full subcomplex of
$L_i$ is a full subcomplex of ![]() $K_i$, by Lemma 2.10 this map has a left homotopy inverse, and so the connecting map
$K_i$, by Lemma 2.10 this map has a left homotopy inverse, and so the connecting map  $\delta: \Omega {(\underline{X},\underline{\ast})}^{K_i} \to F_i$ has a right homotopy inverse. We therefore have a homotopy equivalence
$\delta: \Omega {(\underline{X},\underline{\ast})}^{K_i} \to F_i$ has a right homotopy inverse. We therefore have a homotopy equivalence  $\Omega {(\underline{X},\underline{\ast})}^{K_i} \simeq \Omega {(\underline{X},\underline{\ast})}^{L_i} \times F_i$. If
$\Omega {(\underline{X},\underline{\ast})}^{K_i} \simeq \Omega {(\underline{X},\underline{\ast})}^{L_i} \times F_i$. If  $\Omega {(\underline{X},\underline{\ast})}^{K_i} \in {\mathcal{P}}$, by Lemma 2.5
$\Omega {(\underline{X},\underline{\ast})}^{K_i} \in {\mathcal{P}}$, by Lemma 2.5 ![]() $F_i$ is also in
$F_i$ is also in ![]() ${\mathcal{P}}$. By Lemma 2.3,
${\mathcal{P}}$. By Lemma 2.3, ![]() $\Sigma F_i$ must therefore be in
$\Sigma F_i$ must therefore be in ![]() ${\mathcal{W}}$. Now we can determine the homotopy type of
${\mathcal{W}}$. Now we can determine the homotopy type of ![]() $\Sigma H_i$. Consider the following homotopy fibration diagram
$\Sigma H_i$. Consider the following homotopy fibration diagram

where the homotopy fibrations in the middle and right column are exactly as defined in [Reference Theriault25, Corollary 3.14]. From this diagram, there is a homotopy equivalence ![]() $F_i \simeq H_i$, and as
$F_i \simeq H_i$, and as ![]() $\Sigma F_i \in {\mathcal{W}}$ we obtain
$\Sigma F_i \in {\mathcal{W}}$ we obtain ![]() $\Sigma H_i \in {\mathcal{W}}$. As all the conditions of Theorem 1.2 have been met, it follows that
$\Sigma H_i \in {\mathcal{W}}$. As all the conditions of Theorem 1.2 have been met, it follows that  ${(\underline{C\Omega X},\underline{\Omega X})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$.
${(\underline{C\Omega X},\underline{\Omega X})}^{{(\underline{K},\underline{L})}^{*M}} \in {\mathcal{P}}$.
7. The substitution complex and new examples
In this section, we show that the substitution operation can be used to generate new examples of simplicial complexes such that  $\Omega {(\underline{CA},\underline{A})}^{K} \in {\mathcal{P}}$. Recall that there are two known families of simplicial complexes where
$\Omega {(\underline{CA},\underline{A})}^{K} \in {\mathcal{P}}$. Recall that there are two known families of simplicial complexes where  $\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$: those
$\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$: those ![]() $K$ such that
$K$ such that  ${(\underline{CA},\underline{A})}^K \in {\mathcal{W}}$, and those
${(\underline{CA},\underline{A})}^K \in {\mathcal{W}}$, and those ![]() $K$ that are
$K$ that are ![]() $k$-skeletons of a flag complex. We wish to construct new examples of simplicial complexes where
$k$-skeletons of a flag complex. We wish to construct new examples of simplicial complexes where  $\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$ but
$\Omega {(\underline{CA},\underline{A})}^K \in {\mathcal{P}}$ but  ${(\underline{CA},\underline{A})}^K \notin {\mathcal{W}}$ and
${(\underline{CA},\underline{A})}^K \notin {\mathcal{W}}$ and ![]() $K$ is not the
$K$ is not the ![]() $k$-skeleton of a flag complex. To do this, we focus on the substitution complex, as we can determine some full subcomplexes in this case. We first give sufficient conditions to ensure that
$k$-skeleton of a flag complex. To do this, we focus on the substitution complex, as we can determine some full subcomplexes in this case. We first give sufficient conditions to ensure that  ${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)}$ is not in
${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)}$ is not in ![]() ${\mathcal{W}}$.
${\mathcal{W}}$.
Lemma 7.1. Let ![]() $K(K_1,\dots,K_m)$ be a substitution complex where at least one
$K(K_1,\dots,K_m)$ be a substitution complex where at least one ![]() $K_i$ is such that
$K_i$ is such that  ${(\underline{CA},\underline{A})}^{K_i} \notin {\mathcal{W}}$. Then
${(\underline{CA},\underline{A})}^{K_i} \notin {\mathcal{W}}$. Then  ${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \notin {\mathcal{W}}$.
${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \notin {\mathcal{W}}$.
Proof. Assume that  ${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \in {\mathcal{W}}$. By Corollary 3.11,
${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \in {\mathcal{W}}$. By Corollary 3.11, ![]() $K_i$ is a full subcomplex of
$K_i$ is a full subcomplex of ![]() $K(K_1,\dots,K_m)$. Therefore, by Lemma 2.10,
$K(K_1,\dots,K_m)$. Therefore, by Lemma 2.10, ${(\underline{CA},\underline{A})}^{K_i}$ retracts off
${(\underline{CA},\underline{A})}^{K_i}$ retracts off  ${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)}$. By Lemma 2.4, this implies that
${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)}$. By Lemma 2.4, this implies that  ${(\underline{CA},\underline{A})}^{K_i}$ has the homotopy type of a wedge of spheres, giving a contradiction. Therefore,
${(\underline{CA},\underline{A})}^{K_i}$ has the homotopy type of a wedge of spheres, giving a contradiction. Therefore,  ${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)}$ cannot have the homotopy type of a wedge of spheres.
${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)}$ cannot have the homotopy type of a wedge of spheres.
Lemma 7.2. Let ![]() $K(K_1,\dots,K_m)$ be a substitution complex and let
$K(K_1,\dots,K_m)$ be a substitution complex and let ![]() $K$ be such that
$K$ be such that  ${(\underline{CA},\underline{A})}^K \notin {\mathcal{W}}$. Then
${(\underline{CA},\underline{A})}^K \notin {\mathcal{W}}$. Then  ${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)}\notin {\mathcal{W}}$
${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)}\notin {\mathcal{W}}$
Proof. Assume that  ${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \in {\mathcal{W}}$. By Corollary 3.11, there is a copy of
${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \in {\mathcal{W}}$. By Corollary 3.11, there is a copy of ![]() $K$ contained in
$K$ contained in ![]() $K(K_1,\dots,K_m)$ which is a full subcomplex. Therefore, by Lemma 2.10, we have
$K(K_1,\dots,K_m)$ which is a full subcomplex. Therefore, by Lemma 2.10, we have  ${(\underline{CA},\underline{A})}^{K}$ retracting off
${(\underline{CA},\underline{A})}^{K}$ retracting off  ${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)}$. By Lemma 2.4, this implies that
${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)}$. By Lemma 2.4, this implies that  ${(\underline{CA},\underline{A})}^{K}$ has the homotopy type of a wedge of spheres, giving a contradiction. Therefore,
${(\underline{CA},\underline{A})}^{K}$ has the homotopy type of a wedge of spheres, giving a contradiction. Therefore,  ${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)}$ is not homotopy equivalent to a wedge of spheres, as
${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)}$ is not homotopy equivalent to a wedge of spheres, as  ${(\underline{CA},\underline{A})}^K \notin {\mathcal{W}}$.
${(\underline{CA},\underline{A})}^K \notin {\mathcal{W}}$.
We now wish to show that we can build substitution complexes that are not the ![]() $k$-skeletons of flag complexes. We first deal with the case where
$k$-skeletons of flag complexes. We first deal with the case where ![]() $K$ is not flag. Recall that a simplicial complex
$K$ is not flag. Recall that a simplicial complex ![]() $K$ is flag if every set of vertices of
$K$ is flag if every set of vertices of ![]() $K$ that are pairwise connected by edges form a face of
$K$ that are pairwise connected by edges form a face of ![]() $K$, and the
$K$, and the ![]() $k$-skeleton of a simplicial complex
$k$-skeleton of a simplicial complex ![]() $K$ is the collection of simplices of dimension
$K$ is the collection of simplices of dimension ![]() $k$ or less. A minimal missing face of
$k$ or less. A minimal missing face of ![]() $K$ is a subset
$K$ is a subset ![]() $\omega \subseteq [m]$ such that
$\omega \subseteq [m]$ such that ![]() $\omega \notin K$ but every proper subset of
$\omega \notin K$ but every proper subset of ![]() $\omega$ is a simplex in
$\omega$ is a simplex in ![]() $K$. We denote the set of missing faces of
$K$. We denote the set of missing faces of ![]() $K$ as
$K$ as ![]() $MF(K)$, and the set of minimal missing faces of
$MF(K)$, and the set of minimal missing faces of ![]() $K$ as
$K$ as ![]() $MMF(K)$. If
$MMF(K)$. If ![]() $K$ is a flag complex, its minimal missing faces are on no more than two vertices.
$K$ is a flag complex, its minimal missing faces are on no more than two vertices.
Lemma 7.3. ([Reference Abramyan and Panov1])
The minimal missing faces of ![]() $K(K_1,\dots,K_m)$ are precisely the following
$K(K_1,\dots,K_m)$ are precisely the following
 \begin{equation*}MMF(K_1) \sqcup \dots \sqcup MMF(K_m) \sqcup \bigsqcup_{\Delta(i_1,\dots,i_k)\in MMF(K)} MMF_{i_1,\dots,i_k}(K(K_1,\dots,K_m)) \end{equation*}
\begin{equation*}MMF(K_1) \sqcup \dots \sqcup MMF(K_m) \sqcup \bigsqcup_{\Delta(i_1,\dots,i_k)\in MMF(K)} MMF_{i_1,\dots,i_k}(K(K_1,\dots,K_m)) \end{equation*}where
Lemma 7.4. Let ![]() $K$ be a simplicial complex on the vertex set
$K$ be a simplicial complex on the vertex set ![]() $[m]$ that is not flag. Then the complex
$[m]$ that is not flag. Then the complex ![]() $K(K_1,\dots,K_m)$ is not flag.
$K(K_1,\dots,K_m)$ is not flag.
Proof. Relabelling vertices as required, let ![]() $\{1,\dots,k\}$,
$\{1,\dots,k\}$, ![]() $k \geq 2$ be a set of pairwise connected vertices that do not form a face of
$k \geq 2$ be a set of pairwise connected vertices that do not form a face of ![]() $K$. Let
$K$. Let ![]() $v_i$ denote a vertex in
$v_i$ denote a vertex in ![]() $K_i$, and consider the vertex set
$K_i$, and consider the vertex set ![]() $\{v_1,\dots,v_k\} \in K(K_1,\dots,K_m)$. This does not form a simplex in
$\{v_1,\dots,v_k\} \in K(K_1,\dots,K_m)$. This does not form a simplex in ![]() $K(K_1,\dots,K_m)$ as
$K(K_1,\dots,K_m)$ as ![]() $\{1,\dots,k\}$ is not a face of
$\{1,\dots,k\}$ is not a face of ![]() $K$. However, as each pair
$K$. However, as each pair ![]() $\{i,j\} \subseteq \{1,\dots,k\}$ is connected by an edge in
$\{i,j\} \subseteq \{1,\dots,k\}$ is connected by an edge in ![]() $K$, the pairs
$K$, the pairs ![]() $\{v_i,v_j\} \subseteq \{v_1,\dots,v_k\}$ are connected by an edge in
$\{v_i,v_j\} \subseteq \{v_1,\dots,v_k\}$ are connected by an edge in ![]() $K(K_1,\dots,K_m)$, and so the set
$K(K_1,\dots,K_m)$, and so the set ![]() $\{v_1,\dots,v_k\}$ is pairwise connected. Therefore, we have found a collection of pairwise connected vertices in
$\{v_1,\dots,v_k\}$ is pairwise connected. Therefore, we have found a collection of pairwise connected vertices in ![]() $K(K_1,\dots,K_m)$ that does not form a face, and so
$K(K_1,\dots,K_m)$ that does not form a face, and so ![]() $K(K_1,\dots,K_m)$ cannot be flag.
$K(K_1,\dots,K_m)$ cannot be flag.
Lemma 7.5. Let ![]() $K$ be a simplicial complex that is not flag. For at least one vertex
$K$ be a simplicial complex that is not flag. For at least one vertex ![]() $v$ in a minimal missing face of
$v$ in a minimal missing face of ![]() $K$, suppose that
$K$, suppose that ![]() $K_v$, that is, the simplicial complex substituted into
$K_v$, that is, the simplicial complex substituted into ![]() $K$ at vertex
$K$ at vertex ![]() $v$, contains a 1-simplex. Then
$v$, contains a 1-simplex. Then ![]() $K(K_1,\dots,K_m)$ is not the
$K(K_1,\dots,K_m)$ is not the ![]() $k$-skeleton of any flag complex.
$k$-skeleton of any flag complex.
Proof. As ![]() $K$ is not flag, it will have a minimal missing face on at least
$K$ is not flag, it will have a minimal missing face on at least ![]() $3$ vertices. Reordering vertices if necessary, let
$3$ vertices. Reordering vertices if necessary, let ![]() $\{1,\dots,j\}$ be a minimal missing face of
$\{1,\dots,j\}$ be a minimal missing face of ![]() $K$, and suppose that
$K$, and suppose that ![]() $K_j$ has at least one
$K_j$ has at least one ![]() $1$ simplex. By Lemma 7.3,
$1$ simplex. By Lemma 7.3, ![]() $\{v_1,\dots,v_j\}$ is a minimal missing face in
$\{v_1,\dots,v_j\}$ is a minimal missing face in ![]() $K(K_1,\dots,K_m)$, and as the boundary of
$K(K_1,\dots,K_m)$, and as the boundary of ![]() $(1,\dots,j)$ is contained in
$(1,\dots,j)$ is contained in ![]() $K$, the boundary of
$K$, the boundary of ![]() $(v_1,\dots,v_j)$ is contained in
$(v_1,\dots,v_j)$ is contained in ![]() $K(K_1,\dots,K_m)$. As
$K(K_1,\dots,K_m)$. As ![]() $\{v_1,\dots,v_j\}$ is a minimal missing face of
$\{v_1,\dots,v_j\}$ is a minimal missing face of ![]() $K(K_1,\dots,K_m)$, if
$K(K_1,\dots,K_m)$, if ![]() $K(K_1,\dots,K_m)$ was the
$K(K_1,\dots,K_m)$ was the ![]() $k$-skeleton of a flag complex, it could only be the
$k$-skeleton of a flag complex, it could only be the ![]() $j-1$-skeleton of a flag complex. Therefore, it could not contain any simplices of dimension greater than
$j-1$-skeleton of a flag complex. Therefore, it could not contain any simplices of dimension greater than ![]() $j-1$. Let
$j-1$. Let ![]() $v^1_j$ and
$v^1_j$ and ![]() $v^2_j$ denote two vertices of
$v^2_j$ denote two vertices of ![]() $K_j$ that are joined by an edge. The link of
$K_j$ that are joined by an edge. The link of ![]() $j$ in
$j$ in ![]() $K$ will contain the simplex
$K$ will contain the simplex ![]() $(1,\dots,j-2)$, and so by definition of the substitution operation, we have
$(1,\dots,j-2)$, and so by definition of the substitution operation, we have  $(v_1,\dots,v_{j-2},v^1_j,v^2_j) \in K(K_1,\dots,K_m)$, a contradiction. Therefore,
$(v_1,\dots,v_{j-2},v^1_j,v^2_j) \in K(K_1,\dots,K_m)$, a contradiction. Therefore, ![]() $K(K_1,\dots,K_m)$ cannot be the
$K(K_1,\dots,K_m)$ cannot be the ![]() $k$-skeleton of any flag complex.
$k$-skeleton of any flag complex.
We now consider the case when ![]() $K$ is flag.
$K$ is flag.
Lemma 7.6. Let ![]() $K$ be a flag complex on
$K$ be a flag complex on ![]() $[m]$ vertices. If at least one
$[m]$ vertices. If at least one ![]() $K_i$ substituted into
$K_i$ substituted into ![]() $K$ is not flag, then
$K$ is not flag, then ![]() $K(K_1,\dots,K_m)$ is not flag.
$K(K_1,\dots,K_m)$ is not flag.
Proof. By Lemma 7.3, all missing faces of each ![]() $K_i$ are missing faces of
$K_i$ are missing faces of ![]() $K(K_1,\dots,K_m)$. Therefore,
$K(K_1,\dots,K_m)$. Therefore, ![]() $K(K_1,\dots,K_m)$ will contain all the missing faces of
$K(K_1,\dots,K_m)$ will contain all the missing faces of ![]() $K_i$, and so cannot be flag.
$K_i$, and so cannot be flag.
Lemma 7.7. If ![]() $K$ is the
$K$ is the ![]() $k$-skeleton of a flag complex, and
$k$-skeleton of a flag complex, and ![]() $K \neq \Delta^k$, it must have a minimal missing face of dimension
$K \neq \Delta^k$, it must have a minimal missing face of dimension ![]() $k+1$.
$k+1$.
Proof. As ![]() $K$ is the
$K$ is the ![]() $k$-skeleton of a flag complex, it must have at least one face of dimension
$k$-skeleton of a flag complex, it must have at least one face of dimension ![]() $k$, and no higher faces. Let
$k$, and no higher faces. Let ![]() $K^f$ denote the minimal flag complex on the same 1-skeleton as
$K^f$ denote the minimal flag complex on the same 1-skeleton as ![]() $K$, so
$K$, so ![]() $K$ is the
$K$ is the ![]() $k$-skeleton of
$k$-skeleton of ![]() $K^f$. Up to a reordering of vertices, let
$K^f$. Up to a reordering of vertices, let ![]() $(1,\dots,k+2)$ be a
$(1,\dots,k+2)$ be a ![]() $(k+1)$-simplex of
$(k+1)$-simplex of ![]() $K^f$. In
$K^f$. In ![]() $K$, the set
$K$, the set ![]() $\{1,\dots,k+2\}$ does not form a simplex, as the dimension is greater than
$\{1,\dots,k+2\}$ does not form a simplex, as the dimension is greater than ![]() $k$, but the boundary is contained in
$k$, but the boundary is contained in ![]() $K$, because each
$K$, because each ![]() $k$ simplex in the boundary is in the
$k$ simplex in the boundary is in the ![]() $k$-skeleton of
$k$-skeleton of ![]() $K^f$, which is
$K^f$, which is ![]() $K$. Therefore,
$K$. Therefore, ![]() $\{1,\dots,k+2\}$ is a minimal missing face of
$\{1,\dots,k+2\}$ is a minimal missing face of ![]() $K$.
$K$.
Lemma 7.8. Let ![]() $K$ be a flag complex. If a) at least one
$K$ be a flag complex. If a) at least one ![]() $K_i$ is not the
$K_i$ is not the ![]() $k$-skeleton of a flag complex or b)
$k$-skeleton of a flag complex or b) ![]() $K_i$ is the
$K_i$ is the ![]() $k$-skeleton of a flag complex and the link of
$k$-skeleton of a flag complex and the link of ![]() $i$ in
$i$ in ![]() $K$ is non-empty, then
$K$ is non-empty, then ![]() $K(K_1,\dots,K_m)$ is not the
$K(K_1,\dots,K_m)$ is not the ![]() $k$-skeleton of a flag complex.
$k$-skeleton of a flag complex.
Proof. If at least one ![]() $K_i$ is not the
$K_i$ is not the ![]() $k$-skeleton of a flag complex, then by combining Lemma 7.3 and the argument from Lemma 7.6,
$k$-skeleton of a flag complex, then by combining Lemma 7.3 and the argument from Lemma 7.6, ![]() $K(K_1,\dots,K_m)$ cannot be the
$K(K_1,\dots,K_m)$ cannot be the ![]() $k$-skeleton of some flag complex. So now consider case b). As
$k$-skeleton of some flag complex. So now consider case b). As ![]() $K_i$ is the
$K_i$ is the ![]() $k$-skeleton of a flag complex, it will have a minimal missing face on at least
$k$-skeleton of a flag complex, it will have a minimal missing face on at least ![]() $k+2$ vertices, by Lemma 7.7. Reordering vertices if necessary, let
$k+2$ vertices, by Lemma 7.7. Reordering vertices if necessary, let ![]() $\{1,\dots,k+2\}$ be a minimal missing face of
$\{1,\dots,k+2\}$ be a minimal missing face of ![]() $K_i$. Therefore, if
$K_i$. Therefore, if ![]() $K(K_1,\dots,K_m)$ is the skeleton of a flag complex, it must be a
$K(K_1,\dots,K_m)$ is the skeleton of a flag complex, it must be a ![]() $k$-skeleton. By assumption, the link of
$k$-skeleton. By assumption, the link of ![]() $i$ is non-empty, and so there exists a
$i$ is non-empty, and so there exists a ![]() $\sigma$ such that
$\sigma$ such that ![]() $\sigma \cup \{i\} \in K$. By definition of substitution, for all
$\sigma \cup \{i\} \in K$. By definition of substitution, for all ![]() $\tau \in K_i$
$\tau \in K_i$ ![]() $\sigma \cup \tau \in K(K_1,\dots,K_m)$. More specifically, as the boundary of
$\sigma \cup \tau \in K(K_1,\dots,K_m)$. More specifically, as the boundary of ![]() $(1,\dots,k+2)$ is contained in
$(1,\dots,k+2)$ is contained in ![]() $K_i$,
$K_i$, ![]() $(1,\dots,k+1) \cup \sigma$ is a simplex in
$(1,\dots,k+1) \cup \sigma$ is a simplex in ![]() $K(K_1,\dots,K_m)$. But then we have a face of
$K(K_1,\dots,K_m)$. But then we have a face of ![]() $K(K_1,\dots,K_m)$ of a dimension that is strictly larger than
$K(K_1,\dots,K_m)$ of a dimension that is strictly larger than ![]() $k$, and so
$k$, and so ![]() $K(K_1,\dots,K_m)$ is not the
$K(K_1,\dots,K_m)$ is not the ![]() $k$-skeleton of a flag complex.
$k$-skeleton of a flag complex.
We end this section by building some substitution complexes such that  $\Omega {(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \in {\mathcal{P}}$, but
$\Omega {(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \in {\mathcal{P}}$, but  ${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \notin {\mathcal{W}}$ and
${(\underline{CA},\underline{A})}^{K(K_1,\dots,K_m)} \notin {\mathcal{W}}$ and ![]() $ K(K_1,\dots,K_m)$ is not the
$ K(K_1,\dots,K_m)$ is not the ![]() $k$-skeleton of a flag complex. We do this by substituting into the boundary of an
$k$-skeleton of a flag complex. We do this by substituting into the boundary of an ![]() $m$-simplex.
$m$-simplex.
Lemma 7.9. There are simplicial equivalences ![]() $(\partial\Delta^{l-1} \setminus \{l\})(K_{1},\dots,K_{l-1},l)$ and
$(\partial\Delta^{l-1} \setminus \{l\})(K_{1},\dots,K_{l-1},l)$ and ![]() $\Delta^{l-2}(K_1,\dots,K_{l-1})$ and
$\Delta^{l-2}(K_1,\dots,K_{l-1})$ and ![]() $\mathrm{lk}_{\partial\Delta^{l-1}(K_{1},\dots,K_{l-1},l)}(l)$ and
$\mathrm{lk}_{\partial\Delta^{l-1}(K_{1},\dots,K_{l-1},l)}(l)$ and ![]() $\partial \Delta^{l-2}(K_1,\dots,K_{l-1})$.
$\partial \Delta^{l-2}(K_1,\dots,K_{l-1})$.
Proof. These follows from Lemma 3.7, where ![]() ${(\underline{K},\underline{L})} = (\underline{K},\underline{\emptyset})$.
${(\underline{K},\underline{L})} = (\underline{K},\underline{\emptyset})$.
We now have all the ingredients in place to produce new examples of spaces in ![]() ${\mathcal{P}}$.
${\mathcal{P}}$.
Theorem 7.10. Let ![]() $\partial \Delta (K_1,\dots, K_n)$ be a substitution complex such that for each
$\partial \Delta (K_1,\dots, K_n)$ be a substitution complex such that for each ![]() $K_i$, we have
$K_i$, we have  $\Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{P}}$. Furthermore, suppose least one
$\Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{P}}$. Furthermore, suppose least one ![]() $K_i$ is such that
$K_i$ is such that  ${(\underline{CA},\underline{A})}^{K_i} \notin {\mathcal{W}}$. Then we have
${(\underline{CA},\underline{A})}^{K_i} \notin {\mathcal{W}}$. Then we have  ${(\underline{CA},\underline{A})}^{\partial \Delta (K_1,\dots, K_n)} \notin {\mathcal{W}}$,
${(\underline{CA},\underline{A})}^{\partial \Delta (K_1,\dots, K_n)} \notin {\mathcal{W}}$, ![]() $\partial \Delta(K_1,\dots,K_n)$ is not the
$\partial \Delta(K_1,\dots,K_n)$ is not the ![]() $k$-skeleton of a flag complex for any
$k$-skeleton of a flag complex for any ![]() $k$, and
$k$, and  $\Omega {(\underline{CA},\underline{A})}^{\partial \Delta (K_1,\dots, K_n)} \in {\mathcal{P}}$.
$\Omega {(\underline{CA},\underline{A})}^{\partial \Delta (K_1,\dots, K_n)} \in {\mathcal{P}}$.
Proof. As for all ![]() $i \in [m]$, we have
$i \in [m]$, we have  $\Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{P}}$, we obtain
$\Omega {(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{P}}$, we obtain  $\Omega {(\underline{CA},\underline{A})}^{\partial \Delta (K_1,\dots, K_n)} \in {\mathcal{P}}$ by Corollary 6.4. As there exists an
$\Omega {(\underline{CA},\underline{A})}^{\partial \Delta (K_1,\dots, K_n)} \in {\mathcal{P}}$ by Corollary 6.4. As there exists an ![]() $i$ such that
$i$ such that  ${(\underline{CA},\underline{A})}^{K_i} \notin {\mathcal{W}}$, by Lemma 7.1, we obtain that
${(\underline{CA},\underline{A})}^{K_i} \notin {\mathcal{W}}$, by Lemma 7.1, we obtain that  ${(\underline{CA},\underline{A})}^{\partial \Delta (K_1,\dots, K_n)} \notin {\mathcal{W}}$. As
${(\underline{CA},\underline{A})}^{\partial \Delta (K_1,\dots, K_n)} \notin {\mathcal{W}}$. As  ${(\underline{CA},\underline{A})}^{K_i} \notin {\mathcal{W}}$, we have that
${(\underline{CA},\underline{A})}^{K_i} \notin {\mathcal{W}}$, we have that ![]() $K_i$ must have at least one edge, as otherwise
$K_i$ must have at least one edge, as otherwise ![]() $K_i$ would be the disjoint union of points, and [Reference Grbić and Theriault15, Theorem 1] established that if
$K_i$ would be the disjoint union of points, and [Reference Grbić and Theriault15, Theorem 1] established that if ![]() $K_i$ is of this form, then
$K_i$ is of this form, then  ${(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{W}}$. As
${(\underline{CA},\underline{A})}^{K_i} \in {\mathcal{W}}$. As ![]() $\partial \Delta^{n-1}$ is not flag, Theorem 7.4 implies
$\partial \Delta^{n-1}$ is not flag, Theorem 7.4 implies ![]() $\partial \Delta (K_1,\dots, K_n)$ is not the
$\partial \Delta (K_1,\dots, K_n)$ is not the ![]() $k$-skeleton of a flag complex.
$k$-skeleton of a flag complex.
To conclude this section, we give a concrete example of a new complexe such that, the moment-angle complex ![]() ${\mathcal{Z}}_{K(K_1,\dots K_m)} \in {\mathcal{P}}$.
${\mathcal{Z}}_{K(K_1,\dots K_m)} \in {\mathcal{P}}$.
Example 7.11. Let ![]() $K = \partial \Delta^{n-1}$, and let each
$K = \partial \Delta^{n-1}$, and let each ![]() $K_i$ be the boundary of an
$K_i$ be the boundary of an ![]() $n_i$-gon, denoted
$n_i$-gon, denoted ![]() $P_{n_i}$, where
$P_{n_i}$, where ![]() $n_i \geq 4$. Observe that
$n_i \geq 4$. Observe that ![]() ${\mathcal{Z}}_{P_4} \simeq S^3 \times S^3$, and that for
${\mathcal{Z}}_{P_4} \simeq S^3 \times S^3$, and that for ![]() $m \gt 4$,by [Reference McGavran20, Theorem 3.4] we have
$m \gt 4$,by [Reference McGavran20, Theorem 3.4] we have  ${\mathcal{Z}}_{P_{n}} \cong \#_{k=3}^{n-1}(S^k \times S^{n+2-k})^{\#(k-2){n-1 \choose k-1}}$. Therefore, for
${\mathcal{Z}}_{P_{n}} \cong \#_{k=3}^{n-1}(S^k \times S^{n+2-k})^{\#(k-2){n-1 \choose k-1}}$. Therefore, for ![]() $n_i \geq 4$ we have that
$n_i \geq 4$ we have that ![]() ${\mathcal{Z}}_{P_{n_i}} \notin {\mathcal{W}}$. As
${\mathcal{Z}}_{P_{n_i}} \notin {\mathcal{W}}$. As ![]() $\Omega {\mathcal{Z}}_{P_n} \simeq \Omega S^3 \times \Omega S^{n-1} \times \Omega S(P_n)$ [Reference Beben and Theriault9, Theorem 1.4], where
$\Omega {\mathcal{Z}}_{P_n} \simeq \Omega S^3 \times \Omega S^{n-1} \times \Omega S(P_n)$ [Reference Beben and Theriault9, Theorem 1.4], where ![]() $S(P_n)$ is a wedge of simply connected spheres, we have
$S(P_n)$ is a wedge of simply connected spheres, we have ![]() $\Omega {\mathcal{Z}}_{P_n} \in {\mathcal{P}}$. By Theorem 7.10,
$\Omega {\mathcal{Z}}_{P_n} \in {\mathcal{P}}$. By Theorem 7.10, ![]() ${\mathcal{Z}}_{\partial \Delta^{m-1}(P_{n_1},\dots,P_{n_m})} \in {\mathcal{P}}$.
${\mathcal{Z}}_{\partial \Delta^{m-1}(P_{n_1},\dots,P_{n_m})} \in {\mathcal{P}}$.
Acknowledgements
The author would like to thank Stephen Theriault for many valuable and constructive discussions during the preparation of this work. The author would also like to thank Lewis Stanton for reading a draft of this work and providing insightful comments.



