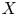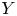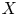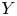Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Munro, Zachary
2023.
A note on abelian cubulated groups.
Bulletin of the London Mathematical Society,
Vol. 55,
Issue. 5,
p.
2277.
Genevois, Anthony
Lonjou, Anne
and
Urech, Christian
2024.
Cremona Groups Over Finite Fields, Neretin Groups, and Non-Positively Curved Cube Complexes.
International Mathematics Research Notices,
Vol. 2024,
Issue. 1,
p.
554.