1. Introduction
Obstructions to the existence of open books are found in all dimensions and are known to be complete in all dimensions except 4 [Reference Quinn25]. Kirby calculus is a successful approach to studying 4-dimensional manifolds [Reference Gompf and Stipsicz10], which we would like to apply to study open books in dimension 4.
We introduce the notion of a half open book, a generalization of a ‘lens thickening’ [Reference Baader and Graf2], whose Kirby diagram is well known. Our Algorithm 4.4 for constructing a Kirby diagram of an open book simply involves adding a framed link to a Kirby diagram of a half open book, which corresponds to gluing two half open books together (Figure 1). This will quickly yield Theorem 7.2, where we show that an open book constructed with an arbitrary page and a trivial monodromy can be alternatively constructed using a simple page, namely, a punctured handlebody, and a simple but nontrivial monodromy composed of sphere twists and torus twists. A handlebody is a 3-manifold with boundary obtained from D 3 by attaching 1-handles, and by a punctured handlebody, we mean a handlebody with open 3-balls removed from its interior. Finally, we prove that the diffeomorphism type of the spin of a lens space ![]() $\operatorname{L}(p,q)$ is independent of q, a result due to [Reference Meier18, Reference Pao22, Reference Plotnick23], using Kirby calculus. Section 5 is dedicated to examples that effectively capture the main ideas.
$\operatorname{L}(p,q)$ is independent of q, a result due to [Reference Meier18, Reference Pao22, Reference Plotnick23], using Kirby calculus. Section 5 is dedicated to examples that effectively capture the main ideas.
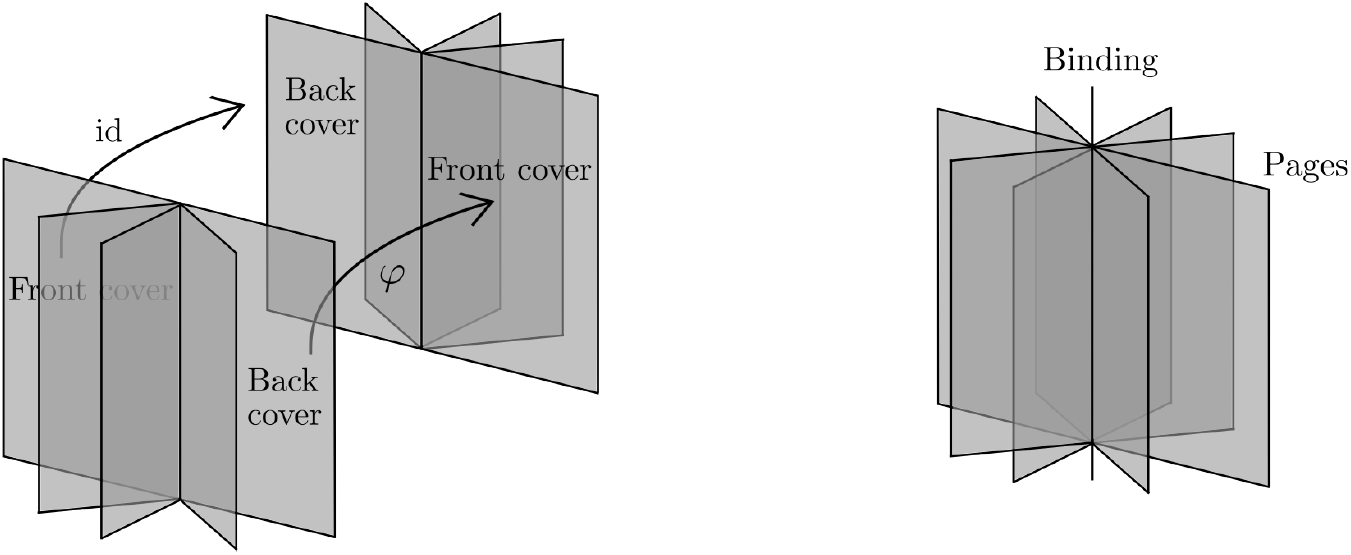
Figure 1. Gluing two half open books gives an open book.
We start by recalling the definitions necessary to state our main results. Given a compact oriented 3-manifold M with a non-empty boundary called a page and a self-diffeomorphism ![]() $\varphi\colon M\rightarrow M$ that restricts to the identity map in a neighbourhood of
$\varphi\colon M\rightarrow M$ that restricts to the identity map in a neighbourhood of ![]() $\partial M$ called the monodromy, the open book
$\partial M$ called the monodromy, the open book ![]() $\operatorname{Ob}(M,\varphi)$ is diffeomorphic to the closed 4-manifold
$\operatorname{Ob}(M,\varphi)$ is diffeomorphic to the closed 4-manifold ![]() $M\times [0,1]/\sim_\varphi$, where the equivalence relation isgiven by
$M\times [0,1]/\sim_\varphi$, where the equivalence relation isgiven by
Theorem 7.2. Given any compact oriented 3-manifold M with a non-empty boundary, there exists a monodromy φ on a punctured handlebody H such that ![]() $\operatorname{Ob}(H,\varphi)$is diffeomorphic to
$\operatorname{Ob}(H,\varphi)$is diffeomorphic to ![]() $\operatorname{Ob}(M,\operatorname{id})$.
$\operatorname{Ob}(M,\operatorname{id})$.
A Heegaard diagram is a way of presenting a 3-manifold with non-empty boundary in ![]() $\mathbb{R}^2$. We think of
$\mathbb{R}^2$. We think of ![]() $\mathbb{R}^2$ as the boundary of the 0-handle
$\mathbb{R}^2$ as the boundary of the 0-handle ![]() $\partial D^3=S^2$ with a single point removed to which we attach 1- and 2-handles. The attaching region of a 1-handle is indicated with a pair of D 2’s and the attaching sphere of a 2-handle is represented by a simple closed curve as in Figure 2. Similarly, one can regard
$\partial D^3=S^2$ with a single point removed to which we attach 1- and 2-handles. The attaching region of a 1-handle is indicated with a pair of D 2’s and the attaching sphere of a 2-handle is represented by a simple closed curve as in Figure 2. Similarly, one can regard ![]() $\mathbb{R}^3$ as the boundary of the 4-dimensional 0-handle with a point removed. In the 4-dimensional case, the attaching region of a 1-handle is specified by a pair of D 3’s. In addition to marking the attaching sphere, the framing of a 2-handle also needs to be specified. A parallel curve of the attaching sphere of a 2-handle can be used to encode a trivialization of its tubular neighborhood in
$\mathbb{R}^3$ as the boundary of the 4-dimensional 0-handle with a point removed. In the 4-dimensional case, the attaching region of a 1-handle is specified by a pair of D 3’s. In addition to marking the attaching sphere, the framing of a 2-handle also needs to be specified. A parallel curve of the attaching sphere of a 2-handle can be used to encode a trivialization of its tubular neighborhood in ![]() $\mathbb{R}^3$. As a consequence of [Reference Laudenbach and Poénaru16], there is essentially a unique way to obtain a closed 4-manifold by attaching 3- and 4-handles. Hence such a diagram, called a Kirby diagram, defines a closed 4-manifold up to diffeomorphism. A closed 4-manifold has no unique Kirby diagram, handle pair creation/cancellation, and handle sliding form a complete set of moves that allows one to go from one diagram to another of the same manifold [Reference Cerf4]. For an exposition of Kirby diagrams and Heegaard diagrams the reader is referred to the book [Reference Gompf and Stipsicz10] by Gompf and Stipsicz.
$\mathbb{R}^3$. As a consequence of [Reference Laudenbach and Poénaru16], there is essentially a unique way to obtain a closed 4-manifold by attaching 3- and 4-handles. Hence such a diagram, called a Kirby diagram, defines a closed 4-manifold up to diffeomorphism. A closed 4-manifold has no unique Kirby diagram, handle pair creation/cancellation, and handle sliding form a complete set of moves that allows one to go from one diagram to another of the same manifold [Reference Cerf4]. For an exposition of Kirby diagrams and Heegaard diagrams the reader is referred to the book [Reference Gompf and Stipsicz10] by Gompf and Stipsicz.
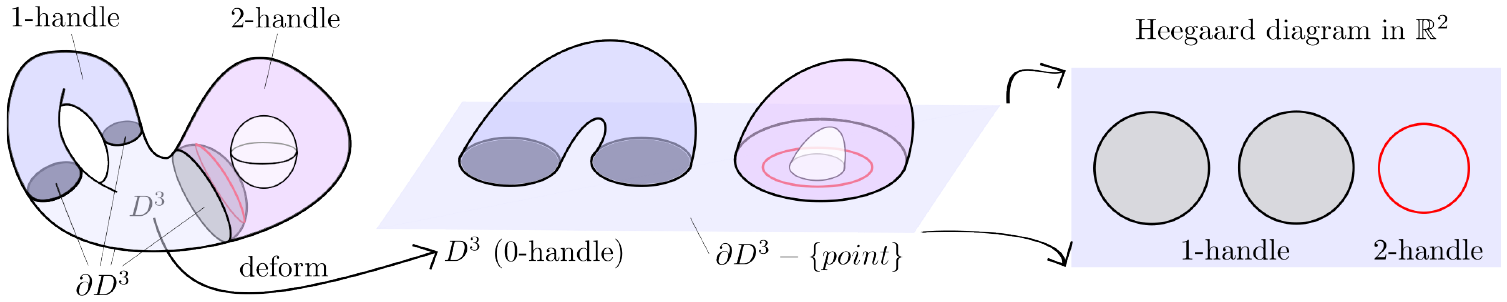
Figure 2. Handle decomposition to the Heegaard diagram (of the punctured solid torus).
Algorithm 4.4.
Given a Heegaard diagram of M and the image under φ of each 2-handle in M, one obtains a Kirby diagram of the open book ![]() $\operatorname{Ob}(M,\varphi)$ by applying the following algorithm:
$\operatorname{Ob}(M,\varphi)$ by applying the following algorithm:
(1) Replace every 1-handle attaching region with a pair of D3s.
(2) Add blackboard framing to every 2-handle attaching sphere.
(3) Add behind the blackboard plane a half-meridian with blackboard framing to each 2-handle attaching sphere.
(4) Add in front of the blackboard plane a half-meridian with blackboard framing to each 2-handle attaching sphere and then replace them with their images under the monodromy φ.
The result of step 2 is a Kirby diagram of a half open book, see Algorithm 4.1. To place the image under φ of the 2-handles into the Kirby diagram of the half open book, we identify each half-space in ![]() $\mathbb{R}^3$ separated by the blackboard with the page manifold, which will be explained in Proposition 4.3.
$\mathbb{R}^3$ separated by the blackboard with the page manifold, which will be explained in Proposition 4.3.
In Figure 3, the Kirby diagram obtained using Algorithm 4.4, with page punctured solid torus and monodromy torus twist (Defintion 6.2) as input, consists of a 1-handle whose belt sphere intersects the attaching sphere of a 2-handle and another 2-handle whose belt sphere intersects the attaching sphere of a 3-handle. Handle cancellation results in a blank diagram, a Kirby diagram of S 4, where a single 4-handle is glued to the 0-handle. This implies that ![]() $\operatorname{Ob}(M',\varphi')$ is diffeomorphic to
$\operatorname{Ob}(M',\varphi')$ is diffeomorphic to ![]() $\operatorname{Ob}(M,\varphi)\#S^4$, where M ʹ is obtained from M by taking a connected sum with a punctured solid torus and
$\operatorname{Ob}(M,\varphi)\#S^4$, where M ʹ is obtained from M by taking a connected sum with a punctured solid torus and ![]() $\varphi'$ is the composition of φ with a trivial extension of a torus twist. In particular, Figure 3 exhibits a 4-dimensional open book stabilization as mentioned in [Reference Kegel and Schmäschke14].
$\varphi'$ is the composition of φ with a trivial extension of a torus twist. In particular, Figure 3 exhibits a 4-dimensional open book stabilization as mentioned in [Reference Kegel and Schmäschke14].
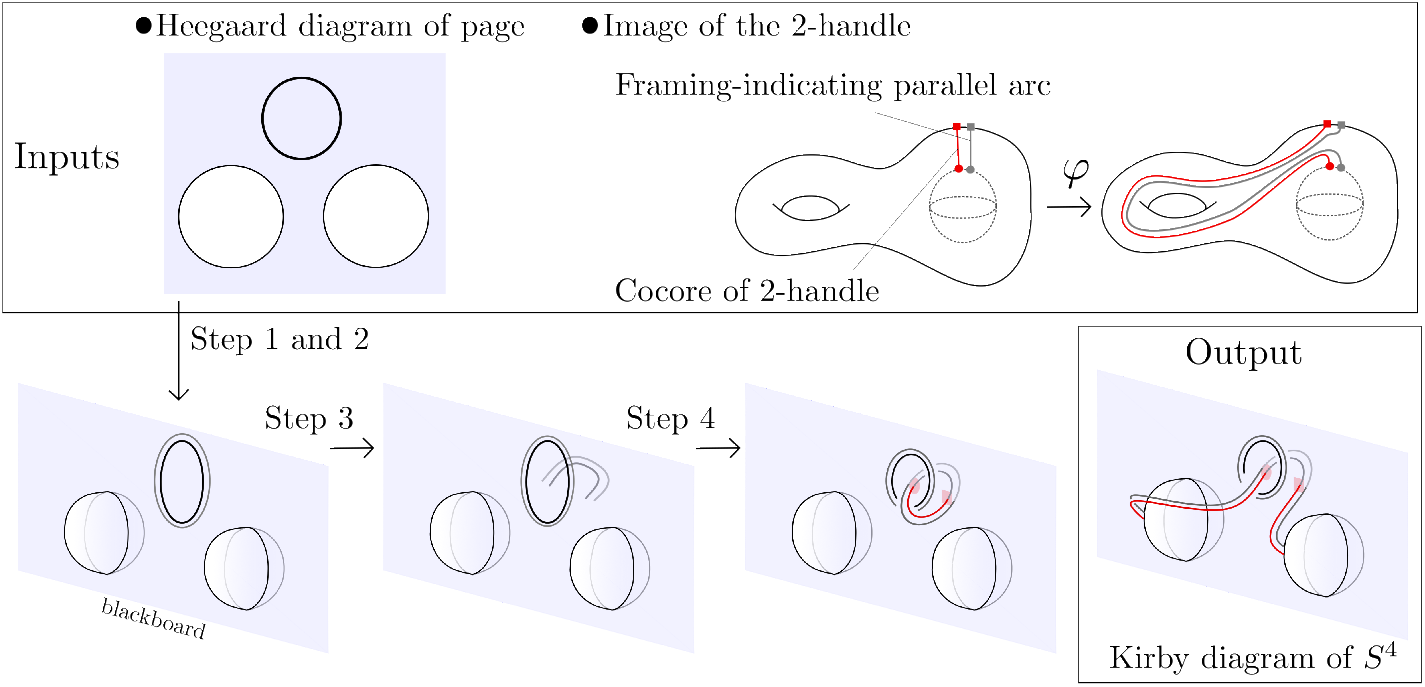
Figure 3. Algorithm 4.4.
Kirby diagrams of spun 4-manifolds, which are open books with binding S 2, are constructed in [Reference Montesinos20]. An algorithm to obtain a trisection from a Kirby diagram is presented in [Reference Kepplinger15]. For a practical algorithm obtaining a trisection diagram from a 4-dimensional open book, see [Reference Kegel and Schmäschke14].
1.1. Convention
Throughout this paper, all maps are smooth and all manifolds are compact, oriented, connected and smooth. There is a preferred way to smooth corners [Reference Gompf and Stipsicz10, Remark 1.3.3], and hence we do distinguish between manifolds with and without corners. Concerning handle decomposition of 3-manifolds with a non-empty boundary, we always assume that there are a unique 0-handle and no 3-handles [Reference Gompf and Stipsicz10, p. 112] and that handles are attached in order of non-decreasing indices to the boundary of handles of lower indices.
2. Background
An open book is a geometric structure that arises naturally from many fields of mathematics. The application of open books includes the study of fibered knots [Reference Alexander1], zero sets of complex polynomials [Reference Milnor19], spun embeddings [Reference Pancholi, Pandit and Saha21] and contact structures [Reference Giroux8], just to name a few.
An open book decomposition ![]() $(B,\pi)$ of a closed n-manifold X consists of a binding B and a fibration
$(B,\pi)$ of a closed n-manifold X consists of a binding B and a fibration ![]() $\pi\colon X\backslash B\rightarrow S^1$. The binding is a non-empty, not necessarily connected, codimension two submanifold of X a with trivial normal bundle. On a neighbourhood
$\pi\colon X\backslash B\rightarrow S^1$. The binding is a non-empty, not necessarily connected, codimension two submanifold of X a with trivial normal bundle. On a neighbourhood ![]() $N(B)\subset X$ of B, there exists a trivialization
$N(B)\subset X$ of B, there exists a trivialization ![]() $N(B)\approx B\times D^2$ using polar coordinates
$N(B)\approx B\times D^2$ using polar coordinates ![]() $(r,\phi)$ on D 2, such that
$(r,\phi)$ on D 2, such that ![]() $\pi|_{N(B)\backslash B}=\phi$. For each
$\pi|_{N(B)\backslash B}=\phi$. For each ![]() $t\in S^1$, the preimage
$t\in S^1$, the preimage ![]() $\pi^{-1}(t)$ is called a fibre and its compactification
$\pi^{-1}(t)$ is called a fibre and its compactification ![]() $\overline{\pi^{-1}(t)}$ is called a page of the open book.
$\overline{\pi^{-1}(t)}$ is called a page of the open book.
An abstract open book decomposition ![]() $(M,\varphi)$ of a closed n-manifold X consists of a page M and a monodromy φ. The page is a compact
$(M,\varphi)$ of a closed n-manifold X consists of a page M and a monodromy φ. The page is a compact ![]() $(n-1)$-manifold M with a non-empty boundary, and the monodromy is an orientation-preserving self-diffeomorphism on M that equals the identity map in a neighbourhood of the boundary
$(n-1)$-manifold M with a non-empty boundary, and the monodromy is an orientation-preserving self-diffeomorphism on M that equals the identity map in a neighbourhood of the boundary ![]() $\partial M$. X is diffeomorphic to the closed n-manifold
$\partial M$. X is diffeomorphic to the closed n-manifold
denoted by ![]() $\operatorname{Ob}(M,\varphi)$, where the equivalence relation is given by
$\operatorname{Ob}(M,\varphi)$, where the equivalence relation is given by
An abstract open book decomposition ![]() $(M,\varphi)$ gives rise to an open book decomposition whose binding is
$(M,\varphi)$ gives rise to an open book decomposition whose binding is  $\partial M\times [0,\frac{1}{2}]/\sim_{\varphi}$ and whose pages are
$\partial M\times [0,\frac{1}{2}]/\sim_{\varphi}$ and whose pages are ![]() $M\times\{t\}$. Since Kirby diagrams are defined up to diffeomorphism, we do not need to distinguish between abstract and non-abstract open book decompositions. More details can be found in [Reference Colin, Presas and Vogel5] and [Reference Etnyre7, Remark 2.6].
$M\times\{t\}$. Since Kirby diagrams are defined up to diffeomorphism, we do not need to distinguish between abstract and non-abstract open book decompositions. More details can be found in [Reference Colin, Presas and Vogel5] and [Reference Etnyre7, Remark 2.6].
In dimension 3, every closed manifold has open book decompositions [Reference Alexander1]. All closed, simply connected manifolds of dimension ![]() $\geq 6$ with vanishing signature admit open book decompositions [Reference Winkelnkemper28], and all closed manifolds of odd dimension
$\geq 6$ with vanishing signature admit open book decompositions [Reference Winkelnkemper28], and all closed manifolds of odd dimension ![]() $\geq 7$ admit open book decompositions [Reference Lawson17]. Quinn proved the state-of-the-art theorem of open books showing that an n-manifold admits an open book decomposition if and only if its signature and its Quinn-invariant vanish, where n ≠ 4 [Reference Quinn25]. The Quinn invariant, also called the asymmetric signature, of a simply connected manifold vanishes if and only if the usual signature does. It is extracted from a version of a middle-dimensional intersection form with group ring coefficients and takes values in a certain Witt group of such forms. This obstruction class vanishes if and only if the corresponding form admits stably a Lagrangian. For further details on this, we refer to the original works [Reference Quinn25, Reference Ranicki26]. It remains unknown whether these obstructions are complete for the case n = 4. Thus, we would like to initiate a study of 4-dimensional open books using a tool exclusive to dimension 4 – Kirby diagrams.
$\geq 7$ admit open book decompositions [Reference Lawson17]. Quinn proved the state-of-the-art theorem of open books showing that an n-manifold admits an open book decomposition if and only if its signature and its Quinn-invariant vanish, where n ≠ 4 [Reference Quinn25]. The Quinn invariant, also called the asymmetric signature, of a simply connected manifold vanishes if and only if the usual signature does. It is extracted from a version of a middle-dimensional intersection form with group ring coefficients and takes values in a certain Witt group of such forms. This obstruction class vanishes if and only if the corresponding form admits stably a Lagrangian. For further details on this, we refer to the original works [Reference Quinn25, Reference Ranicki26]. It remains unknown whether these obstructions are complete for the case n = 4. Thus, we would like to initiate a study of 4-dimensional open books using a tool exclusive to dimension 4 – Kirby diagrams.
3. Kirby diagrams of half open books
An open book is given by two copies of half open books glued together. Thus, a Kirby diagram of an open book with page M can be obtained from a Kirby diagram of a half open book, with the same page, by adding a framed link. The main goal of this section is to present Algorithm 3.7 for constructing a Kirby diagram of half open books. We begin by introducing our non-standard definitions.
Let M be a compact ![]() $(n-1)$-manifold with a non-empty boundary.
$(n-1)$-manifold with a non-empty boundary.
Definition 3.1. The half open book with page M is the n-manifold  $M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$, where the equivalence relation is given by
$M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$, where the equivalence relation is given by
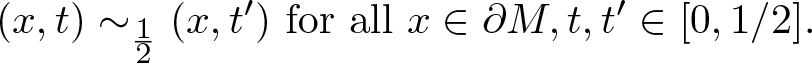 \begin{equation*}(x,t)\sim_\frac{1}{2}(x,t') \text{ for all } x\in \partial M, t,t'\in [0,1/2].\end{equation*}
\begin{equation*}(x,t)\sim_\frac{1}{2}(x,t') \text{ for all } x\in \partial M, t,t'\in [0,1/2].\end{equation*} Call ![]() $M\times \{0\}$ and
$M\times \{0\}$ and  $M\times \{\frac{1}{2}\}\subset \partial(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$ the front and back cover of the half open book, respectively. The codimension two submanifold
$M\times \{\frac{1}{2}\}\subset \partial(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$ the front and back cover of the half open book, respectively. The codimension two submanifold ![]() $\partial M$ of the half open book is called the binding.
$\partial M$ of the half open book is called the binding.
The double of an n-manifold N with a non-empty boundary, denoted by DN, is an n-manifold without boundary obtained from N by gluing −N to it along the boundary using the identity map on ![]() $\partial N$. The boundary of the half open book with page M, which consists of the front and back cover glued along the binding, is diffeomorphic to DM.
$\partial N$. The boundary of the half open book with page M, which consists of the front and back cover glued along the binding, is diffeomorphic to DM.
Definition 3.2. Given a monodromy ![]() $\varphi\colon M\rightarrow M$, we glue two half open books with page M with φ as follows:
$\varphi\colon M\rightarrow M$, we glue two half open books with page M with φ as follows:
• glue the front cover of the second copy to the back cover of the first copy using the identity map
 $\operatorname{id}$ and
$\operatorname{id}$ and• glue the back cover of the second copy to the front cover of the first copy using the monodromy map φ.
Let  $D_{\varphi}(M\times[0,\frac{1}{2}]/\sim_{\frac{1}{2}})$ denote the result of gluing two half open books with page M with φ.
$D_{\varphi}(M\times[0,\frac{1}{2}]/\sim_{\frac{1}{2}})$ denote the result of gluing two half open books with page M with φ.
Remark 3.3. Definition 3.2 is well-defined since a monodromy map is equal to the identity map in a neighbourhood of ![]() $\partial M$. The result of gluing two half open books
$\partial M$. The result of gluing two half open books  $D_{\operatorname{id}}(M\times[0,\frac{1}{2}]/\sim_{\frac{1}{2}})$ with the identity map is the double
$D_{\operatorname{id}}(M\times[0,\frac{1}{2}]/\sim_{\frac{1}{2}})$ with the identity map is the double  $D(M\times[0,\frac{1}{2}]/\sim_{\frac{1}{2}})$ of the half open book. This explains our choice of notation.
$D(M\times[0,\frac{1}{2}]/\sim_{\frac{1}{2}})$ of the half open book. This explains our choice of notation.
Proposition 3.4. The result of gluing two half open books is an open book; more explicitly,  $D_{\varphi}(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$ is diffeomorphic to
$D_{\varphi}(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$ is diffeomorphic to ![]() $\operatorname{Ob}(M,\varphi)$.
$\operatorname{Ob}(M,\varphi)$.
Proof. The proof follows by definition. Gluing to the back cover of  $M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$ the front cover of
$M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$ the front cover of  $M\times [\frac{1}{2},1]/\sim_\frac{1}{2}$ with the identity map, we get
$M\times [\frac{1}{2},1]/\sim_\frac{1}{2}$ with the identity map, we get ![]() $M\times [0,1]/\sim$, where
$M\times [0,1]/\sim$, where ![]() $(x,t)\sim(x,t')\text{ for all } x\in \partial M, t,t'\in [0,1]$. Gluing the back cover of
$(x,t)\sim(x,t')\text{ for all } x\in \partial M, t,t'\in [0,1]$. Gluing the back cover of  $M\times [\frac{1}{2},1]/\sim_\frac{1}{2}$ to the front cover of
$M\times [\frac{1}{2},1]/\sim_\frac{1}{2}$ to the front cover of  $M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$ using φ is equivalent to identifying
$M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$ using φ is equivalent to identifying ![]() $(x,1)$ with
$(x,1)$ with ![]() $(\varphi(x),0)$ for all
$(\varphi(x),0)$ for all ![]() $(x,1)\in M\times [0,1]/\sim$, which gives
$(x,1)\in M\times [0,1]/\sim$, which gives ![]() $\operatorname{Ob}(M,\varphi)$.
$\operatorname{Ob}(M,\varphi)$.
Example 3.5. The half open book with page ![]() $[0,1]$ is given by identifying
$[0,1]$ is given by identifying  $(0,0)\in [0,1]\times [0,\frac{1}{2}]$ with
$(0,0)\in [0,1]\times [0,\frac{1}{2}]$ with ![]() $(0,t)$ for all
$(0,t)$ for all  $t\in[0,\frac{1}{2}]$ and identifying
$t\in[0,\frac{1}{2}]$ and identifying ![]() $(1,0)$ with
$(1,0)$ with ![]() $(1,t)$ for all
$(1,t)$ for all  $t\in[0,\frac{1}{2}]$. It is diffeomorphic to D 2, and its boundary, the double of
$t\in[0,\frac{1}{2}]$. It is diffeomorphic to D 2, and its boundary, the double of ![]() $[0,1]$, is diffeomorphic to S 1. By Proposition 3.4, the open book
$[0,1]$, is diffeomorphic to S 1. By Proposition 3.4, the open book ![]() $\operatorname{Ob}([0,1],\operatorname{id})$ is diffeomorphic to
$\operatorname{Ob}([0,1],\operatorname{id})$ is diffeomorphic to ![]() $D(D^2)=S^2$.
$D(D^2)=S^2$.
Proposition 3.6. A handle decomposition of an ![]() $(n-1)$-dimensional manifold M induces a handle decomposition of the n-dimensional half open book
$(n-1)$-dimensional manifold M induces a handle decomposition of the n-dimensional half open book  $M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$.
$M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$.
Proof. Firstly, we construct a handle decomposition of  $M\times [0,\frac{1}{2}]$ from a handle decomposition of M. Suppose M is diffeomorphic to the result
$M\times [0,\frac{1}{2}]$ from a handle decomposition of M. Suppose M is diffeomorphic to the result
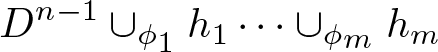 \begin{equation*}D^{n-1}\cup_{\phi_1} h_1 \dots\cup_{\phi_m} h_m\end{equation*}
\begin{equation*}D^{n-1}\cup_{\phi_1} h_1 \dots\cup_{\phi_m} h_m\end{equation*} of attaching the handle hi via the attaching map ϕi to ![]() $\partial D^{n-1}$ for
$\partial D^{n-1}$ for ![]() $i=1,\dots,m$. Here, the subscript i is not the index of the handle but an enumeration. To begin with, the
$i=1,\dots,m$. Here, the subscript i is not the index of the handle but an enumeration. To begin with, the ![]() $(n-1)$-dimensional 0-handle
$(n-1)$-dimensional 0-handle ![]() $D^{n-1}$ of M induces an n-dimensional 0-handle of
$D^{n-1}$ of M induces an n-dimensional 0-handle of  $M\times[0,\frac{1}{2}]$. Now, assume that the first i handles of M have induced i-many handles of
$M\times[0,\frac{1}{2}]$. Now, assume that the first i handles of M have induced i-many handles of  $M\times[0,\frac{1}{2}]$, i.e. assume we have obtained a handle decomposition of
$M\times[0,\frac{1}{2}]$, i.e. assume we have obtained a handle decomposition of  $M_{i-1}\times [0,\frac{1}{2}]$, where
$M_{i-1}\times [0,\frac{1}{2}]$, where  $M_{i-1}=D^{n-1}\cup_{\varphi_1}h_1\dots\cup_{\phi_{i-1}}h_{i-1}$ and
$M_{i-1}=D^{n-1}\cup_{\varphi_1}h_1\dots\cup_{\phi_{i-1}}h_{i-1}$ and ![]() $0 \lt i-1 \lt m$. Let
$0 \lt i-1 \lt m$. Let ![]() $\phi_i\colon \partial D^k\times D^{(n-1)-k}\rightarrow \partial M_{i-1}$ be the attaching map of an
$\phi_i\colon \partial D^k\times D^{(n-1)-k}\rightarrow \partial M_{i-1}$ be the attaching map of an ![]() $(n-1)$-dimensional k-handle hi. Then, it induces an n-dimensional k-handle
$(n-1)$-dimensional k-handle hi. Then, it induces an n-dimensional k-handle ![]() $h_i'$ of
$h_i'$ of  $M\times [0,\frac{1}{2}]$ with attaching map
$M\times [0,\frac{1}{2}]$ with attaching map
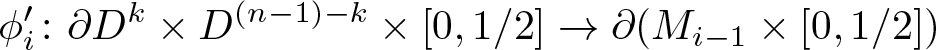 \begin{equation*}\phi_i'\colon\partial D^k\times D^{(n-1)-k}\times [0,1/2]\rightarrow \partial(M_{i-1}\times [0,1/2])\end{equation*}
\begin{equation*}\phi_i'\colon\partial D^k\times D^{(n-1)-k}\times [0,1/2]\rightarrow \partial(M_{i-1}\times [0,1/2])\end{equation*}given componentwise by
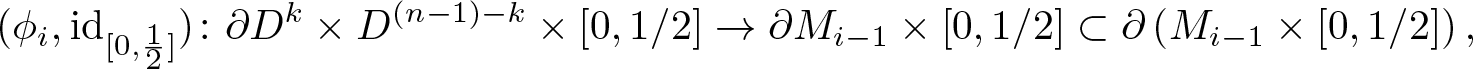 \begin{equation*} (\phi_i,\operatorname{id}_{[0,\frac{1}{2}]})\colon\partial D^k\times D^{(n-1)-k}\times [0,1/2]\rightarrow\partial M_{i-1}\times [0,1/2]\subset \partial\left(M_{i-1}\times [0,1/2]\right),\end{equation*}
\begin{equation*} (\phi_i,\operatorname{id}_{[0,\frac{1}{2}]})\colon\partial D^k\times D^{(n-1)-k}\times [0,1/2]\rightarrow\partial M_{i-1}\times [0,1/2]\subset \partial\left(M_{i-1}\times [0,1/2]\right),\end{equation*} such that  $M_i\times[0,\frac{1}{2}]$ is diffeomorphic to
$M_i\times[0,\frac{1}{2}]$ is diffeomorphic to  $(M_{i-1}\times [0,\frac{1}{2}]) \cup_{\phi_i'}h_i'$. Note that
$(M_{i-1}\times [0,\frac{1}{2}]) \cup_{\phi_i'}h_i'$. Note that  $D^{(n-1)-k}\times [0,\frac{1}{2}]$ is diffeomorphic to
$D^{(n-1)-k}\times [0,\frac{1}{2}]$ is diffeomorphic to ![]() $D^{n-k}$. By induction, we obtain a handle decomposition of
$D^{n-k}$. By induction, we obtain a handle decomposition of  $M\times[0,\frac{1}{2}]$.
$M\times[0,\frac{1}{2}]$.
Secondly, we show that ![]() $\sim_{\frac{1}{2}}$ preserves the handle decomposition, i.e. the handle decomposition on
$\sim_{\frac{1}{2}}$ preserves the handle decomposition, i.e. the handle decomposition on  $M\times [0,\frac{1}{2}]$ induces a handle decomposition on
$M\times [0,\frac{1}{2}]$ induces a handle decomposition on  $M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$. Let us look closely at some k-handle
$M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$. Let us look closely at some k-handle ![]() $h_i'$ in
$h_i'$ in  $M\times [0,\frac{1}{2}]$. If
$M\times [0,\frac{1}{2}]$. If  $\phi_i'(\partial D^k \times D^{(n-1)-k}\times [0,\frac{1}{2}])\cap \partial (M\times [0,\frac{1}{2}])=\emptyset$, then no identification will take place on this handle. Then, by using the identification
$\phi_i'(\partial D^k \times D^{(n-1)-k}\times [0,\frac{1}{2}])\cap \partial (M\times [0,\frac{1}{2}])=\emptyset$, then no identification will take place on this handle. Then, by using the identification  $D^{(n-1)-k}\times [0,\frac{1}{2}]\approx D^{n-k}$,
$D^{(n-1)-k}\times [0,\frac{1}{2}]\approx D^{n-k}$, ![]() $\phi_i'$ can be seen as an attaching map of an induced n-dimensional k-handle in
$\phi_i'$ can be seen as an attaching map of an induced n-dimensional k-handle in  $(M\times [0,\frac{1}{2}])/\sim_\frac{1}{2}$ and we are done. The points
$(M\times [0,\frac{1}{2}])/\sim_\frac{1}{2}$ and we are done. The points  $\phi_i'(\partial D^k \times \operatorname{int}(D^{(n-1)-k})\times [0,\frac{1}{2}])\subset \operatorname{int}(M)\times [0,\frac{1}{2}]$ always remain distinct points in the quotient of
$\phi_i'(\partial D^k \times \operatorname{int}(D^{(n-1)-k})\times [0,\frac{1}{2}])\subset \operatorname{int}(M)\times [0,\frac{1}{2}]$ always remain distinct points in the quotient of ![]() $\sim_{\frac{1}{2}}$. Hence, if
$\sim_{\frac{1}{2}}$. Hence, if  $\phi_i'((\partial D^k)\times D^{(n-1)-k}\times [0,\frac{1}{2}])\cap \partial (M\times [0,\frac{1}{2}]) \neq\emptyset$, then
$\phi_i'((\partial D^k)\times D^{(n-1)-k}\times [0,\frac{1}{2}])\cap \partial (M\times [0,\frac{1}{2}]) \neq\emptyset$, then  $\phi_i'^{-1}(\partial (M\times [0,\frac{1}{2}]))\subseteq\partial D^k \times \partial D^{(n-1)-k} \times [0,\frac{1}{2}]$ and points
$\phi_i'^{-1}(\partial (M\times [0,\frac{1}{2}]))\subseteq\partial D^k \times \partial D^{(n-1)-k} \times [0,\frac{1}{2}]$ and points  $(p,t)\in \phi_i'(\partial D^k \times \partial D^{(n-1)-k} \times [0,\frac{1}{2}])=\phi_i(\partial D^k \times \partial D^{(n-1)-k})\times [0,\frac{1}{2}]$ get identified for all
$(p,t)\in \phi_i'(\partial D^k \times \partial D^{(n-1)-k} \times [0,\frac{1}{2}])=\phi_i(\partial D^k \times \partial D^{(n-1)-k})\times [0,\frac{1}{2}]$ get identified for all  $t\in [0,\frac{1}{2}]$. We can identify these points in the preimage already and thus identify
$t\in [0,\frac{1}{2}]$. We can identify these points in the preimage already and thus identify  $(x,y,t)\in \partial D^k \times \partial D^{(n-1)-k} \times [0,\frac{1}{2}]$ for all
$(x,y,t)\in \partial D^k \times \partial D^{(n-1)-k} \times [0,\frac{1}{2}]$ for all  $t\in [0,\frac{1}{2}]$ and abusively denote the quotient space by
$t\in [0,\frac{1}{2}]$ and abusively denote the quotient space by
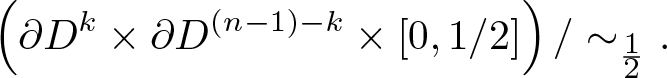 \begin{equation*}\left(\partial D^k \times \partial D^{(n-1)-k} \times [0,1/2]\right)/\sim_{\frac{1}{2}}.\end{equation*}
\begin{equation*}\left(\partial D^k \times \partial D^{(n-1)-k} \times [0,1/2]\right)/\sim_{\frac{1}{2}}.\end{equation*} Let ![]() $\phi_i^{\prime\prime}$ denote the map induced by
$\phi_i^{\prime\prime}$ denote the map induced by ![]() $\phi_i'$, then
$\phi_i'$, then
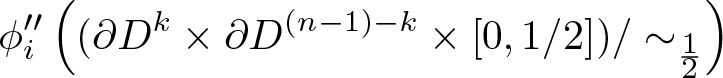 \begin{equation*}\phi_i^{\prime\prime}\left((\partial D^k \times \partial D^{(n-1)-k} \times [0,1/2])/\sim_{\frac{1}{2}}\right)\end{equation*}
\begin{equation*}\phi_i^{\prime\prime}\left((\partial D^k \times \partial D^{(n-1)-k} \times [0,1/2])/\sim_{\frac{1}{2}}\right)\end{equation*}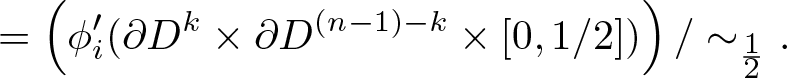 \begin{equation*}=\left(\phi_i'(\partial D^k \times \partial D^{(n-1)-k} \times [0,1/2])\right)/\sim_{\frac{1}{2}}.\end{equation*}
\begin{equation*}=\left(\phi_i'(\partial D^k \times \partial D^{(n-1)-k} \times [0,1/2])\right)/\sim_{\frac{1}{2}}.\end{equation*}This implies
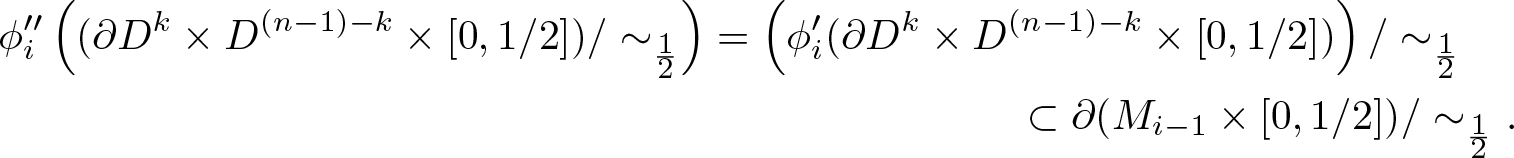 \begin{multline*} \phi_i^{\prime\prime}\left((\partial D^k \times D^{(n-1)-k}\times [0,1/2])/\sim_{\frac{1}{2}}\right)=\left(\phi_i'(\partial D^k \times D^{(n-1)-k}\times [0,1/2])\right)/\sim_{\frac{1}{2}}\\ \subset \partial(M_{i-1}\times[0,1/2])/\sim_{\frac{1}{2}}.
\end{multline*}
\begin{multline*} \phi_i^{\prime\prime}\left((\partial D^k \times D^{(n-1)-k}\times [0,1/2])/\sim_{\frac{1}{2}}\right)=\left(\phi_i'(\partial D^k \times D^{(n-1)-k}\times [0,1/2])\right)/\sim_{\frac{1}{2}}\\ \subset \partial(M_{i-1}\times[0,1/2])/\sim_{\frac{1}{2}}.
\end{multline*} To see that ![]() $\phi_i^{\prime\prime}$ is an n-dimensional k-handle in
$\phi_i^{\prime\prime}$ is an n-dimensional k-handle in  $(M\times[0,\frac{1}{2}])/\sim_{\frac{1}{2}}$, it remains to show that
$(M\times[0,\frac{1}{2}])/\sim_{\frac{1}{2}}$, it remains to show that  $\left(\partial D^k \times D^{(n-1)-k}\times [0,\frac{1}{2}]\right)/\sim_{\frac{1}{2}}$ is diffeomorphic to
$\left(\partial D^k \times D^{(n-1)-k}\times [0,\frac{1}{2}]\right)/\sim_{\frac{1}{2}}$ is diffeomorphic to ![]() $\partial D^k \times D^{n-k}$.
$\partial D^k \times D^{n-k}$.
It suffices to observe that  $\left(D^{(n-1)-k}\times [0,\frac{1}{2}]\right)/\sim_{\frac{1}{2}}$ is diffeomorphic to
$\left(D^{(n-1)-k}\times [0,\frac{1}{2}]\right)/\sim_{\frac{1}{2}}$ is diffeomorphic to ![]() $D^{n-k}$, where
$D^{n-k}$, where  $(y,t)\sim_{\frac{1}{2}}(y,t')$ for all
$(y,t)\sim_{\frac{1}{2}}(y,t')$ for all ![]() $y\in \partial D^{(n-1)-k}$, t,
$y\in \partial D^{(n-1)-k}$, t,  $t'\in [0,\frac{1}{2}]$. Map the equivalence class
$t'\in [0,\frac{1}{2}]$. Map the equivalence class ![]() $[D^{(n-1)-k}\times \{0\}]$ to the upper hemisphere of
$[D^{(n-1)-k}\times \{0\}]$ to the upper hemisphere of ![]() $D^{n-k}$, the equivalence class
$D^{n-k}$, the equivalence class  $[D^{(n-1)-k}\times \{\frac{1}{4}\}]$ to the disc bounded by the equator, the equivalence class
$[D^{(n-1)-k}\times \{\frac{1}{4}\}]$ to the disc bounded by the equator, the equivalence class  $[D^{(n-1)-k}\times \{\frac{1}{2}\}]$ to the lower hemisphere, and everything in between correspondingly.
$[D^{(n-1)-k}\times \{\frac{1}{2}\}]$ to the lower hemisphere, and everything in between correspondingly.
In Figure 4, we assume that the black and blue edges of the 1-handle ![]() $D^1\times D^1$ are in the boundary of M, so the rectangular faces spanned by them in the product
$D^1\times D^1$ are in the boundary of M, so the rectangular faces spanned by them in the product  $M\times [0,\frac{1}{2}]$ will each be collapsed to an edge in the half open book
$M\times [0,\frac{1}{2}]$ will each be collapsed to an edge in the half open book  $M\times [0,\frac{1}{2}]/\sim_{\frac{1}{2}}$.
$M\times [0,\frac{1}{2}]/\sim_{\frac{1}{2}}$.
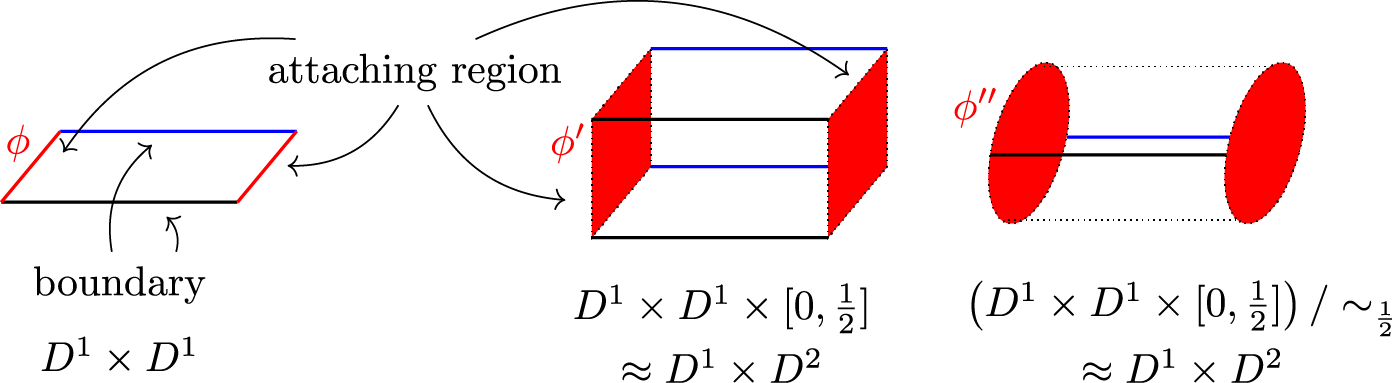
Figure 4. A 2-dimensional 1-handle inducing a 3-dimensional 1-handle.
From now on, let M be a compact 3-manifold with a non-empty boundary.
Algorithm 3.7.
Given a Heegaard diagram of M, one obtains a Kirby diagram of the half open book with page M by applying the following algorithm:
(1) Place the given Heegaard diagram in the yz-plane in
 $\mathbb{R}^3$, assuming the positive x-direction points out of the paper.
$\mathbb{R}^3$, assuming the positive x-direction points out of the paper.(2) Replace every 1-handle attaching region with a pair of D 3s as shown in Figure 5.

Figure 5. Replace every 1-handle attaching region in the given Heegaard diagram with a pair of D 3s.
(3) Add in the yz-plane a parallel knot to each 2-handle attaching sphere to indicate the blackboard framing.
Proof. By Proposition 3.6,  $M\times [0,\frac{1}{2}]$ and
$M\times [0,\frac{1}{2}]$ and  $M\times [0,\frac{1}{2}]/\sim_{\frac{1}{2}}$ admit equivalent handle decompositions and are diffeomorphic to each other, and thus
$M\times [0,\frac{1}{2}]/\sim_{\frac{1}{2}}$ admit equivalent handle decompositions and are diffeomorphic to each other, and thus  $M\times [0,\frac{1}{2}]$ and
$M\times [0,\frac{1}{2}]$ and  $M\times [0,\frac{1}{2}]/\sim_{\frac{1}{2}}$ share an equivalent Kirby diagram. Let us construct a Kirby diagram of the former one. A handle decomposition of M induces a handle decomposition of
$M\times [0,\frac{1}{2}]/\sim_{\frac{1}{2}}$ share an equivalent Kirby diagram. Let us construct a Kirby diagram of the former one. A handle decomposition of M induces a handle decomposition of  $M\times [0,\frac{1}{2}]$ in the following way:
$M\times [0,\frac{1}{2}]$ in the following way:
• A 3-dimensional 0-handle induces a 4-dimensional 0-handle. So we will now attach handles to
 $\partial D^4-\{$point
$\partial D^4-\{$point $\}\approx\mathbb{R}^3$ instead of to
$\}\approx\mathbb{R}^3$ instead of to  $\partial D^3-\{$point
$\partial D^3-\{$point $\}\approx\mathbb{R}^2$. Since Heegaard diagrams are defined in
$\}\approx\mathbb{R}^2$. Since Heegaard diagrams are defined in  $\mathbb{R}^2$, they can be embedded in the yz-plane in
$\mathbb{R}^2$, they can be embedded in the yz-plane in  $\mathbb{R}^3$.
$\mathbb{R}^3$.• A 3-dimensional 1-handle induces a 4-dimensional 1-handle. Thus, the attaching region of a 1-handle becomes a pair of D 3s.
• A 3-dimensional 2-handle induces a 4-dimensional 2-handle with framing given by the product structure of
 $M\times[0,\frac{1}{2}]$, which coincides with the blackboard framing.
$M\times[0,\frac{1}{2}]$, which coincides with the blackboard framing.
4. Kirby diagrams of 4-dimensional open books
By assumption, any 3-dimensional page and therefore any 4-dimensional half open book, with the induced handle decomposition (Proposition 3.6), have no 3-handles. Gluing a half open book with one 0-handle x 1-handles, and y 2-handles to a 4-manifold X along common boundary introduces y 2-handles, x 3-handles and one 4-handle, i.e. adds a y-component framed link to a Kirby diagram of X. Since an open book is obtained by gluing two half open books, we add a framed link to a Kirby diagram of the half open book to obtain a Kirby diagram of the open book.
4.1. Trivial monodromy
Let M be the page, a compact 3-manifold with non-empty boundary, as before. We denote the identity map on the page by ![]() $\operatorname{id}$.
$\operatorname{id}$.
Algorithm 4.1.
Given a Heegaard diagram of M, one obtains a Kirby diagram of the open book ![]() $\operatorname{Ob}(M,\operatorname{id})$ by applying the following algorithm:
$\operatorname{Ob}(M,\operatorname{id})$ by applying the following algorithm:
(1) Use Algorithm 3.7 to get a Kirby diagram of the half open book with page M.
(2) Add a 0-framed meridian to each blackboard-framed 2-handle attaching sphere in the Kirby diagram of the half open book.
Proof. By Proposition 3.4 and Remark 3.3, ![]() $\operatorname{Ob}(M,\varphi)$ is diffeomorphic to
$\operatorname{Ob}(M,\varphi)$ is diffeomorphic to  $D_{\varphi}(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})=D(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$ when the monodromy φ is (isotopic to) the identity map. For completeness, we summarize the proof given in [Reference Gompf and Stipsicz10] showing that adding a 0-framed meridian to each 2-handle attaching sphere in a Kirby diagram gives a Kirby diagram of the double.
$D_{\varphi}(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})=D(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$ when the monodromy φ is (isotopic to) the identity map. For completeness, we summarize the proof given in [Reference Gompf and Stipsicz10] showing that adding a 0-framed meridian to each 2-handle attaching sphere in a Kirby diagram gives a Kirby diagram of the double.
A handle decomposition on ![]() $DX=X\cup$handles is obtained by adding handles to X, where
$DX=X\cup$handles is obtained by adding handles to X, where  $X=M\times [0,\frac{1}{2}]/\sim_{\frac{1}{2}}$. It suffices to understand the induced 2-handles. A 2-handle h in X induces a 2-handle h ʹ in DX with the roles of core and cocore reversed. Since we are gluing using the identity map, the attaching map of an induced 2-handle
$X=M\times [0,\frac{1}{2}]/\sim_{\frac{1}{2}}$. It suffices to understand the induced 2-handles. A 2-handle h in X induces a 2-handle h ʹ in DX with the roles of core and cocore reversed. Since we are gluing using the identity map, the attaching map of an induced 2-handle ![]() $\varphi\colon \partial D^2\times D^2\rightarrow D^2\times \partial D^2\subset \partial X$ is given by interchanging the factors of
$\varphi\colon \partial D^2\times D^2\rightarrow D^2\times \partial D^2\subset \partial X$ is given by interchanging the factors of ![]() $\partial D^2\times D^2$. Thus, h ʹ is attached along the belt sphere of h, which is isotopic to a meridian of the attaching sphere of h. The framing of the induced 2-handle is given by the product framing coming from the product structure of the 2-handle
$\partial D^2\times D^2$. Thus, h ʹ is attached along the belt sphere of h, which is isotopic to a meridian of the attaching sphere of h. The framing of the induced 2-handle is given by the product framing coming from the product structure of the 2-handle ![]() $D^2\times D^2$, which coincides with the Seifert framing. Therefore, to get a Kirby diagram of the open book, add a 0-framed meridian to each 2-handle attaching sphere in a Kirby diagram of the half open book.
$D^2\times D^2$, which coincides with the Seifert framing. Therefore, to get a Kirby diagram of the open book, add a 0-framed meridian to each 2-handle attaching sphere in a Kirby diagram of the half open book.
Remark 4.2. The framings of a 4-dimensional 2-handle are classified by elements of ![]() $\pi_1(O(2))\approx \mathbb{Z}$. When the attaching sphere
$\pi_1(O(2))\approx \mathbb{Z}$. When the attaching sphere ![]() $\varphi(\partial D^2)$ bounds a Seifert surface, the attaching sphere can be pushed along it to give a parallel knot and hence a canonical choice of the 0-th framing.
$\varphi(\partial D^2)$ bounds a Seifert surface, the attaching sphere can be pushed along it to give a parallel knot and hence a canonical choice of the 0-th framing.
4.2. Non-trivial monodromy
Under the standard assumptions that handles are attached with non-decreasing indices to the boundary of handles of lower indices and that there are a unique 0-handle and no 3-handle, the cocore of a 2-handle in M is an arc in M with end-points in ![]() $\partial M$.
$\partial M$.
Proposition 4.3. The cocore of a 2-handle in the back cover of the half open book with page M corresponds to a half-meridian behind the yz-plane in a Kirby diagram of the half open book.
Proof. Recall that a Heegaard diagram of M records where 1- and 2-handles are attached to the boundary of the 0-handle. Situate a Heegaard diagram in the yz-plane of ![]() $\mathbb{R}^3$, and view the region in front of the yz-plane as the interior of the 0-handle and the yz-plane as the boundary of the 0-handle (with a point removed). A 2-handle of M is being attached to
$\mathbb{R}^3$, and view the region in front of the yz-plane as the interior of the 0-handle and the yz-plane as the boundary of the 0-handle (with a point removed). A 2-handle of M is being attached to ![]() $\partial D^3$ from behind the yz-plane in this perspective.
$\partial D^3$ from behind the yz-plane in this perspective.
Now, we recall the construction of a Kirby diagram of a half open book. We place a Heegaard diagram of the page in the yz-plane in ![]() $\mathbb{R}^3$, replace each D 2 with a D 3 and add blackboard framing to each 2-handle attaching sphere. The blank space in
$\mathbb{R}^3$, replace each D 2 with a D 3 and add blackboard framing to each 2-handle attaching sphere. The blank space in ![]() $\mathbb{R}^3$ is the boundary of the half open book, which consists of two copies of M, namely, the front and back covers. Without loss of generality, we may identify the region behind the yz-plane with the back cover and the region in front of the yz-plane with the front cover. Thus, the cocore of a 2-handle in the back cover corresponds to a half-meridian, with end-points on the yz-plane, of the 2-handle attaching sphere as shown in Figure 6. Similarly, a half-meridian in front of the yz-plane corresponds to the cocore of a 2-handle in the front cover.
$\mathbb{R}^3$ is the boundary of the half open book, which consists of two copies of M, namely, the front and back covers. Without loss of generality, we may identify the region behind the yz-plane with the back cover and the region in front of the yz-plane with the front cover. Thus, the cocore of a 2-handle in the back cover corresponds to a half-meridian, with end-points on the yz-plane, of the 2-handle attaching sphere as shown in Figure 6. Similarly, a half-meridian in front of the yz-plane corresponds to the cocore of a 2-handle in the front cover.
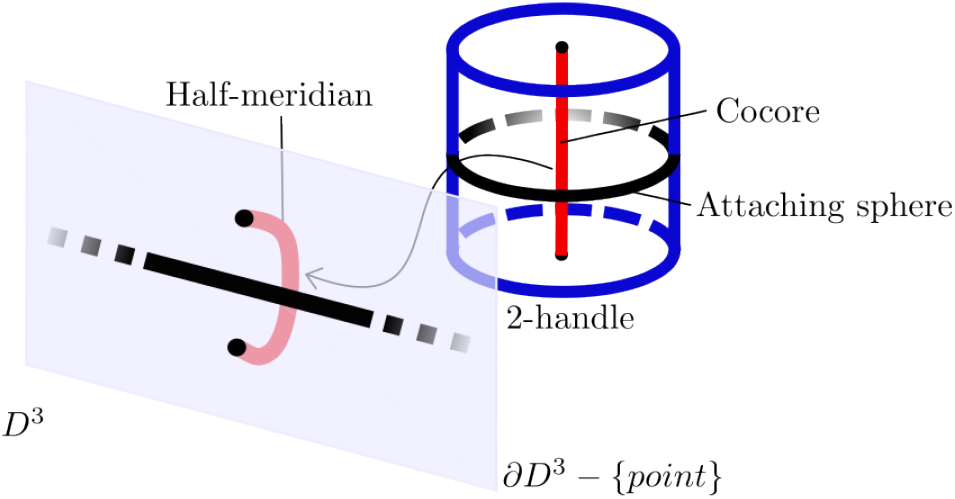
Figure 6. Attaching a 2-handle along ![]() $\partial D^3$.
$\partial D^3$.
Algorithm 4.4.
Given a Heegaard diagram of M and the image under the monodromy φ of each 2-handle in M, one obtains a Kirby diagram of the open book ![]() $\operatorname{Ob}(M,\varphi)$ by applying the following algorithm:
$\operatorname{Ob}(M,\varphi)$ by applying the following algorithm:
(1) Use Algorithm 3.7 to get a Kirby diagram of the half open book with page M.
(2) Add behind the yz-plane a half-meridian with blackboard framing to each 2-handle attaching sphere in the Kirby diagram of the half open book as in Figure 7.

Figure 7. Step 2 of Algorithm 4.4.
(3) Add in front of the yz-plane a half-meridian with blackboard framing to each 2-handle attaching sphere in the Kirby diagram of the half open book and then replace them with their images under φ.
Proof. By Proposition 3.4, ![]() $\operatorname{Ob}(M,\varphi)$ is diffeomorphic to
$\operatorname{Ob}(M,\varphi)$ is diffeomorphic to  $D_{\varphi}(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$, and the goal is to construct a Kirby diagram of
$D_{\varphi}(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$, and the goal is to construct a Kirby diagram of  $D_{\varphi}(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$. Recall that the boundary of the half open book
$D_{\varphi}(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$. Recall that the boundary of the half open book  $M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$ consists of front and back covers, which are diffeomorphic to the page M.
$M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$ consists of front and back covers, which are diffeomorphic to the page M.
Let us focus on the Kirby diagram of the half open book lying in the yz-plane in ![]() $\mathbb{R}^3$ provided by Algorithm 3.7. Figures 8 and 9 provide a running example. The blank space in a Kirby diagram of a manifold without 3- and 4-handles represents a subset of the boundary. We identify the region in front of and behind the yz-plane with the front and back cover of the half open book, respectively, as described in the proof of Proposition 4.3. The yz-plane itself, where the front and back covers meet, corresponds to the binding
$\mathbb{R}^3$ provided by Algorithm 3.7. Figures 8 and 9 provide a running example. The blank space in a Kirby diagram of a manifold without 3- and 4-handles represents a subset of the boundary. We identify the region in front of and behind the yz-plane with the front and back cover of the half open book, respectively, as described in the proof of Proposition 4.3. The yz-plane itself, where the front and back covers meet, corresponds to the binding  $\partial M\subset M\times [0,\frac{1}{2}]/\sim_{\frac{1}{2}}$.
$\partial M\subset M\times [0,\frac{1}{2}]/\sim_{\frac{1}{2}}$.
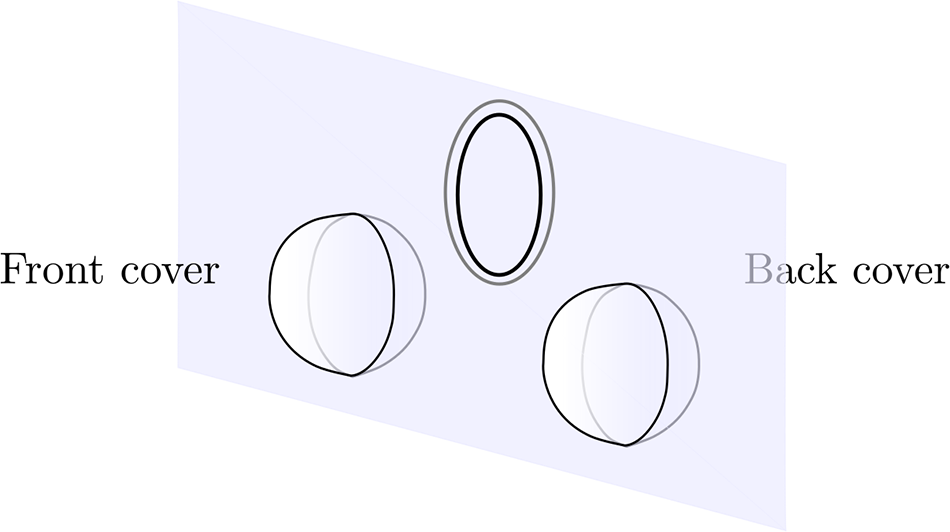
Figure 8. Kirby diagram of half open book (with page punctured solid torus).
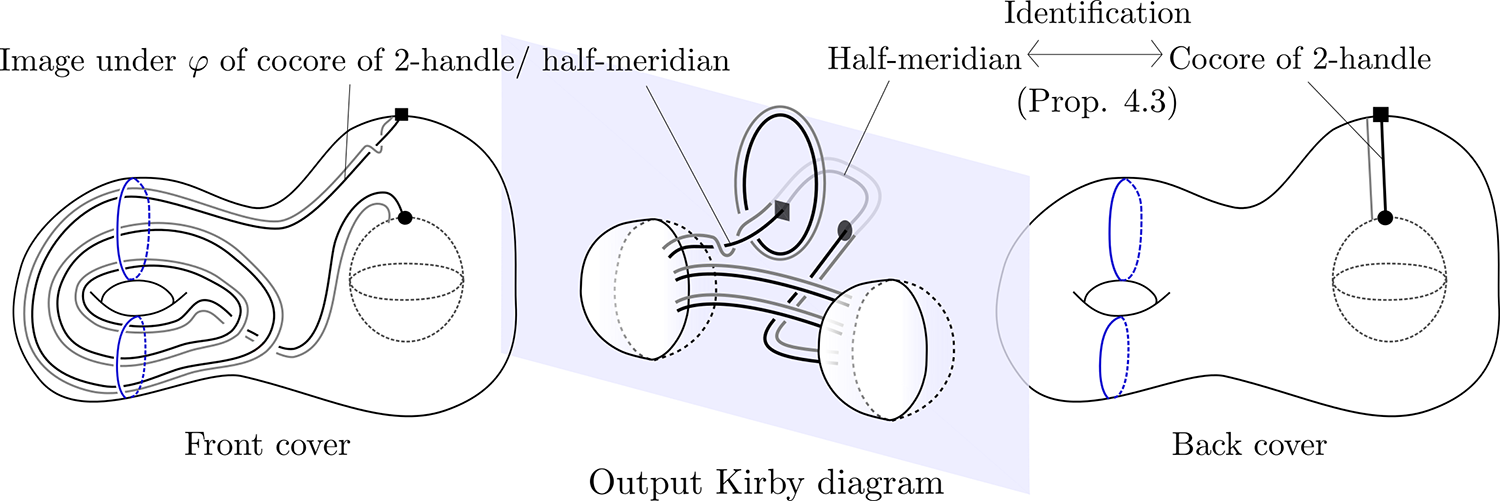
Figure 9. Kirby diagram of open book with page punctured solid torus and monodromy with the composition of 3 torus twists (Defintion 6.2).
Also recall that Definition 3.2,  $D_{\varphi}(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$ is obtained by gluing two copies of
$D_{\varphi}(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$ is obtained by gluing two copies of  $M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$ along the boundary. Namely,
$M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$ along the boundary. Namely,
• glue the front cover of the second copy to the back cover of the first copy with the identity map and
• glue the back cover of the second to the front cover of the first with the given monodromy φ.
A handle decomposition on  $D_{\varphi}(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$ is obtained by adding handles to the half open book
$D_{\varphi}(M\times [0,\frac{1}{2}]/\sim_\frac{1}{2})$ is obtained by adding handles to the half open book  $M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$. It suffices to understand the induced 2-handles. The attaching sphere of an induced 2-handle is the union of ‘two attaching arcs’, one in the front and one in the back cover. In the back cover, where the gluing map is the identity map, the attaching arc is given by a half-meridian of the 2-handle attaching sphere as in the proof of Algorithm 4.1. In the front cover, the gluing map is given by the monodromy φ and not the identity map. Hence, instead of a half-meridian, the attaching arc is given by the image under φ of the half-meridian. Using the identification of a half-meridian with the cocore of a 2-handle (Proposition 4.3), we conclude that in the front cover, the attaching arc is given by the image of the cocore of the 2-handle. Similarly, a framing indicating parallel knot consists of two arcs: a parallel arc of the half-meridian behind the yz-plane and the image under φ of a parallel arc of the half-meridian (or cocore of 2-handle) in the other half-space.
$M\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$. It suffices to understand the induced 2-handles. The attaching sphere of an induced 2-handle is the union of ‘two attaching arcs’, one in the front and one in the back cover. In the back cover, where the gluing map is the identity map, the attaching arc is given by a half-meridian of the 2-handle attaching sphere as in the proof of Algorithm 4.1. In the front cover, the gluing map is given by the monodromy φ and not the identity map. Hence, instead of a half-meridian, the attaching arc is given by the image under φ of the half-meridian. Using the identification of a half-meridian with the cocore of a 2-handle (Proposition 4.3), we conclude that in the front cover, the attaching arc is given by the image of the cocore of the 2-handle. Similarly, a framing indicating parallel knot consists of two arcs: a parallel arc of the half-meridian behind the yz-plane and the image under φ of a parallel arc of the half-meridian (or cocore of 2-handle) in the other half-space.
5. Examples
Given ![]() $g,n\geq0$, let
$g,n\geq0$, let ![]() $H_{g,n}$ denote the punctured handlebody obtained from a 0-handle D 3 by attaching g 1-handles and n 2-handles to
$H_{g,n}$ denote the punctured handlebody obtained from a 0-handle D 3 by attaching g 1-handles and n 2-handles to ![]() $\partial D^3$. For example,
$\partial D^3$. For example, ![]() $H_{1,0}$ is a solid torus and
$H_{1,0}$ is a solid torus and ![]() $H_{0,1}$ is a punctured ball. When
$H_{0,1}$ is a punctured ball. When ![]() $g=n=1$, the punctured handlebody is also referred to as a punctured solid torus (Figure 2). A punctured handlebody has a canonical handle decomposition and hence a canonical Heegaard diagram as shown in Figure 10.
$g=n=1$, the punctured handlebody is also referred to as a punctured solid torus (Figure 2). A punctured handlebody has a canonical handle decomposition and hence a canonical Heegaard diagram as shown in Figure 10.
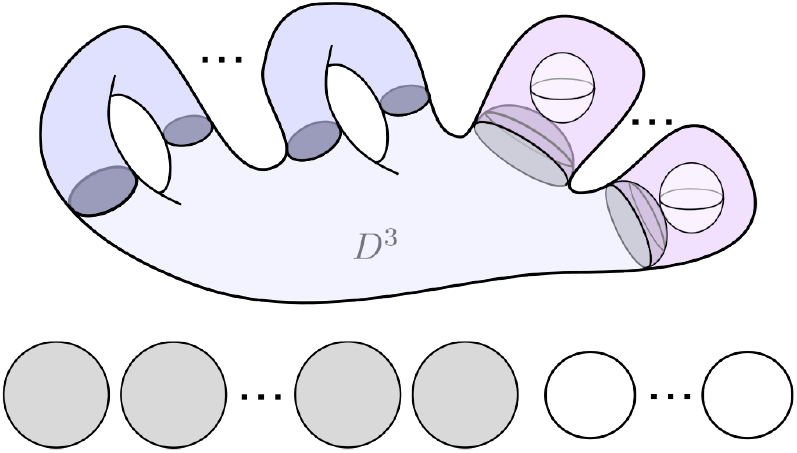
Figure 10. A punctured handlebody and its Heegaard diagram.
5.1. Constructing Heegaard diagrams of 3-dimensional open books
The construction of a Heegaard diagram of a 3-dimensional open book using half open books is more straightforward, and thus it is a good idea to see an example in dimension 3 before returning to dimension 4. We carefully go through the construction of a Heegaard diagram of the 3-dimensional open book ![]() $\operatorname{Ob}(D^2\cup h^1,\psi)$ with page annulus. The method essentially follows [Reference Honda, Kazez and Matić13].
$\operatorname{Ob}(D^2\cup h^1,\psi)$ with page annulus. The method essentially follows [Reference Honda, Kazez and Matić13].
The half open book  $(D^2\cup h^1)\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$ is a solid torus
$(D^2\cup h^1)\times [0,\frac{1}{2}]/\sim_\frac{1}{2}$ is a solid torus ![]() $H_{1,0}$ as visualized in Figure 11, whose canonical Heegaard diagram consists of a pair of D 2s. Let L be a line in
$H_{1,0}$ as visualized in Figure 11, whose canonical Heegaard diagram consists of a pair of D 2s. Let L be a line in ![]() $\mathbb{R}^2$ going through the centres of the pair of D 2s, then the two regions separated by L correspond to the front and back covers of the half open book. We only need to take care of the attaching sphere of the 2-handle induced by the 1-handle of
$\mathbb{R}^2$ going through the centres of the pair of D 2s, then the two regions separated by L correspond to the front and back covers of the half open book. We only need to take care of the attaching sphere of the 2-handle induced by the 1-handle of ![]() $D^2\cup h^1$.
$D^2\cup h^1$.

Figure 11. Left to right: ![]() $D^2\cup h^1$,
$D^2\cup h^1$,  $(D^2\cup h^1)\times [0,\frac{1}{2}]$,
$(D^2\cup h^1)\times [0,\frac{1}{2}]$,  $(D^2\cup h^1)\times [0,\frac{1}{2}]/\sim_{\frac{1}{2}}$.
$(D^2\cup h^1)\times [0,\frac{1}{2}]/\sim_{\frac{1}{2}}$.
When the monodromy ![]() $\psi=\operatorname{id}$ is trivial, add a meridian around D 2, because the attaching sphere coincides with the belt sphere of the 1-handle. We obtain a Heegaard diagram of
$\psi=\operatorname{id}$ is trivial, add a meridian around D 2, because the attaching sphere coincides with the belt sphere of the 1-handle. We obtain a Heegaard diagram of ![]() $S^1\times S^2$ as illustrated in Figure 12. This is expected since
$S^1\times S^2$ as illustrated in Figure 12. This is expected since ![]() $\operatorname{Ob}(D^2\cup h^1,\operatorname{id})$ is diffeomorphic to
$\operatorname{Ob}(D^2\cup h^1,\operatorname{id})$ is diffeomorphic to ![]() $DH_{1,0}$, and the double of a solid torus is diffeomorphic to
$DH_{1,0}$, and the double of a solid torus is diffeomorphic to ![]() $S^1\times S^2$.
$S^1\times S^2$.
Figure 12. ![]() $\operatorname{Ob}(D^2\cup h^1,\operatorname{id})$ is diffeomorphic to
$\operatorname{Ob}(D^2\cup h^1,\operatorname{id})$ is diffeomorphic to ![]() $S^1\times S^2$.
$S^1\times S^2$.
Now, we consider the monodromy ψ given by the composition of three Dehn twists along the core of the annulus. The Heegaard diagrams of ![]() $\operatorname{Ob}(D^2\cup h^1,\psi)$ and
$\operatorname{Ob}(D^2\cup h^1,\psi)$ and ![]() $\operatorname{Ob}(D^2\cup h^1,\operatorname{id})$ should look the same on one side of L since we always glue using the identity map on the back cover. Without loss of generality, add a half meridian to a D 2 below L. The non-trivial monodromy only plays a role above L in the front cover of the half open book. Since the image of the cocore of the 1-handle is an arc in
$\operatorname{Ob}(D^2\cup h^1,\operatorname{id})$ should look the same on one side of L since we always glue using the identity map on the back cover. Without loss of generality, add a half meridian to a D 2 below L. The non-trivial monodromy only plays a role above L in the front cover of the half open book. Since the image of the cocore of the 1-handle is an arc in ![]() $D^2\cup h^1$ running thrice through the 1-handle, we add an arc above L that intersects the D 2 thrice before joining with the half meridian as reflected in Figure 13. We obtain a Heegaard diagram of the lens space
$D^2\cup h^1$ running thrice through the 1-handle, we add an arc above L that intersects the D 2 thrice before joining with the half meridian as reflected in Figure 13. We obtain a Heegaard diagram of the lens space ![]() $\operatorname{L}(3,1)$, which will be defined in Section 5.3.
$\operatorname{L}(3,1)$, which will be defined in Section 5.3.
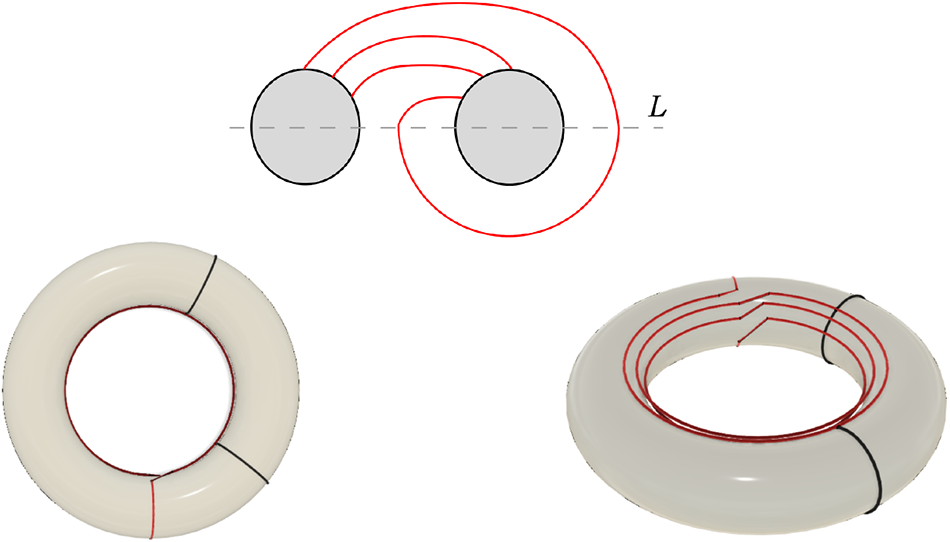
Figure 13. The attaching sphere (red) of the induced 2-handle is marked on the Heegaard diagram (top), on the back cover (left) and on the front cover (right) of the half open book ![]() $H_{1,0}$.
$H_{1,0}$.
5.2. 2-sphere bundles over 2-sphere
Now, we construct a Kirby diagram of the open book with page punctured ball ![]() $H_{0,1}$ and trivial monodromy. The punctured ball is obtained by removing an open ball from D 3, or it can also be obtained by attaching a single 2-handle to D 3. This handle decomposition gives rise to a Heegaard diagram consisting of a single unknot. Using Algorithm 3.7, we obtain a Kirby diagram of the half open book consisting of an unknot with blackboard framing, which is a Kirby diagram of
$H_{0,1}$ and trivial monodromy. The punctured ball is obtained by removing an open ball from D 3, or it can also be obtained by attaching a single 2-handle to D 3. This handle decomposition gives rise to a Heegaard diagram consisting of a single unknot. Using Algorithm 3.7, we obtain a Kirby diagram of the half open book consisting of an unknot with blackboard framing, which is a Kirby diagram of ![]() $D^2\times S^2$ [Reference Gompf and Stipsicz10, p. 120]. Finally, apply Step 2 of Algorithm 4.1 to get a Hopf link with each component labeled 0 as in Figure 14(c). It is well known that the output is a Kirby diagram of the trivial S 2-bundle over S 2 [Reference Gompf and Stipsicz10, p. 127], and thus
$D^2\times S^2$ [Reference Gompf and Stipsicz10, p. 120]. Finally, apply Step 2 of Algorithm 4.1 to get a Hopf link with each component labeled 0 as in Figure 14(c). It is well known that the output is a Kirby diagram of the trivial S 2-bundle over S 2 [Reference Gompf and Stipsicz10, p. 127], and thus ![]() $\operatorname{Ob}(H_{0,1},\operatorname{id})$ is diffeomorphic to
$\operatorname{Ob}(H_{0,1},\operatorname{id})$ is diffeomorphic to ![]() $S^2\times S^2$.
$S^2\times S^2$.
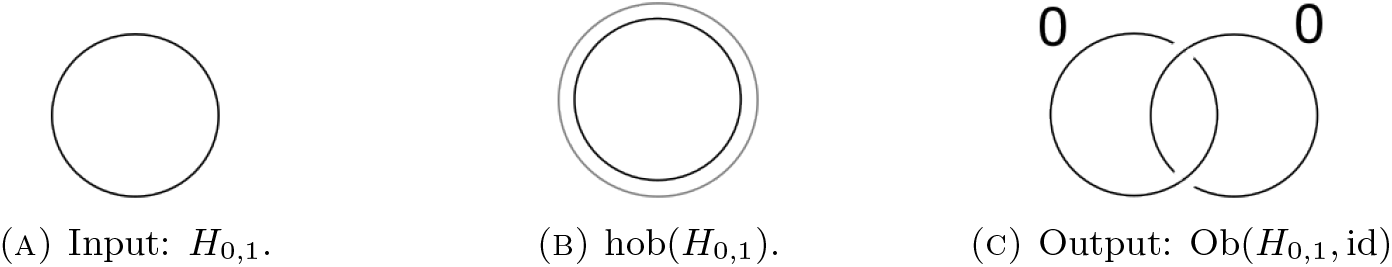
Figure 14. Applying Algorithm 4.1.
The mapping class group of the punctured ball ![]() $H_{0,1}$, denoted by
$H_{0,1}$, denoted by
is the group of isotopy classes of orientation-preserving diffeomorphisms of the punctured ball that fix the boundary pointwise. Elements in ![]() $\operatorname{MCG}(H_{0,1},\partial H_{0,1})$ are equivalent to the isotopy classes of loops in the space Ω of all orientation-preserving diffeomorphisms of S 2. Ω deformation retracts to the rotation group
$\operatorname{MCG}(H_{0,1},\partial H_{0,1})$ are equivalent to the isotopy classes of loops in the space Ω of all orientation-preserving diffeomorphisms of S 2. Ω deformation retracts to the rotation group ![]() $\operatorname{SO}(3)$ [Reference Smale27], and thus
$\operatorname{SO}(3)$ [Reference Smale27], and thus
Consequently, there can be at most two non-diffeomorphic open books with the punctured ball as page. The generator of ![]() $\operatorname{MCG}(H_{0,1},\partial H_{0,1})$ is given by a boundary parallel sphere twist σ (Defintion 6.1) as discussed in [Reference Brendle, Broaddus and Putman3, Lemma 2.5]. Construction of a Kirby diagram of
$\operatorname{MCG}(H_{0,1},\partial H_{0,1})$ is given by a boundary parallel sphere twist σ (Defintion 6.1) as discussed in [Reference Brendle, Broaddus and Putman3, Lemma 2.5]. Construction of a Kirby diagram of ![]() $\operatorname{Ob}(H_{0,1},\sigma)$ using Algorithm 4.4 is demonstrated in Figure 15.
$\operatorname{Ob}(H_{0,1},\sigma)$ using Algorithm 4.4 is demonstrated in Figure 15.
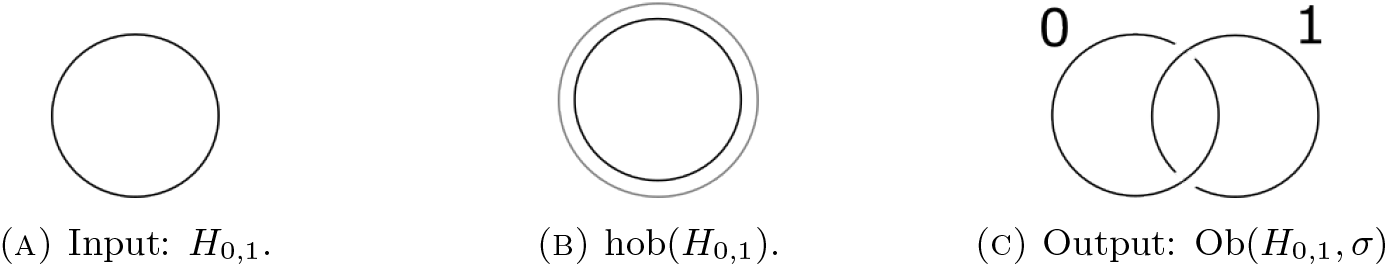
Figure 15. Using Algorithm 4.4, we observe that ![]() $\operatorname{Ob}(H_{0,1},\sigma)$ is diffeomorphic to
$\operatorname{Ob}(H_{0,1},\sigma)$ is diffeomorphic to ![]() $S^2 \tilde{\times} S^2$, the twisted S 2-bundle over S 2.
$S^2 \tilde{\times} S^2$, the twisted S 2-bundle over S 2.
Let ![]() $(\sigma)^n=\sigma\circ\dots\circ\sigma$ denote the composition of n sphere twists, which changes the framing of the cocore by n.
$(\sigma)^n=\sigma\circ\dots\circ\sigma$ denote the composition of n sphere twists, which changes the framing of the cocore by n. ![]() $(\sigma)^n$ is isotopic to the identity map when n is even and isotopic to a single sphere twist when n is odd because a sphere twist generates
$(\sigma)^n$ is isotopic to the identity map when n is even and isotopic to a single sphere twist when n is odd because a sphere twist generates ![]() $\operatorname{MCG}(H_{0,1},\partial H_{0,1})\approx\mathbb{Z}/2\mathbb{Z}$. According to Algorithm 4.4,
$\operatorname{MCG}(H_{0,1},\partial H_{0,1})\approx\mathbb{Z}/2\mathbb{Z}$. According to Algorithm 4.4, ![]() $\operatorname{Ob}(H_{0,1},(\sigma)^n)$ has a Kirby diagram consisting of a Hopf link labeled 0 and n. This shows that the diffeomorphism type of the 4-manifold represented by the Hopf link labeled 0 and n only depends on the parity of n [Reference Gompf and Stipsicz10, 130], as summarized in Figure 16.
$\operatorname{Ob}(H_{0,1},(\sigma)^n)$ has a Kirby diagram consisting of a Hopf link labeled 0 and n. This shows that the diffeomorphism type of the 4-manifold represented by the Hopf link labeled 0 and n only depends on the parity of n [Reference Gompf and Stipsicz10, 130], as summarized in Figure 16.
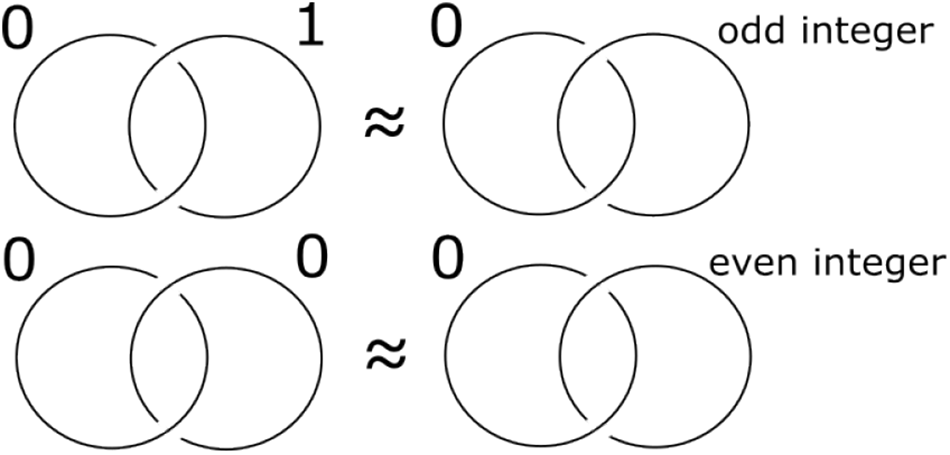
Figure 16. ![]() $S^2\tilde{\times} S^2$ (top) and
$S^2\tilde{\times} S^2$ (top) and ![]() $S^2\times S^2$ (bottom): the only two open books with the punctured ball as page.
$S^2\times S^2$ (bottom): the only two open books with the punctured ball as page.
5.3. Spun and twist spun lens spaces
Let ![]() $p,q$ be relatively prime, non-negative integers. The lens space
$p,q$ be relatively prime, non-negative integers. The lens space
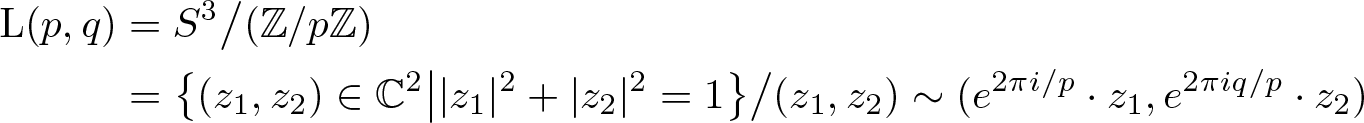 \begin{align*} \operatorname{L}(p,q)&=S^3\big/(\mathbb{Z}/p\mathbb{Z})\\ &=\big\{(z_1,z_2)\in\mathbb{C}^2\big| |z_1|^2+|z_2|^2=1\big\}\big/(z_1,z_2)\sim(e^{2\pi i/p}\cdot z_1,e^{2\pi iq/p}\cdot z_2) \end{align*}
\begin{align*} \operatorname{L}(p,q)&=S^3\big/(\mathbb{Z}/p\mathbb{Z})\\ &=\big\{(z_1,z_2)\in\mathbb{C}^2\big| |z_1|^2+|z_2|^2=1\big\}\big/(z_1,z_2)\sim(e^{2\pi i/p}\cdot z_1,e^{2\pi iq/p}\cdot z_2) \end{align*} is a closed 3-manifold, which can also be obtained by gluing together two solid tori with a diffeomorphism on the boundary that takes a meridian of one torus to a curve ![]() $-p\lambda+q\mu$ on the other torus, where λ and µ denote the longitude and meridian, respectively. The solid torus can be decomposed into a 0-handle and a 1-handle. Therefore, a lens space can be decomposed into a 0-handle, a 1-handle, a 2-handle and a 3-handle. (The 2- and 3-handles are induced by the 0- and 1-handles.) To get a handle decomposition of the punctured lens space
$-p\lambda+q\mu$ on the other torus, where λ and µ denote the longitude and meridian, respectively. The solid torus can be decomposed into a 0-handle and a 1-handle. Therefore, a lens space can be decomposed into a 0-handle, a 1-handle, a 2-handle and a 3-handle. (The 2- and 3-handles are induced by the 0- and 1-handles.) To get a handle decomposition of the punctured lens space ![]() $\operatorname{L}(p,q)-D^3$, simply remove the 3-handle. This handle decomposition leads to a Heegaard diagram of
$\operatorname{L}(p,q)-D^3$, simply remove the 3-handle. This handle decomposition leads to a Heegaard diagram of ![]() $\operatorname{L}(p,q)-D^3$ as depicted in Figure 17(a).
$\operatorname{L}(p,q)-D^3$ as depicted in Figure 17(a).
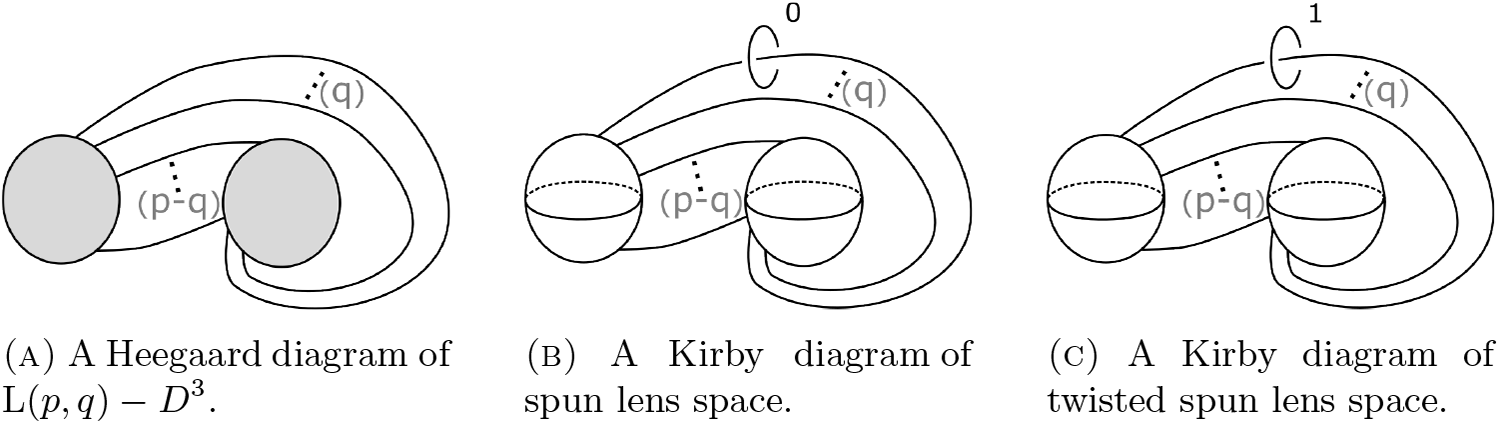
Figure 17. For clarity, blackboard framing is omitted here.
Figure 18 demonstrates the construction of a Kirby diagram of the open book ![]() $\operatorname{Ob}(\operatorname{L}(3,1)-D^3,\operatorname{id})$ using Algorithm 4.1.
$\operatorname{Ob}(\operatorname{L}(3,1)-D^3,\operatorname{id})$ using Algorithm 4.1.
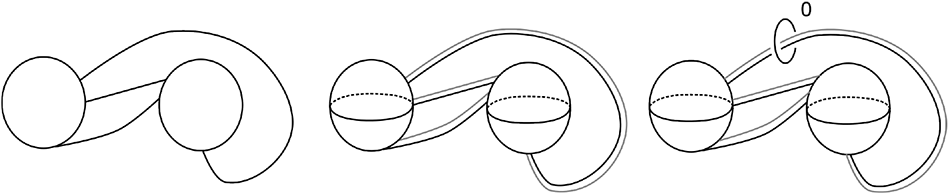
Figure 18. Left to right: input Heegaard diagram of ![]() $\operatorname{L}(3,1)-D^3$, a Kirby diagram of half open book with page
$\operatorname{L}(3,1)-D^3$, a Kirby diagram of half open book with page ![]() $\operatorname{L}(3,1)-D^3$ and output Kirby diagram of the open book
$\operatorname{L}(3,1)-D^3$ and output Kirby diagram of the open book ![]() $\operatorname{Ob}(\operatorname{L}(3,1)-D^3,\operatorname{id})$.
$\operatorname{Ob}(\operatorname{L}(3,1)-D^3,\operatorname{id})$.
Given a closed 3-manifold M, let ![]() $\mathring{M}$ denote M with an open 3-ball removed. Gordon [Reference Gordon11] defines the spin of M to be obtained in gluing
$\mathring{M}$ denote M with an open 3-ball removed. Gordon [Reference Gordon11] defines the spin of M to be obtained in gluing ![]() $\mathring{M}\times S^1$ to
$\mathring{M}\times S^1$ to ![]() $S^2\times D^2$ using the identity map on the boundary
$S^2\times D^2$ using the identity map on the boundary ![]() $\operatorname{id}_{S^2\times S^1}$. Observe that the open book
$\operatorname{id}_{S^2\times S^1}$. Observe that the open book ![]() $\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\operatorname{id})$ is the spin of a lens space, also known as a spun lens space. One obtains a Kirby diagram of a spun lens space as illustrated by Figure 17.
$\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\operatorname{id})$ is the spin of a lens space, also known as a spun lens space. One obtains a Kirby diagram of a spun lens space as illustrated by Figure 17.
The twisted spin of M is obtained by gluing ![]() $\mathring{M}\times S^1$ to
$\mathring{M}\times S^1$ to ![]() $S^2\times D^2$ by the unique self-diffeomorphism of
$S^2\times D^2$ by the unique self-diffeomorphism of ![]() $S^2 \times S^1$ not extending over
$S^2 \times S^1$ not extending over ![]() $S^2 \times D^2$ [Reference Gluck9]. Since twisted spin of the lens space
$S^2 \times D^2$ [Reference Gluck9]. Since twisted spin of the lens space ![]() $\operatorname{L}(p,q)$ is diffeomorphic to
$\operatorname{L}(p,q)$ is diffeomorphic to ![]() $\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\sigma)$, where σ is a boundary parallel sphere twist (Defintion 6.1), we can apply Algorithm 4.4.
$\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\sigma)$, where σ is a boundary parallel sphere twist (Defintion 6.1), we can apply Algorithm 4.4.
5.4. Open books with page handlebody
Let us look at Kirby diagrams of the family of open books with page handlebody ![]() $H_{g,0}$,
$H_{g,0}$, ![]() $g\geq0$. Starting with the most basic case g = 0 and trivial monodromy, we would like to construct a Kirby diagram of
$g\geq0$. Starting with the most basic case g = 0 and trivial monodromy, we would like to construct a Kirby diagram of ![]() $\operatorname{Ob}(D^3,\operatorname{id})$ using two different input Heegaard diagrams of D 3. Firstly, the empty diagram is by definition the result of attaching nothing to D 3 and thus is a Heegaard diagram of D 3. The empty diagram remains empty after applying each step in Algorithm 4.1, and thus we obtain a Kirby diagram of S 4. Secondly, by handle cancellation [Reference Gompf and Stipsicz10, Proposition 4.2.9], the ‘dumbbell’ as illustrated in Figure 19 is another Heegaard diagram of D 3. By handle cancellation, the output of Algorithm 4.1 is again a Kirby diagram of S 4. Therefore, independent of the choice of input, we conclude that
$\operatorname{Ob}(D^3,\operatorname{id})$ using two different input Heegaard diagrams of D 3. Firstly, the empty diagram is by definition the result of attaching nothing to D 3 and thus is a Heegaard diagram of D 3. The empty diagram remains empty after applying each step in Algorithm 4.1, and thus we obtain a Kirby diagram of S 4. Secondly, by handle cancellation [Reference Gompf and Stipsicz10, Proposition 4.2.9], the ‘dumbbell’ as illustrated in Figure 19 is another Heegaard diagram of D 3. By handle cancellation, the output of Algorithm 4.1 is again a Kirby diagram of S 4. Therefore, independent of the choice of input, we conclude that ![]() $\operatorname{Ob}(D^3,\operatorname{id})$ is diffeomorphic to S 4.
$\operatorname{Ob}(D^3,\operatorname{id})$ is diffeomorphic to S 4.

Figure 19. Left to right: a Heegaard diagram of D 3 and a Kirby diagram of half open book with page D 3, a Kirby diagram of S 4.
Given g > 0, each one of the g 1-handles of the page ![]() $H_{g,0}$ induces a 1-handle of
$H_{g,0}$ induces a 1-handle of ![]() $\operatorname{hob}(H_{g,0})$. Thus,
$\operatorname{hob}(H_{g,0})$. Thus, ![]() $\operatorname{hob}(H_{g,0})$ is diffeomorphic to the result
$\operatorname{hob}(H_{g,0})$ is diffeomorphic to the result ![]() $\#_g S^1\times D^3$ of attaching g 1-handles to D 4. A Kirby diagram of this manifold with a non-empty boundary, as given by Algorithm 3.7, consists of g pairs of D 3s. Since an open book with trivial monodromy is obtained by taking the double of the half open book,
$\#_g S^1\times D^3$ of attaching g 1-handles to D 4. A Kirby diagram of this manifold with a non-empty boundary, as given by Algorithm 3.7, consists of g pairs of D 3s. Since an open book with trivial monodromy is obtained by taking the double of the half open book, ![]() $\operatorname{Ob}(H_{g,0},\operatorname{id})$ is diffeomorphic
$\operatorname{Ob}(H_{g,0},\operatorname{id})$ is diffeomorphic ![]() $\#_g S^1\times S^3$. The output Kirby diagram of Algorithm 4.1,also consisting of g pairs of D 3s, should be interpreted as the closed manifold
$\#_g S^1\times S^3$. The output Kirby diagram of Algorithm 4.1,also consisting of g pairs of D 3s, should be interpreted as the closed manifold ![]() $\#_g S^1\times S^3$.
$\#_g S^1\times S^3$.
Algorithms 4.1 and 4.4 are done after the first step in the absence of 2-handles. Consequently, the output Kirby diagram of ![]() $\operatorname{Ob}(H_{g,0},\operatorname{id})$ coincides with the output Kirby diagram of
$\operatorname{Ob}(H_{g,0},\operatorname{id})$ coincides with the output Kirby diagram of ![]() $\operatorname{Ob}(H_{g,0},\varphi)$ for any monodromy
$\operatorname{Ob}(H_{g,0},\varphi)$ for any monodromy ![]() $\varphi\colon H_{g,0}\rightarrow H_{g,0}$. This reflects the triviality of the mapping class group
$\varphi\colon H_{g,0}\rightarrow H_{g,0}$. This reflects the triviality of the mapping class group ![]() $\operatorname{MCG}(H_{g,0},\partial H_{g,0})$— two diffeomorphisms
$\operatorname{MCG}(H_{g,0},\partial H_{g,0})$— two diffeomorphisms ![]() $F, F'$ on
$F, F'$ on ![]() $H_{g,0}$ are isotopic if and only if their restrictions
$H_{g,0}$ are isotopic if and only if their restrictions ![]() $\partial F, \partial F'$ to the boundary are isotopic [Reference Hensel12].
$\partial F, \partial F'$ to the boundary are isotopic [Reference Hensel12].
6. Open books with page punctured solid torus
The goal of this section is to introduce notions and techniques in preparation for Section 7. Firstly, we define so-called torus twist and sphere twist monodromies on a punctured handlebody. Then, we construct a Kirby diagram of an open book with page punctured solid torus and monodromy a composition of torus and sphere twists. It turns out that such twists provide us with sufficiently many monodromies needed in the proof of Theorem 7.2. Finally, we show how to obtain an entire family of Kirby diagrams of an open book with page punctured solid torus and monodromy with a composition of torus and sphere twists.
6.1. Twists along sphere and torus
Let S be an embedded surface with trivial normal bundle in a 3-manifold M. Identifying a regular neighbourhood of S in M with ![]() $S \times [0,1]$ and choosing a representation ft of a generator of
$S \times [0,1]$ and choosing a representation ft of a generator of ![]() $\pi_1(\operatorname{Diff}(S),\operatorname{id})$ give rise to a monodromy on M called twist along S given by
$\pi_1(\operatorname{Diff}(S),\operatorname{id})$ give rise to a monodromy on M called twist along S given by
 \begin{equation*}
\begin{cases}
f_t\times \operatorname{id_{[0,1]}} & \text{on } S\times [0,1], \\
\operatorname{id} & \text{elsewhere.}
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
f_t\times \operatorname{id_{[0,1]}} & \text{on } S\times [0,1], \\
\operatorname{id} & \text{elsewhere.}
\end{cases}
\end{equation*} Note that properly embedded spheres and tori are the only closed, orientable surfaces for which the group ![]() $\pi_1(\operatorname{Diff}(S),\operatorname{id})$ is non-trivial [Reference Earle and Eells6]. In particular, the generator is unique for S 2 as seen in
$\pi_1(\operatorname{Diff}(S),\operatorname{id})$ is non-trivial [Reference Earle and Eells6]. In particular, the generator is unique for S 2 as seen in ![]() $\S$5.2.
$\S$5.2.
Given a punctured handlebody ![]() $H_{g,n}$, we indicate the index of a handle in the superscript and enumerate handles of each index in the subscript as follows:
$H_{g,n}$, we indicate the index of a handle in the superscript and enumerate handles of each index in the subscript as follows:
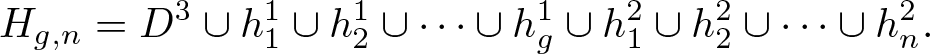 \begin{equation*}H_{g,n}=D^3\cup h^1_1\cup h^1_2\cup\dots\cup h^1_g\cup h^2_1\cup h^2_2\cup\dots\cup h^2_n.\end{equation*}
\begin{equation*}H_{g,n}=D^3\cup h^1_1\cup h^1_2\cup\dots\cup h^1_g\cup h^2_1\cup h^2_2\cup\dots\cup h^2_n.\end{equation*}Definition 6.1. Let n > 0, and let Sj be a properly embedded sphere in ![]() $H_{g,n}$ parallel to the boundary of
$H_{g,n}$ parallel to the boundary of  $D^3\cup h^2_j\subset H_{g,n}$ for each
$D^3\cup h^2_j\subset H_{g,n}$ for each ![]() $j=1,\dots,n$. A twist along Sj is called a sphere twist and is denoted by σ j.
$j=1,\dots,n$. A twist along Sj is called a sphere twist and is denoted by σ j.
A sphere twist σ j changes the framing of the cocore of the j-th 2-handle while fixing the cocore as shown in Figure 20. When n = 1, we simply denote a sphere twist on the handlebody with one puncture by σ.
Definition 6.2. Let ![]() $g,n \gt 0$ and let
$g,n \gt 0$ and let ![]() $T^j_l$ be a properly embedded torus in
$T^j_l$ be a properly embedded torus in ![]() $H_{g,n}$ parallel to the boundary of
$H_{g,n}$ parallel to the boundary of  $D^3\cup h^1_l\cup h^2_j\subset H_{g,n}$ for each
$D^3\cup h^1_l\cup h^2_j\subset H_{g,n}$ for each ![]() $l=1,\dots,g$ and
$l=1,\dots,g$ and ![]() $j=1,\dots,n$. A twist along
$j=1,\dots,n$. A twist along ![]() $T^j_l$ is called a torus twist and is denoted by
$T^j_l$ is called a torus twist and is denoted by ![]() $\tau^j_l$.
$\tau^j_l$.
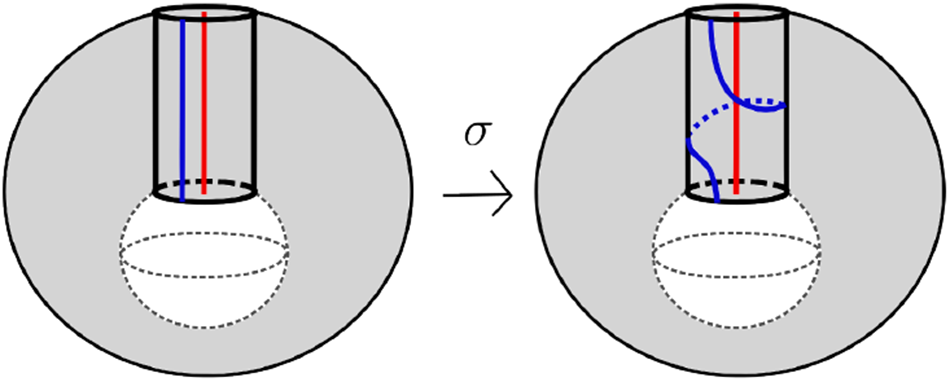
Figure 20. A sphere twist on the punctured ball ![]() $H_{0,1}$.
$H_{0,1}$.
A torus twist ![]() $\tau^j_l$ pushes the puncture inside
$\tau^j_l$ pushes the puncture inside  $D^3\cup H^2_j\subset H_{g,n}$ around the l-th 1-handle and back to its starting position, or equivalently, it sends the cocore of the j-th 2-handle to an arc in
$D^3\cup H^2_j\subset H_{g,n}$ around the l-th 1-handle and back to its starting position, or equivalently, it sends the cocore of the j-th 2-handle to an arc in ![]() $H_{g,n}$ running through the l-th 1-handle. Similarly, let τ denote a torus twist when
$H_{g,n}$ running through the l-th 1-handle. Similarly, let τ denote a torus twist when ![]() $g=n=1$.
$g=n=1$.
Composing two torus twists (Figure 21) pushes the puncture around the 1-handle twice, and thus the cocore of the 2-handle gets mapped to an arc running through the 1-handle twice and so on.
Example 6.3. The composition of torus twists ![]() $\tau^1_2\circ\tau^2_2\colon H_{2,2}\rightarrow H_{2,2}$ sends the cocore of the second 2-handle to an arc running through the second 1-handle and sends the cocore of the first 2-handle to an arc also running through the second 1-handle as demonstrated in Figure 22.
$\tau^1_2\circ\tau^2_2\colon H_{2,2}\rightarrow H_{2,2}$ sends the cocore of the second 2-handle to an arc running through the second 1-handle and sends the cocore of the first 2-handle to an arc also running through the second 1-handle as demonstrated in Figure 22.

Figure 21. Torus twist on the punctured solid torus ![]() $H_{1,1}$.
$H_{1,1}$.
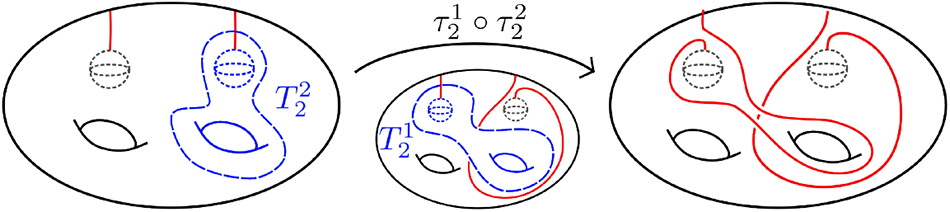
Figure 22. A twist along ![]() $T^2_2$ followed by a twist along
$T^2_2$ followed by a twist along ![]() $T^1_2$.
$T^1_2$.
6.2. An example
We apply Algorithm 4.4 step-by-step with inputs:
• a Heegaard diagram of the punctured solid torus
 $H_{1,1}$ as in Figure 2 and
$H_{1,1}$ as in Figure 2 and• image under
 $\sigma\circ\tau\circ\tau\circ\tau$ of the 2-handle. (Figure 23 only shows the image of the cocore of the 2-handle.)
$\sigma\circ\tau\circ\tau\circ\tau$ of the 2-handle. (Figure 23 only shows the image of the cocore of the 2-handle.)
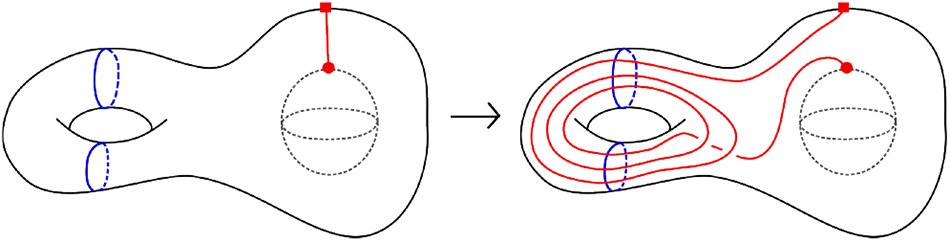
Figure 23. A composition of three torus twists.
Step 1: Use Algorithm 3.7 to get a Kirby diagram of the half open book with page ![]() $H_{1,1}$, which consists of a pair of D 3s and an unknot with blackboard framing in the yz-plane in
$H_{1,1}$, which consists of a pair of D 3s and an unknot with blackboard framing in the yz-plane in ![]() $\mathbb{R}^3$. Step 2: Add behind the yz-plane a half-meridian with blackboard framing to the unknot. Step 3: Add in front of the yz-plane a half-meridian with blackboard framing to the unknot and replace it with its image under
$\mathbb{R}^3$. Step 2: Add behind the yz-plane a half-meridian with blackboard framing to the unknot. Step 3: Add in front of the yz-plane a half-meridian with blackboard framing to the unknot and replace it with its image under ![]() $\sigma\circ\tau\circ\tau\circ\tau$. In Figure 23, the pair of circles (blue) on the torus each bound a disc, which then bounds a solid cylinder inside
$\sigma\circ\tau\circ\tau\circ\tau$. In Figure 23, the pair of circles (blue) on the torus each bound a disc, which then bounds a solid cylinder inside ![]() $H_{1,1}$. This solid cylinder corresponds to the 1-handle as seen in Figure 2. Observe that the cocore of the 2-handle (red) gets mapped to an arc running through the 1-handle three times. Thus, the image of the half-meridian is an arc running through D 3 thrice. Since the monodromy contains a sphere twist, the image of a parallel arc of the cocore twists once along the image of the cocore.
$H_{1,1}$. This solid cylinder corresponds to the 1-handle as seen in Figure 2. Observe that the cocore of the 2-handle (red) gets mapped to an arc running through the 1-handle three times. Thus, the image of the half-meridian is an arc running through D 3 thrice. Since the monodromy contains a sphere twist, the image of a parallel arc of the cocore twists once along the image of the cocore.
6.3. Equivalence of Kirby diagrams
When going from the middle to the right in Figure 24, one could have also obtained any Kirby diagram shown in Figure 25. The fact that these Kirby diagrams represent diffeomorphic manifolds will be useful when it comes to proving Corollaries 7.3 and 7.4.
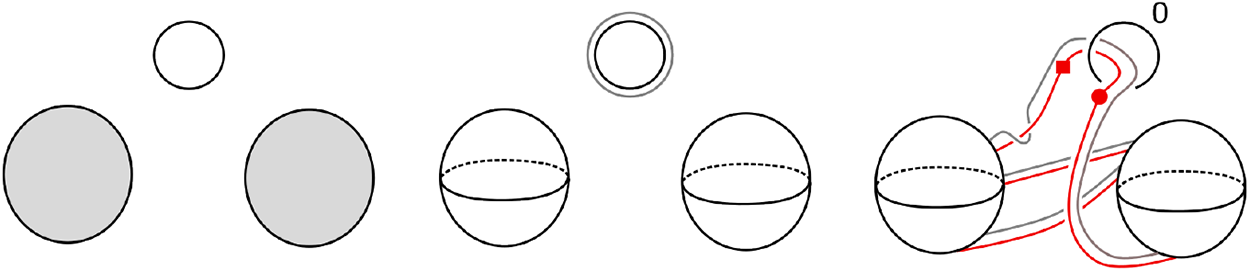
Figure 24. Left to right: a Heegaard diagram of ![]() $H_{1,1}$, a Kirby diagram of half open book and a Kirby diagram of
$H_{1,1}$, a Kirby diagram of half open book and a Kirby diagram of ![]() $\operatorname{Ob}(H_{1,1},\sigma\circ\tau\circ\tau\circ\tau)$.
$\operatorname{Ob}(H_{1,1},\sigma\circ\tau\circ\tau\circ\tau)$.
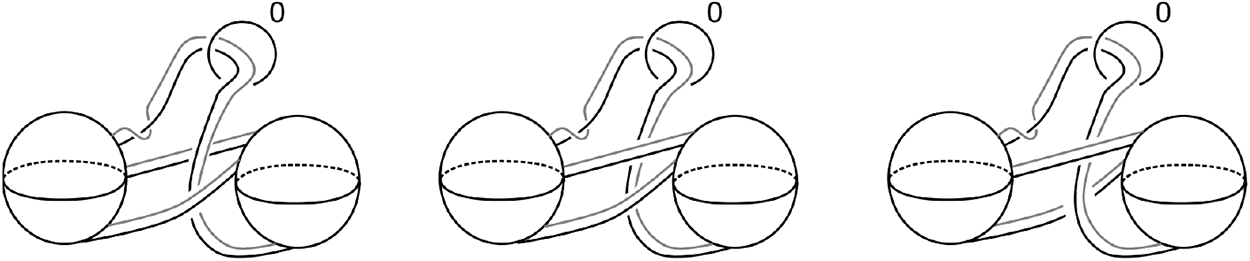
Figure 25. Some other Kirby diagrams of ![]() $\operatorname{Ob}(H_{1,1},\sigma\circ\tau\circ\tau\circ\tau)$.
$\operatorname{Ob}(H_{1,1},\sigma\circ\tau\circ\tau\circ\tau)$.
It suffices to show that the family of diagrams in Figure 26 are equivalent.
Definition 6.4. A Kirby diagram is said to come from a p-braid if it is a Kirby diagram obtained from a p-stranded braid, or p-braid for short, by
• embedding the braid in the thickened yz-plane in
 $\mathbb{R}^3$,
$\mathbb{R}^3$,• closing it off by attaching a pair of identified D 3s,
• adding blackboard framing and
• adding a 0-framed meridian.
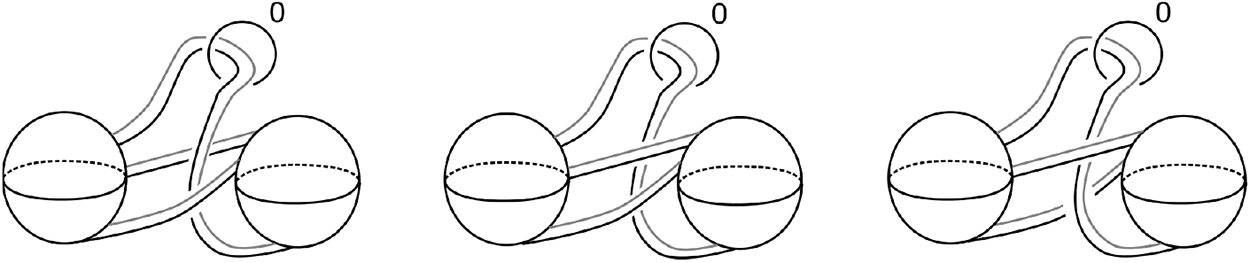
Figure 26. Some Kirby diagrams of ![]() $\operatorname{Ob}(H_{1,1},\tau\circ\tau\circ\tau)$.
$\operatorname{Ob}(H_{1,1},\tau\circ\tau\circ\tau)$.
We are interested in Kirby diagrams that come from a p-braid whose closure is a knot (for example Figure 27). Lemma 6.5 implies that the Kirby diagrams in Figure 26 represent diffeomorphic 4-manifolds.
Lemma 6.5. All Kirby diagrams that come from a p-braid whose closure is a knot represent diffeomorphic 4-manifolds.
Proof. A p-braid induces a permutation on p letters. First claim: p-braids that induce the same permutation on p letters give rise to Kirby diagrams representing diffeomorphic 4-manifolds. If two non-equivalent p-braids induce the same permutation on p letters, then they are related by crossing changes. By isotopy, move the 0-framed meridian close to a crossing and then slide the 2-handle over it to change the crossing as shown in Figure 28. Note that the framing of both 2-handles remains unchanged. The handle slide is a Kirby diagram invariant move, hence proving the first claim. Consequently, a permutation on p letters defines a Kirby diagram.
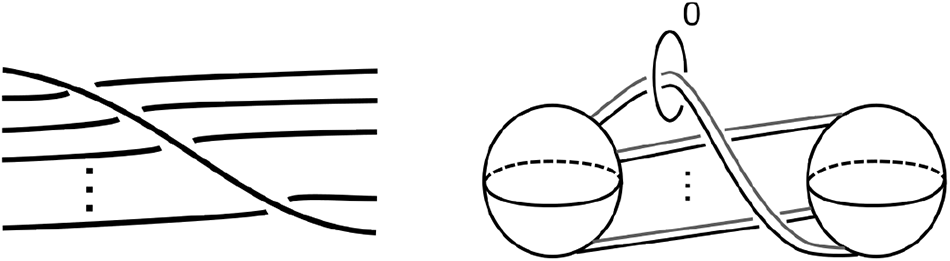
Figure 27. A Kirby diagram coming from a braid whose closure is a knot.
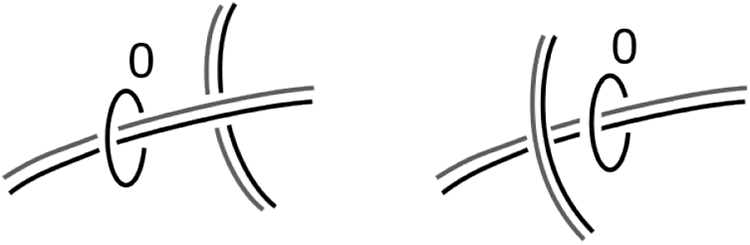
Figure 28. A handle slide changes the crossing.
Second claim: permutations up to conjugation by a cycle of length two give rise to Kirby diagrams representing diffeomorphic 4-manifolds. Isotope the 2-handle that intersects with the attaching region D 3 along ![]() $\partial D^3$. We can switch the places of two intersections without changing the framing of the 2-handle as shown in Figure 29(a). This Kirby diagram isotopy corresponds to adding a conjugate pair of braids to each end of a braid as shown in Figure 29(b) or equivalently to conjugating the induced permutation by a cycle of length two. This proves the second claim.
$\partial D^3$. We can switch the places of two intersections without changing the framing of the 2-handle as shown in Figure 29(a). This Kirby diagram isotopy corresponds to adding a conjugate pair of braids to each end of a braid as shown in Figure 29(b) or equivalently to conjugating the induced permutation by a cycle of length two. This proves the second claim.
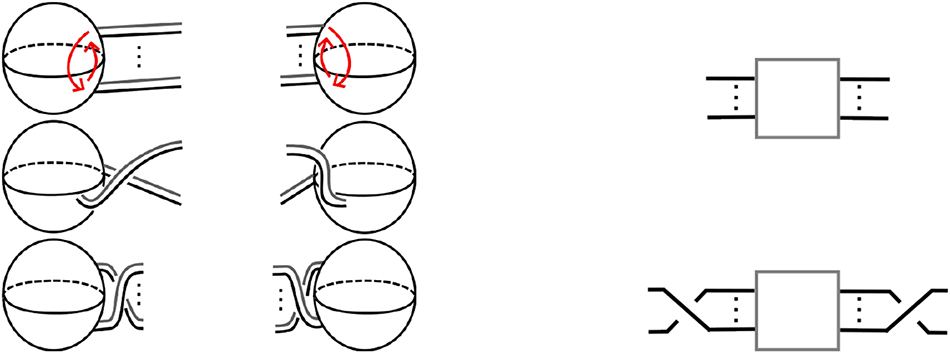
Figure 29. Isotoping the 2-handle along the boundary of the ![]() $D^3$ switching the places of two intersections corresponds to adding a conjugate pair of braids.
$D^3$ switching the places of two intersections corresponds to adding a conjugate pair of braids.
On one hand, if two p-braids induce the same permutation, then we are done by the first claim. On the other hand, if two p-braids induce different permutations, then p > 1. A p-braid whose closure is a knot induces a permutation with no fixed points that can be represented by a cycle ![]() $(a_1a_2\dots a_p)$ of length p. According to the following computation, for i ≠ j,
$(a_1a_2\dots a_p)$ of length p. According to the following computation, for i ≠ j,
permutations on p letters with no fixed points are all equivalent up to conjugations by a cycle of length two. The proof is complete by the second claim.
7. Applications
One can perturb a Kirby diagram of a 4-dimensional open book with trivial monodromy in such a way that one recognizes a different open book decomposition of the same 4-manifold as demonstrated in Figure 30. For example, it follows that ![]() $\operatorname{Ob}(\operatorname{L}(3,1)-D^3,\operatorname{id})$ is diffeomorphic to
$\operatorname{Ob}(\operatorname{L}(3,1)-D^3,\operatorname{id})$ is diffeomorphic to ![]() $\operatorname{Ob}(H_{1,1},\sigma\circ\tau\circ\tau\circ\tau)$. With this observation and Proposition 7.1, we prove that any open book constructed with trivial monodromy admits an open book decomposition with a punctured handlebody as page. Corollary 7.4 shows that the spin of a lens space
$\operatorname{Ob}(H_{1,1},\sigma\circ\tau\circ\tau\circ\tau)$. With this observation and Proposition 7.1, we prove that any open book constructed with trivial monodromy admits an open book decomposition with a punctured handlebody as page. Corollary 7.4 shows that the spin of a lens space ![]() $\operatorname{L}(p,q)$ only depends on p [Reference Meier18, Reference Pao22, Reference Plotnick23].
$\operatorname{L}(p,q)$ only depends on p [Reference Meier18, Reference Pao22, Reference Plotnick23].
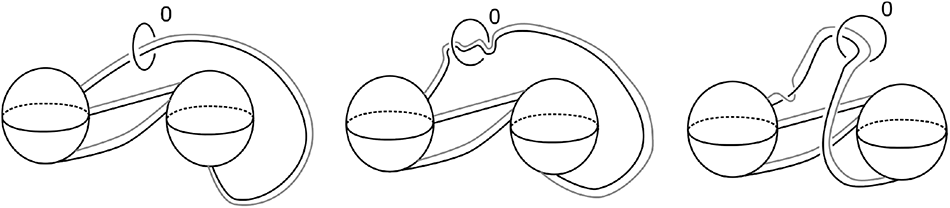
Figure 30. Left to right: Perturb the Kirby diagram by rotating the 0-framed meridian from a position transverse to the paper to lay down on the paper. We have encountered the Kirby diagram on the left in Figure 18, which is a Kirby diagram of ![]() $\operatorname{Ob}(\operatorname{L}(3,1)-D^3,\operatorname{id})$. The Kirby diagram on the right represents
$\operatorname{Ob}(\operatorname{L}(3,1)-D^3,\operatorname{id})$. The Kirby diagram on the right represents ![]() $\operatorname{Ob}(H_{1,1},\sigma\circ\tau\circ\tau\circ\tau)$ as seen in Figure 24.
$\operatorname{Ob}(H_{1,1},\sigma\circ\tau\circ\tau\circ\tau)$ as seen in Figure 24.
The following proposition delivers the existence of a desired monodromy for Theorem 7.2.
Proposition 7.1. Given ![]() $g,n \gt 0$. There exists a monodromy on
$g,n \gt 0$. There exists a monodromy on ![]() $H_{g,n}$ that sends the cocore of the j-th 2-handle to an arc in
$H_{g,n}$ that sends the cocore of the j-th 2-handle to an arc in ![]() $H_{g,n}$ running through the 1-handles
$H_{g,n}$ running through the 1-handles
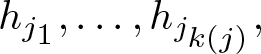 \begin{equation*}h_{j_1},\dots,h_{j_{k(j)}},\end{equation*}
\begin{equation*}h_{j_1},\dots,h_{j_{k(j)}},\end{equation*} where ![]() $\{j_1,\dots,j_{k(j)}\}\subset\{0,1,\dots,g\}$, for all
$\{j_1,\dots,j_{k(j)}\}\subset\{0,1,\dots,g\}$, for all ![]() $j=1,\dots,n$.
$j=1,\dots,n$.
Proof. It follows by Definition 6.2 that
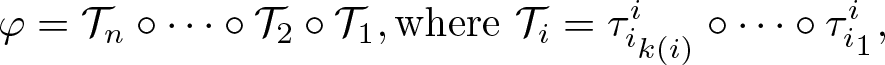 \begin{equation*}\varphi=\mathcal{T}_n\circ\dots\circ\mathcal{T}_2\circ\mathcal{T}_1,\text{where }\mathcal{T}_i=\tau^i_{i_{k(i)}}\circ\dots\circ\tau^i_{i_1},\end{equation*}
\begin{equation*}\varphi=\mathcal{T}_n\circ\dots\circ\mathcal{T}_2\circ\mathcal{T}_1,\text{where }\mathcal{T}_i=\tau^i_{i_{k(i)}}\circ\dots\circ\tau^i_{i_1},\end{equation*} for all ![]() $i=1,\dots,n$, is a monodromy on
$i=1,\dots,n$, is a monodromy on ![]() $H_{g,n}$ that sends the cocore of the j-th 2-handle to an arc in
$H_{g,n}$ that sends the cocore of the j-th 2-handle to an arc in ![]() $H_{g,n}$ running through the 1-handles
$H_{g,n}$ running through the 1-handles
 \begin{equation*}h_{j_1},\dots,h_{j_{k(j)}}\end{equation*}
\begin{equation*}h_{j_1},\dots,h_{j_{k(j)}}\end{equation*} for all ![]() $j=1,\dots,n$.
$j=1,\dots,n$.
Theorem 7.2. Given any compact oriented 3-manifold M with a non-empty boundary, there exists a monodromy φ on a punctured handlebody H such that ![]() $\operatorname{Ob}(H,\varphi)$ is diffeomorphic to
$\operatorname{Ob}(H,\varphi)$ is diffeomorphic to ![]() $\operatorname{Ob}(M,\operatorname{id})$. Furthermore, suppose M admits a handle decomposition with a single 0-handle, g 1-handles and n 2-handles, then
$\operatorname{Ob}(M,\operatorname{id})$. Furthermore, suppose M admits a handle decomposition with a single 0-handle, g 1-handles and n 2-handles, then ![]() $H=H_{g,n}$ and φ is given by a composition of sphere twists and torus twists, namely, a torus twist
$H=H_{g,n}$ and φ is given by a composition of sphere twists and torus twists, namely, a torus twist ![]() $\tau^j_l$ each time the attaching sphere of the j-th 2-handle runs through the l-th 1-handle in M.
$\tau^j_l$ each time the attaching sphere of the j-th 2-handle runs through the l-th 1-handle in M.
Proof. Suppose M is not a punctured handlebody, otherwise, just take H = M and the theorem is trivial. Given a Heegaard diagram of M that came from a standard handle decomposition without 3-handles, with n 2-handles (note that n > 0, since n = 0 would imply that M is a handlebody) and g 1-handles, Algorithm 3.7 produces a Kirby diagram of the half open book with page M that consists of n blackboard-framed 2-handle attaching spheres ![]() $\alpha_1,\dots,\alpha_n$ and g pairs of D 3s. According to Algorithm 4.1, adding a 0-framed meridian βi to each αi gives a Kirby diagram of the open book
$\alpha_1,\dots,\alpha_n$ and g pairs of D 3s. According to Algorithm 4.1, adding a 0-framed meridian βi to each αi gives a Kirby diagram of the open book ![]() $\operatorname{Ob}(M,\operatorname{id})$. Note that αi lies in the yz-plane and βi is transverse to the yz-plane for all
$\operatorname{Ob}(M,\operatorname{id})$. Note that αi lies in the yz-plane and βi is transverse to the yz-plane for all ![]() $i=1,\dots,n$. We will perturb this Kirby diagram of
$i=1,\dots,n$. We will perturb this Kirby diagram of ![]() $\operatorname{Ob}(M,\operatorname{id})$ to a Kirby diagram of
$\operatorname{Ob}(M,\operatorname{id})$ to a Kirby diagram of ![]() $\operatorname{Ob}(H_{g,n},\varphi)$, for some monodromy
$\operatorname{Ob}(H_{g,n},\varphi)$, for some monodromy ![]() $\varphi\colon H_{g,n}\rightarrow H_{g,n}$ given by a composition of twists along spheres and tori embedded in
$\varphi\colon H_{g,n}\rightarrow H_{g,n}$ given by a composition of twists along spheres and tori embedded in ![]() $H_{g,n}$.
$H_{g,n}$.
Perturb this Kirby diagram of ![]() $\operatorname{Ob}(M,\operatorname{id})$ so that each meridian βi becomes an unknot in the yz-plane. As a result, two small intervals of the 2-handle attaching sphere αi,
$\operatorname{Ob}(M,\operatorname{id})$ so that each meridian βi becomes an unknot in the yz-plane. As a result, two small intervals of the 2-handle attaching sphere αi, ![]() $i=1,\dots,n$, are forced to leave the yz-plane as shown in Figure 31. The perturbed Kirby diagram of
$i=1,\dots,n$, are forced to leave the yz-plane as shown in Figure 31. The perturbed Kirby diagram of ![]() $\operatorname{Ob}(M,\operatorname{id})$ still represents the same 4-manifold. We would like to consider the perturbed Kirby diagram as the union of αi,
$\operatorname{Ob}(M,\operatorname{id})$ still represents the same 4-manifold. We would like to consider the perturbed Kirby diagram as the union of αi, ![]() $i=1,\dots,n$ and a Kirby diagram of some half open book X. We remove all the αis from the perturbed Kirby diagram and refer to the resulting Kirby diagram as X. To see the page of the half open book X, we perform Algorithm 3.7 in a reversed manner: remove the framing coefficients of the 2-handle attaching spheres in X and replace all D 3s with D 2s. This leaves us with n unknots and g pairs of D 2s in the yz-plane, which is a Heegaard diagram of the punctured handlebody
$i=1,\dots,n$ and a Kirby diagram of some half open book X. We remove all the αis from the perturbed Kirby diagram and refer to the resulting Kirby diagram as X. To see the page of the half open book X, we perform Algorithm 3.7 in a reversed manner: remove the framing coefficients of the 2-handle attaching spheres in X and replace all D 3s with D 2s. This leaves us with n unknots and g pairs of D 2s in the yz-plane, which is a Heegaard diagram of the punctured handlebody ![]() $H_{g,n}$. Hence, the perturbed Kirby diagram of
$H_{g,n}$. Hence, the perturbed Kirby diagram of ![]() $\operatorname{Ob}(M,\operatorname{id})$ is the union of the framed 2-handle attaching spheres
$\operatorname{Ob}(M,\operatorname{id})$ is the union of the framed 2-handle attaching spheres ![]() $\alpha_1,\dots,\alpha_n$ and a Kirby diagram of the half open book with page
$\alpha_1,\dots,\alpha_n$ and a Kirby diagram of the half open book with page ![]() $H_{g,n}$. It remains to show the existence of a monodromy
$H_{g,n}$. It remains to show the existence of a monodromy ![]() $\varphi\colon H_{g,n}\rightarrow H_{g,n}$ such that the Kirby diagram of
$\varphi\colon H_{g,n}\rightarrow H_{g,n}$ such that the Kirby diagram of ![]() $\operatorname{Ob}(H_{g,n},\operatorname{\varphi})$ is given by adding αi,
$\operatorname{Ob}(H_{g,n},\operatorname{\varphi})$ is given by adding αi, ![]() $i=1,\dots,n$, to X.
$i=1,\dots,n$, to X.
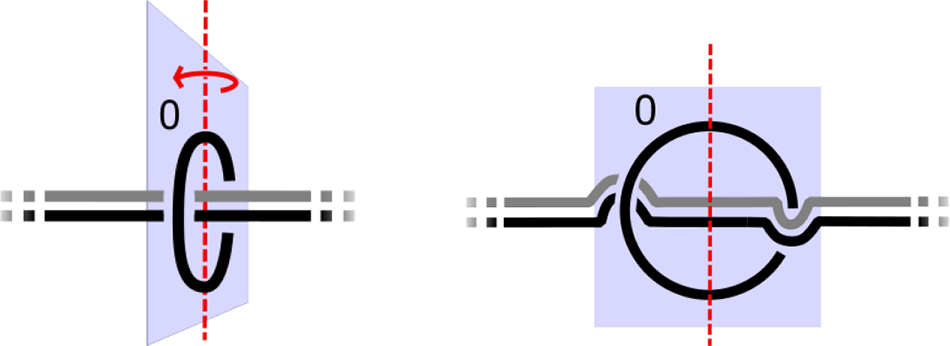
Figure 31. Rotate about the dashed line (red) so that the 0-framed meridian lies on the yz-plane. This forces two small intervals of ![]() $\alpha_i$ to leave the yz-plane.
$\alpha_i$ to leave the yz-plane.
Let us see what properties the desired φ must satisfy by analysing our target, the perturbed Kirby diagram of ![]() $\operatorname{Ob}(M,\operatorname{id})$.
$\operatorname{Ob}(M,\operatorname{id})$.
• The framed arc that is immersed behind the yz-plane would be the image of the attaching sphere in the back cover of the half open book with page
 $H_{g,n}$. (Recall Step 2 of Algorithm 4.4: add behind the yz-plane a half-meridian with blackboard framing.)
$H_{g,n}$. (Recall Step 2 of Algorithm 4.4: add behind the yz-plane a half-meridian with blackboard framing.)• The framed arc that popped out of the yz-plane together with the rest of that framed 2-handle attaching sphere in the yz-plane would be the image of the attaching sphere in the front cover of the half open book. (Recall the part of a Kirby diagram in front of the yz-plane is identified with the front cover of the half open book with page
 $H_{g,n}$.)
$H_{g,n}$.)
Suppose αj runs through the 1-handles  $h_{j_1},h_{j_2},\dots,h_{j_{k(j)}}$, possibly with multiplicity, then the desired monodromy φ must send the cocore of the j-th 2-handle to an arc in
$h_{j_1},h_{j_2},\dots,h_{j_{k(j)}}$, possibly with multiplicity, then the desired monodromy φ must send the cocore of the j-th 2-handle to an arc in ![]() $H_{g,n}$ running through the 1-handles
$H_{g,n}$ running through the 1-handles  $h_{j_1},h_{j_2},\dots,h_{j_{k(j)}}$ for all
$h_{j_1},h_{j_2},\dots,h_{j_{k(j)}}$ for all ![]() $j=1,\dots,n$. There exists such a monodromy by Proposition 7.1, namely,
$j=1,\dots,n$. There exists such a monodromy by Proposition 7.1, namely,
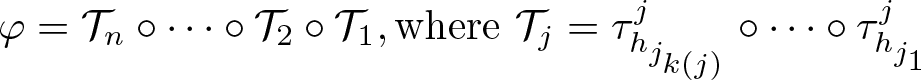 \begin{equation*}\varphi=\mathcal{T}_n\circ\dots\circ\mathcal{T}_2\circ\mathcal{T}_1,\text{where }\mathcal{T}_j=\tau^j_{h_{j_{k(j)}}}\circ\dots\circ\tau^j_{h_{j_1}}\end{equation*}
\begin{equation*}\varphi=\mathcal{T}_n\circ\dots\circ\mathcal{T}_2\circ\mathcal{T}_1,\text{where }\mathcal{T}_j=\tau^j_{h_{j_{k(j)}}}\circ\dots\circ\tau^j_{h_{j_1}}\end{equation*} for all ![]() $j=1,\dots,n$. (If αl does not run through any D 3s in the Kirby diagram of
$j=1,\dots,n$. (If αl does not run through any D 3s in the Kirby diagram of ![]() $\operatorname{Ob}(M,\operatorname{id})$, then
$\operatorname{Ob}(M,\operatorname{id})$, then ![]() $\mathcal{T}_l$ is just the identity map. This cannot be the case for all
$\mathcal{T}_l$ is just the identity map. This cannot be the case for all ![]() $l\in\{1,\dots,n\}$ because M is by assumption, not a punctured handlebody.) Compose φ with a composition of sphere twists σ j to correct the framing of the image of αj,
$l\in\{1,\dots,n\}$ because M is by assumption, not a punctured handlebody.) Compose φ with a composition of sphere twists σ j to correct the framing of the image of αj, ![]() $j=1,\dots,n$, if necessary.
$j=1,\dots,n$, if necessary.
Corollary 7.3. Every spun lens space is an open book with the punctured solid torus ![]() $H_{1,1}$ as page. More specifically,
$H_{1,1}$ as page. More specifically, ![]() $\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\operatorname{id})$ is diffeomorphic to
$\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\operatorname{id})$ is diffeomorphic to ![]() $\operatorname{Ob}(H_{1,1},(\sigma)^q\circ(\tau)^p)$, where
$\operatorname{Ob}(H_{1,1},(\sigma)^q\circ(\tau)^p)$, where ![]() $(\sigma)^q\circ(\tau)^p$ denotes a composition of p torus twists and q sphere twists.
$(\sigma)^q\circ(\tau)^p$ denotes a composition of p torus twists and q sphere twists.
Proof. It follows Algorithm 4.4 that a Kirby diagram coming from a p-braid, whose closure is a knot, is a Kirby diagram of ![]() $\operatorname{Ob}(H_{1,1},(\tau)^p)$. By Lemma 6.5, we may consider the p-braid given in Figure 32(c). One can check that the braid in Figure 32(c) is equivalent to the product of q copies of the braid in Figure 32(a).
$\operatorname{Ob}(H_{1,1},(\tau)^p)$. By Lemma 6.5, we may consider the p-braid given in Figure 32(c). One can check that the braid in Figure 32(c) is equivalent to the product of q copies of the braid in Figure 32(a).
To get a Kirby diagram of ![]() $\operatorname{Ob}(H_{1,1},(\sigma)^q\circ(\tau)^p)$, we simply add q twists to the parallel knot as shown in Figure 33.
$\operatorname{Ob}(H_{1,1},(\sigma)^q\circ(\tau)^p)$, we simply add q twists to the parallel knot as shown in Figure 33.
The braid has been chosen so that the Kirby diagram in Figure 33 can be isotoped to a Kirby diagram of the spun lens space ![]() $\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\operatorname{id})$ as in Figure 17 by pulling the q over-strands outwards. This shows that
$\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\operatorname{id})$ as in Figure 17 by pulling the q over-strands outwards. This shows that ![]() $\operatorname{Ob}(H_{1,1},(\sigma)^q\circ(\tau)^p)$ is diffeomorphic to
$\operatorname{Ob}(H_{1,1},(\sigma)^q\circ(\tau)^p)$ is diffeomorphic to ![]() $\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\operatorname{id})$.
$\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\operatorname{id})$.
The case ![]() $(p,q)=(5,4)$ is demonstrated in Figure 34.
$(p,q)=(5,4)$ is demonstrated in Figure 34.
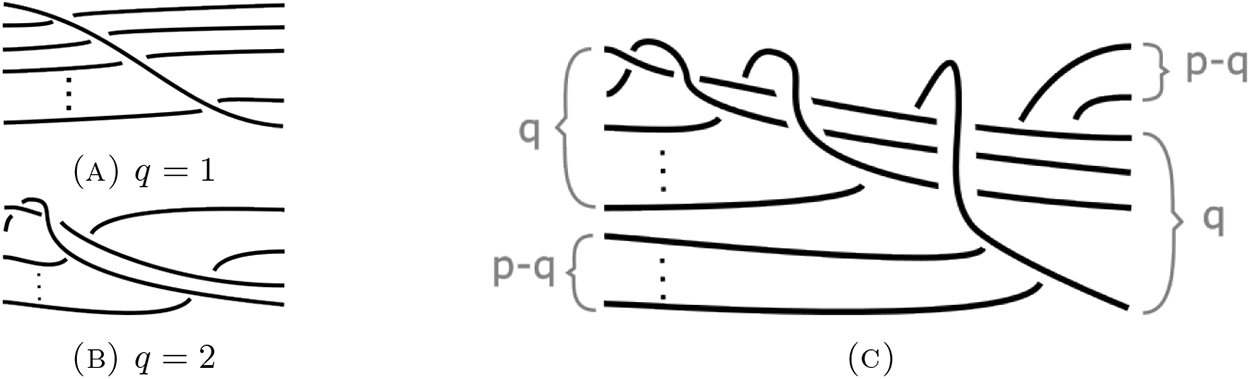
Figure 32. A family of p-braids whose closure are knots.
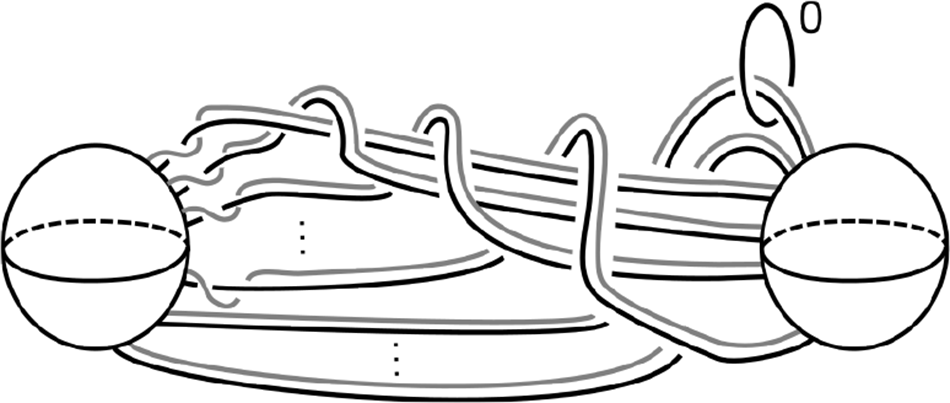
Figure 33. A Kirby diagram of ![]() $\operatorname{Ob}(H_{1,1},(\sigma)^q\circ(\tau)^p)$.
$\operatorname{Ob}(H_{1,1},(\sigma)^q\circ(\tau)^p)$.
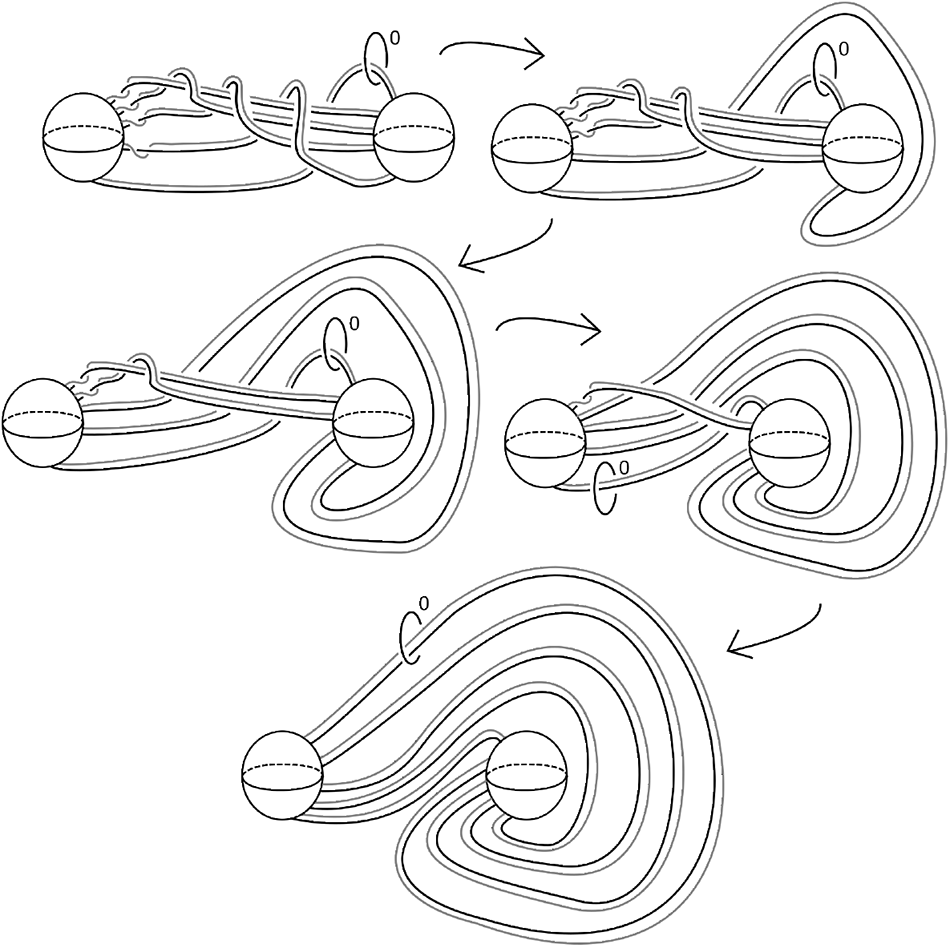
Figure 34. ![]() $\operatorname{Ob}(H_{1,1},(\sigma)^4\circ(\tau)^5)$ is diffeomorphic to
$\operatorname{Ob}(H_{1,1},(\sigma)^4\circ(\tau)^5)$ is diffeomorphic to ![]() $\operatorname{Ob}(\operatorname{L}(5,4)-D^3,\operatorname{id})$.
$\operatorname{Ob}(\operatorname{L}(5,4)-D^3,\operatorname{id})$.
Corollary 7.4 is a particular case of Pao’s and Plotnick’s work [Reference Pao22, Reference Plotnick23], placed into context by Meier [Reference Meier18, Corollary 2.4]. We provide a Kirby calculus proof.
Corollary 7.4. For all ![]() $1 \leq q \lt p$, the diffeomorphism type of a spun lens space
$1 \leq q \lt p$, the diffeomorphism type of a spun lens space ![]() $\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\operatorname{id})$ is independent of q.
$\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\operatorname{id})$ is independent of q.
Proof. We first show that the diffeomorphism type of a spun lens space ![]() $\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\operatorname{id})$ is independent of the parity of q, for
$\operatorname{Ob}(\operatorname{L}(p,q)-D^3,\operatorname{id})$ is independent of the parity of q, for ![]() $q \lt 2p$.
$q \lt 2p$.
We will show that ![]() $\operatorname{Ob}(\operatorname{L}(p,2k)-D^3,\operatorname{id})$,
$\operatorname{Ob}(\operatorname{L}(p,2k)-D^3,\operatorname{id})$, ![]() $k\in\mathbb{N}$,
$k\in\mathbb{N}$, ![]() $p,2k$ coprime and
$p,2k$ coprime and ![]() $2k \lt 2p$ are diffeomorphic to each other. Similarly,
$2k \lt 2p$ are diffeomorphic to each other. Similarly, ![]() $\operatorname{Ob}(\operatorname{L}(p,2k+1)-D^3,\operatorname{id})$,
$\operatorname{Ob}(\operatorname{L}(p,2k+1)-D^3,\operatorname{id})$, ![]() $k\in\mathbb{N}$,
$k\in\mathbb{N}$, ![]() $p, 2k+1$ coprime and
$p, 2k+1$ coprime and ![]() $2k+1 \lt 2p$ are diffeomorphic to each other. The proof of the latter is essentially the same and hence omitted. See Figure 35.
$2k+1 \lt 2p$ are diffeomorphic to each other. The proof of the latter is essentially the same and hence omitted. See Figure 35.
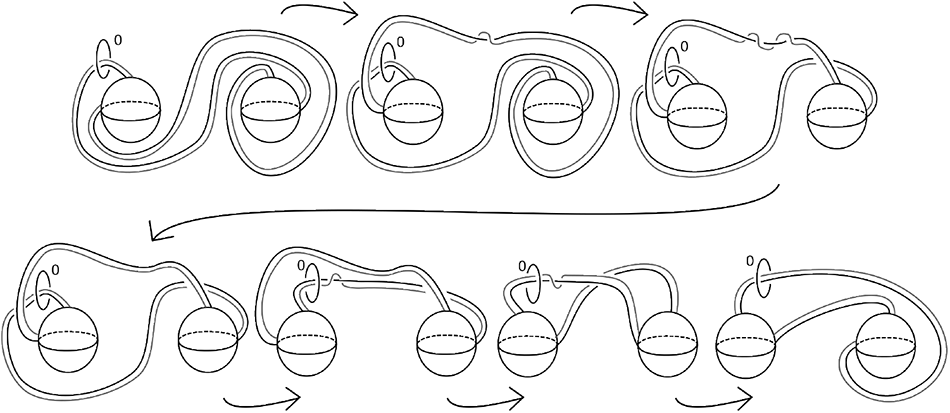
Figure 35. ![]() $\operatorname{Ob}(\operatorname{L}(2,3)-D^3,\operatorname{id})$ is diffeomorphic to
$\operatorname{Ob}(\operatorname{L}(2,3)-D^3,\operatorname{id})$ is diffeomorphic to ![]() $\operatorname{Ob}(\operatorname{L}(2,1)-D^3,\operatorname{id})$. To go from the first row to the second, slide the other 2-handle over the 0-framed meridian. In the middle of the second row, we rotate the pair of D 3.
$\operatorname{Ob}(\operatorname{L}(2,1)-D^3,\operatorname{id})$. To go from the first row to the second, slide the other 2-handle over the 0-framed meridian. In the middle of the second row, we rotate the pair of D 3.
When ![]() $p \gt 2k$, consider the Kirby diagram of
$p \gt 2k$, consider the Kirby diagram of ![]() $\operatorname{Ob}(\operatorname{L}(p,2k)-D^3,\operatorname{id})$ shown in Figure 17. There are 2k strands to the right of D 3 on the right-hand side; perform the isotopy shown in Figure 36(b) to each one of them.
$\operatorname{Ob}(\operatorname{L}(p,2k)-D^3,\operatorname{id})$ shown in Figure 17. There are 2k strands to the right of D 3 on the right-hand side; perform the isotopy shown in Figure 36(b) to each one of them.
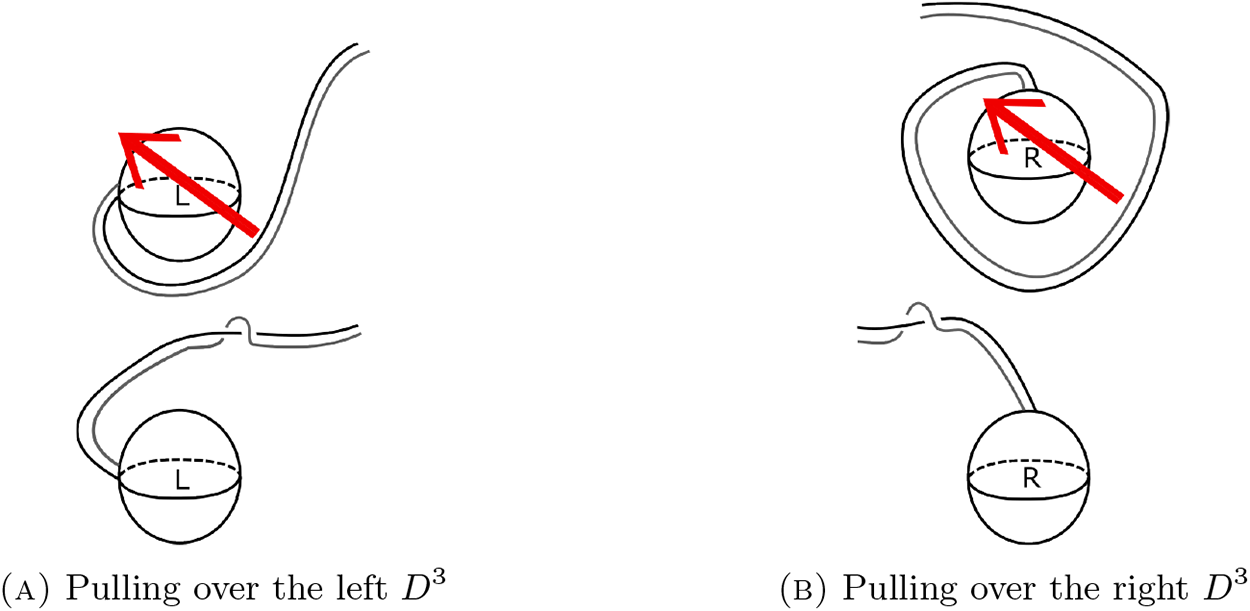
Figure 36.
As a result, the parallel knot gains 2k twists in total. Slide the 2-handle over the 0-framed meridian k times to undo these 2k twists restoring blackboard framing as shown in Figure 37. Hence, we have shown that a Kirby diagram of ![]() $\operatorname{Ob}(\operatorname{L}(p,2k)-D^3,\operatorname{id})$ and a Kirby diagram that comes from a p-braid whose closure is a knot represent diffeomorphic 4-manifolds for each integer
$\operatorname{Ob}(\operatorname{L}(p,2k)-D^3,\operatorname{id})$ and a Kirby diagram that comes from a p-braid whose closure is a knot represent diffeomorphic 4-manifolds for each integer ![]() $2k \lt p$ coprime with p.
$2k \lt p$ coprime with p.
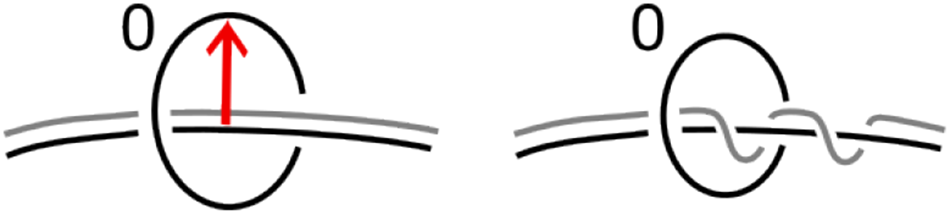
Figure 37. Slide the blackboard-framed 2-handle over the 0-framed meridian to change the framing by two.
When ![]() $p \lt 2k \lt 2p$, construct a Kirby diagram of
$p \lt 2k \lt 2p$, construct a Kirby diagram of ![]() $\operatorname{Ob}(\operatorname{L}(p,2k)-D^3,\operatorname{id})$ with Algorithm 4.1 using the Heegaard diagram in Figure 38 as input.
$\operatorname{Ob}(\operatorname{L}(p,2k)-D^3,\operatorname{id})$ with Algorithm 4.1 using the Heegaard diagram in Figure 38 as input.
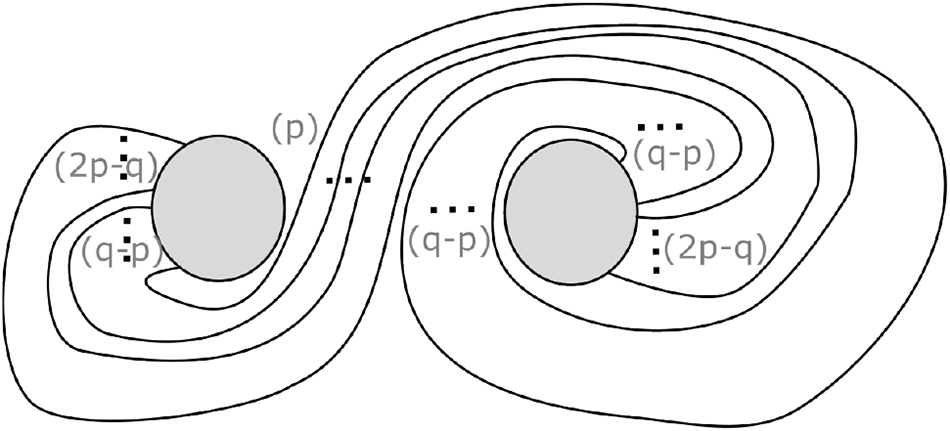
Figure 38. A Heegaard diagram of ![]() $\operatorname{L}(p,q)$, where
$\operatorname{L}(p,q)$, where ![]() $p \lt q \lt 2p$ and
$p \lt q \lt 2p$ and ![]() $p,q$ coprime. The attaching sphere of the 2-handle travels around the D 2 q times and runs through the 1-handle p times.
$p,q$ coprime. The attaching sphere of the 2-handle travels around the D 2 q times and runs through the 1-handle p times.
There are 2k strands between the centres of the D 3s, we free this space as follows: counting from the left, pull the first p strands (as in Figure 36(a)) over the left D 3 to the other side. There are also 2k strands to the right of the right D 3; counting from the right, pull the first ![]() $2k-p$ strands (as in Figure 36(b)) over the right D 3 to the other side.
$2k-p$ strands (as in Figure 36(b)) over the right D 3 to the other side.
As a result, the parallel knot gains 2k twists in total. We slide the blackboard-framed 2-handle over the 0-framed meridian k times to restore blackboard framing. Having cleaned up the space between the D 3s, we rotate a D 3 (the other D 3 rotates synchronously) so that a p-braid is formed in between the pair of D 3s. This shows that a Kirby diagram of ![]() $\operatorname{Ob}(\operatorname{L}(p,2k)-D^3,\operatorname{id})$ and a Kirby diagram that comes from a p-braid whose closure is a knot represent diffeomorphic 4-manifolds for each integer
$\operatorname{Ob}(\operatorname{L}(p,2k)-D^3,\operatorname{id})$ and a Kirby diagram that comes from a p-braid whose closure is a knot represent diffeomorphic 4-manifolds for each integer ![]() $2k\in (p,2p)$ coprime with p.
$2k\in (p,2p)$ coprime with p.
By Lemma 6.5, Kirby diagrams that come from a p-braid whose closure is a knot represent diffeomorphic 4-manifolds. Therefore, ![]() $\operatorname{Ob}(\operatorname{L}(p,2k)-D^3,\operatorname{id})$,
$\operatorname{Ob}(\operatorname{L}(p,2k)-D^3,\operatorname{id})$, ![]() $k\in\mathbb{N}$,
$k\in\mathbb{N}$, ![]() $p,2k$ coprime and
$p,2k$ coprime and ![]() $2k \lt 2p$, are diffeomorphic to each other.
$2k \lt 2p$, are diffeomorphic to each other.
Finally, by Rolfsen’s twist, ![]() $\operatorname{L}(p,q)$ is diffeomorphic to
$\operatorname{L}(p,q)$ is diffeomorphic to ![]() $\operatorname{L}(p,q+np)$ for all
$\operatorname{L}(p,q+np)$ for all ![]() $n\in\mathbb{N}$ [Reference Prasolov and Sossinsky24], thus
$n\in\mathbb{N}$ [Reference Prasolov and Sossinsky24], thus ![]() $\operatorname{L}(p,2k)$,
$\operatorname{L}(p,2k)$, ![]() $p \gt 2k$, is diffeomorphic to
$p \gt 2k$, is diffeomorphic to ![]() $\operatorname{L}(p,2k+p)$. By assumption, p and 2k are coprime, and hence
$\operatorname{L}(p,2k+p)$. By assumption, p and 2k are coprime, and hence ![]() $2k+p$ is odd. Since we have already established that the diffeomorphism type is independent of the parity of q, for
$2k+p$ is odd. Since we have already established that the diffeomorphism type is independent of the parity of q, for ![]() $q \lt 2p$, this completes the proof.
$q \lt 2p$, this completes the proof.
Acknowledgements
I am indebted to Marc Kegel, Felix Schmäschke and Thomas Vogel for helpful conversations. I would like to express my gratitude towards my advisor Marc Kegel for suggesting this topic to me and for his valuable mentoring which helped me to thrive for improvement. I am also grateful to Thomas Vogel for his encouragement. Finally, I would like to warmly thank Li-Chun Wang and give her credit for the 3D graphics in Figure 13.
The author is supported by the Claussen-Simon-Stiftung and the Berlin Mathematics Research Center MATH+ funded by the DFG (EXC-2046/1, ID 390685689).













































































