Article contents
Crystal flex bases and the RUM spectrum
Published online by Cambridge University Press: 24 November 2021
Abstract
A theory of infinite spanning sets and bases is developed for the first-order flex space of an infinite bar-joint framework, together with space group symmetric versions for a crystallographic bar-joint framework ${{\mathcal {C}}}$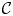 . The existence of a crystal flex basis for ${{\mathcal {C}}}$
. The existence of a crystal flex basis for ${{\mathcal {C}}}$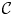 is shown to be closely related to the spectral analysis of the rigid unit mode (RUM) spectrum of ${{\mathcal {C}}}$
is shown to be closely related to the spectral analysis of the rigid unit mode (RUM) spectrum of ${{\mathcal {C}}}$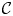 and an associated geometric flex spectrum. Additionally, infinite spanning sets and bases are computed for a range of fundamental crystallographic bar-joint frameworks, including the honeycomb (graphene) framework, the octahedron (perovskite) framework and the 2D and 3D kagome frameworks.
and an associated geometric flex spectrum. Additionally, infinite spanning sets and bases are computed for a range of fundamental crystallographic bar-joint frameworks, including the honeycomb (graphene) framework, the octahedron (perovskite) framework and the 2D and 3D kagome frameworks.
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 4 , November 2021 , pp. 735 - 761
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society
References
- 2
- Cited by


