No CrossRef data available.
Article contents
Conditions for Sylow 2-subgroups of the Fixed Point Subgroup Implying Solubility
Part of:
Representation theory of groups
Published online by Cambridge University Press: 25 September 2018
Abstract
Let A and G be finite groups and suppose that A acts via automorphisms on G with 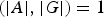 $(|A|, |G|)=1$. We study how certain conditions on the Sylow 2-subgroups of the fixed point subgroup of the action
$(|A|, |G|)=1$. We study how certain conditions on the Sylow 2-subgroups of the fixed point subgroup of the action 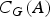 $C_G(A)$ may imply the non-simplicity or solubility of G.
$C_G(A)$ may imply the non-simplicity or solubility of G.
MSC classification
Secondary:
20D15: Nilpotent groups, $p$-groups
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 62 , Issue 1 , February 2019 , pp. 211 - 220
- Copyright
- Copyright © Edinburgh Mathematical Society 2018
References
1Beltrán, A., Invariant Sylow subgroups and solvability of finite groups, Arch. Math. 102(2) (2016), 101–106.Google Scholar
2Brauer, R. and Suzuki, M., On finite groups of even order whose 2-Sylow group is a quaternion group, Proc. Natl. Acad. Sci. USA 45 (1959), 1757–1759.Google Scholar
3Chen, Z. M. and Wang, Y. M., Minimal non-solvable groups with an acting group (in Chinese), Chin. Sci. Bull. 34(22) (1989), 1691–1693.Google Scholar
4Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A. Atlas of finite groups (Oxford University Press, London, 1985).Google Scholar
6Kurzweil, H. and Stellmacher, B., The theory of finite groups. An introduction (Springer-Verlag, Berlin–Heidelberg–New York, 2004).Google Scholar
7Walter, J. H., The characterization of finite groups with abelian Sylow 2-subgroups, Ann. Math. 89 (1969), 405–514.Google Scholar
8Walter, G. and Gorenstein, J. H., On finite groups with dihedral Sylow 2-subgroups, Illinois J. Math. 6 (1962), 553–593.Google Scholar

