Article contents
Completely bounded isomorphisms of injective von Neumann algebras
Published online by Cambridge University Press: 20 January 2009
Extract
Milutin's Theorem states that if X and Y are uncountable metrizable compact Hausdorff spaces, then C(X) and C(Y) are isomorphic as Banach spaces [15, p. 379]. Thus there is only one isomorphism class of such Banach spaces. There is also an extensive theory of the Banach–Mazur distance between various classes of classical Banach spaces with the deepest results depending on probabilistic and asymptotic estimates [18]. Lindenstrauss, Haagerup and possibly others know that as Banach spaces
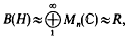
where H is the infinite dimensional separable Hilbert space, R is the injective II 1-factor on H, and ≈ denotes Banach space isomorphism. Haagerup informed us of this result, and suggested considering completely bounded isomorphisms; it is a pleasure to acknowledge his suggestion. We replace Banach space isomorphisms by completely bounded isomorphisms that preserve the linear structure and involution, but not the product. One of the two theorems of this paper is a strengthened version of the above result: if N is an injective von Neumann algebra with separable predual and not finite type I of bounded degree, then N is completely boundedly isomorphic to B(H). The methods used are similar to those in Banach space theory with complete boundedness needing a little care at various points in the argument. Extensive use is made of the conditional expectation available for injective algebras, and the methods do not apply to the interesting problems of completely bounded isomorphisms of non-injective von Neumann algebras (see [4] for a study of the completely bounded approximation property).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1989
References
REFERENCES
- 6
- Cited by

