Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kelevedjiev, P.
Popivanov, N.
and
Bekesheva, L.
2015.
Existence of solutions for a class of third-order nonlinear boundary value problem.
Vol. 1690,
Issue. ,
p.
040016.
Kelevedjiev, Petio
and
Todorov, Todor
2019.
Existence of solutions of nonlinear third-order two-point boundary value problems.
Electronic Journal of Qualitative Theory of Differential Equations,
p.
1.
Eloe, Paul
Henderson, Johnny
and
Neugebauer, Jeffrey
2020.
Three point boundary value problems for ordinary differential equations, uniqueness implies existence.
Electronic Journal of Qualitative Theory of Differential Equations,
p.
1.
Agarwal, Ravi P.
Bohner, Martin
and
Özbekler, Abdullah
2021.
Lyapunov Inequalities and Applications.
p.
133.
Eloe, Paul W.
and
Neugebauer, Dan
2022.
A global uniqueness of solutions implies global existence for (l+1)-point boundary value problems.
Rocky Mountain Journal of Mathematics,
Vol. 52,
Issue. 2,
Ma, Ruyun
and
Zhao, Jiao
2024.
Infinitely Many Nodal Solutions of Superlinear Third Order Two-Point Boundary Value Problems.
Results in Mathematics,
Vol. 79,
Issue. 3,
Mihaylova, G
and
Kelevedjiev, P
2025.
On the Solvability of a Two-Point Third-Order Boundary Value Problem Under Barrier Strips.
Proceedings of the Technical University of Sofia,
Vol. 74,
Issue. 3,


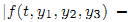
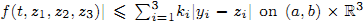 , questions involving ‘uniqueness implies uniqueness’, ‘uniqueness implies existence’ and ‘optimal length subintervals of (
, questions involving ‘uniqueness implies uniqueness’, ‘uniqueness implies existence’ and ‘optimal length subintervals of (