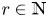Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vasilyeva, Elena
Krupnov, Yuri
Zheltenkov, A.
and
Mottaeva, A.
2020.
Development of the methodological approach to the comprehensive assessment of the innovative project effectiveness.
E3S Web of Conferences,
Vol. 164,
Issue. ,
p.
10037.
HUNTER, ZACH
and
POHOATA, COSMIN
2025.
On off-diagonal Ramsey numbers for vector spaces over
$\mathbb{F}_{2}$
.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 179,
Issue. 2,
p.
503.