Article contents
Asymptotic Formulæ for the Number of Partitions of a Multi-Partite Number
Published online by Cambridge University Press: 20 January 2009
Extract
A multi-partite number of orders j is a j dimensional vector, the components of which are non-negative rational integers. A partition of (n1, n2, …, nj) is a solution of the vector equation
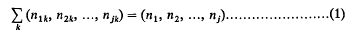
in multi-partite numbers other than (0, 0, …, 0). Two partitions, which differ only in the order of the multi-partite numbers on the left-hand side of (1), are regarded as identical. We denote by P1(n1, …, nj) the number of different partitions of (n1 …, nj) and by p2(n1, …, nj) the number of those partitions in which no part has a zero component. Also, we write P3(n1, …, nj) for the number of partitions of (n1; …, nj) into different parts and p4(n1, …, nj) for the number of partitions into different parts none of which has a zero component.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1960
References
REFERENCES
- 2
- Cited by

