Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lee, S. L.
Tan, Roger C. E.
and
Tang, W. S.
1991.
L 2-approximation by the translates of a function and related attenuation factors.
Numerische Mathematik,
Vol. 60,
Issue. 1,
p.
549.
Micula, Gheorghe
and
Micula, Sanda
1999.
Handbook of Splines.
p.
383.
Forster, Brigitte
Massopust, Peter
and
Übelacker, Thomas
2012.
Periodic Splines of Complex Order.
Numerical Functional Analysis and Optimization,
Vol. 33,
Issue. 7-9,
p.
989.

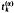 whose range is the
whose range is the 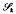 spanned by the translates of a single function. Examples of
spanned by the translates of a single function. Examples of 