Published online by Cambridge University Press: 19 November 2021
It is known that a polynomial local diffeomorphism $(f,\, g): {\mathbb {R}}^{2} \to {\mathbb {R}}^{2}$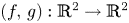 is a global diffeomorphism provided the higher homogeneous terms of $f f_x+g g_x$
is a global diffeomorphism provided the higher homogeneous terms of $f f_x+g g_x$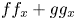 and $f f_y+g g_y$
and $f f_y+g g_y$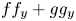 do not have real linear factors in common. Here, we give a weight-homogeneous framework of this result. Our approach uses qualitative theory of differential equations. In our reasoning, we obtain a result on polynomial Hamiltonian vector fields in the plane, generalization of a known fact.
do not have real linear factors in common. Here, we give a weight-homogeneous framework of this result. Our approach uses qualitative theory of differential equations. In our reasoning, we obtain a result on polynomial Hamiltonian vector fields in the plane, generalization of a known fact.