No CrossRef data available.
Article contents
Rigidity of Ext and Tor via flat–cotorsion theory
Published online by Cambridge University Press: 03 November 2023
Abstract
Let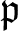 
$\mathfrak{p}$ be a prime ideal in a commutative noetherian ring R and denote by 
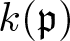$k(\mathfrak{p})$ the residue field of the local ring 
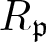$R_\mathfrak{p}$. We prove that if an R-module M satisfies 
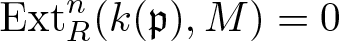$\operatorname{Ext}_R^{n}(k(\mathfrak{p}),M)=0$ for some 
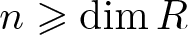$n\geqslant\dim R$, then 
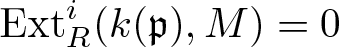$\operatorname{Ext}_R^i(k(\mathfrak{p}),M)=0$ holds for all 
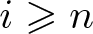$i \geqslant n$. This improves a result of Christensen, Iyengar and Marley by lowering the bound on n. We also improve existing results on Tor-rigidity. This progress is driven by the existence of minimal semi-flat-cotorsion replacements in the derived category as recently proved by Nakamura and Thompson.
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 4 , November 2023 , pp. 1142 - 1153
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
References
Alonso Tarrío, L., Jeremías López, A. and Lipman, J., Local homology and cohomology on schemes, Ann. Sci. Ec. Norm. Super. (4) 30(1) (1997), 1–39.CrossRefGoogle Scholar
Avramov, L. L. and Foxby, H.-B., Homological dimensions of unbounded complexes, J. Pure Appl. Algebra 71(2–3) (1991), 129–155.CrossRefGoogle Scholar
Bass, H., Injective dimension in Noetherian rings, Trans. Amer. Math. Soc. 102 (1962), 18–29.CrossRefGoogle Scholar
Benson, D. J., Iyengar, S. B. and Krause, H., Colocalizing subcategories and cosupport, J. Reine Angew. Math. 673 (2012), 161–207.Google Scholar
Christensen, L. W. and Holm, H., The direct limit closure of perfect complexes, J. Pure Appl. Algebra 219(3) (2015), 449–463.CrossRefGoogle Scholar
Christensen, L. W. and Iyengar, S. B., Tests for injectivity of modules over commutative rings, Collect. Math. 68(2) (2017), 243–250.CrossRefGoogle Scholar
Christensen, L. W., Iyengar, S. B. and Marley, T., Rigidity of Ext and Tor with coefficients in residue fields of a commutative Noetherian ring, Proc. Edinb. Math. Soc. (2) 62(2) (2019), 305–321.CrossRefGoogle Scholar
Christensen, L. W. and Thompson, P., Pure-minimal chain complexes, Rend. Semin. Mat. Univ. Padova 142 (2019), 41–67.CrossRefGoogle Scholar
Foxby, H.-B. and Iyengar, S., Depth and amplitude for unbounded complexes, Commutative algebra (Grenoble/Lyon, 2001) (Providence, RI). Contemp. Math. 331, Amer. Math. Soc., 2003, 119–137.CrossRefGoogle Scholar
Gillespie, J., The flat model structure on 
$\rm Ch(R)$, Trans. Amer. Math. Soc. 356(8) (2004), 3369–3390.CrossRefGoogle Scholar
$\rm Ch(R)$, Trans. Amer. Math. Soc. 356(8) (2004), 3369–3390.CrossRefGoogle ScholarIacob, A. and Iyengar, S. B., Homological dimensions and regular rings, J. Algebra 322(10) (2009), 3451–3458.CrossRefGoogle Scholar
Nakamura, T. and Thompson, P., Minimal semi-flat-cotorsion replacements and cosupport, J. Algebra 562 (2020), 587–620.CrossRefGoogle Scholar
Porta, M., Shaul, L. and Yekutieli, A., On the homology of completion and torsion, Algebr. Represent. Theory 17(1) (2014), 31–67.CrossRefGoogle Scholar
Schenzel, P. and Simon, A.-M., Completion, Čech and local homology and cohomology. Springer Monographs in Mathematics (Springer, Cham, 2018), Interactions between them.CrossRefGoogle Scholar
Thompson, P., Minimal complexes of cotorsion flat modules, Math. Scand. 124(1) (2019), 15–33.CrossRefGoogle Scholar