Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-26T03:18:11.347Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Dales–Żelazko conjecture for Beurling algebras on discrete groups

Part of: Special aspects of infinite or finite groups Structure and classification of infinite or finite groups Topological algebras, normed rings and algebras, Banach algebras Abstract harmonic analysis

Published online by Cambridge University Press:  03 July 2023

Jared T. White
Jared T. White*
Affiliation:
School of Mathematics and Statistics, The Open University, Milton Keynes, United Kingdom (jared.white@open.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a group that is either virtually soluble or virtually free, and let ω be a weight on G. We prove that if G is infinite, then there is some maximal left ideal of finite codimension in the Beurling algebra 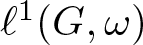$\ell^1(G, \omega)$, which fails to be (algebraically) finitely generated. This implies that a conjecture of Dales and Żelazko holds for these Banach algebras. We then go on to give examples of weighted groups for which this property fails in a strong way. For instance, we describe a Beurling algebra on an infinite group in which every closed left ideal of finite codimension is finitely generated and which has many such ideals in the sense of being residually finite dimensional. These examples seem to be hard cases for proving Dales and Żelazko’s conjecture.

Keywords

Banach algebravirtually free groupvirtually soluble groupmaximal left idealfinitely generatedweightBeurling algebra

MSC classification

Primary: 43A20: $L^1$-algebras on groups, semigroups, etc. 46H10: Ideals and subalgebras
Secondary: 20E05: Free nonabelian groups 20E08: Groups acting on trees 20F16: Solvable groups, supersolvable groups
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 3 , August 2023 , pp. 613 - 624
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Albért, M., Representing graphs by the non-commuting relation, Publ. Math. Debrecen 69(3) (2006), 261–269.CrossRefGoogle Scholar
Bartholdi, L., Grigorchuk, R. and Sunik, Z., Branch groups, in Handbook of Algebra, Volume 3, (North-Holland, Amsterdam, 2003).Google Scholar
Blecher, D. and Kania, T., Finite generation in C*-algebras and Hilbert C*-modules, Studia Math. 224 (2014), 143–151.CrossRefGoogle Scholar
Cabrera García, M., Dales, H. G. and Rodríguez Palacios, A., Maximal left ideals in Banach algebras, Bull. London Math. Soc. 52 (2020), 1–15.CrossRefGoogle Scholar
Dales, H. G. and Żelazko, W., Generators of maximal left ideals in Banach algebras, Studia Math. 212 (2012), 173–193.CrossRefGoogle Scholar
Dales, H. G., Kania, T., Kochanek, T., Koszmider, P. and Laustsen, N. J., Maximal left ideals in the Banach algebra of operators on a Banach space, Studia Math. 218 (2013), 245–286.CrossRefGoogle Scholar
Ferreira, A. V. and Tomassini, G., Finiteness properties of topological algebras, Ann. Sc. Norm. Super. Pisa Cl. Sci. 5 (1978), 471–488.Google Scholar
Malcev, A.I., On isomorphic matrix representations of infinite groups of matrices (Russian), Mat. Sb. 8 (1940), 405–422; Amer. Math. Soc. Transl. 45 (1965), 1–18.Google Scholar
Reiter, H. and Stegeman, J. D., Classical Harmonic Analysis and Locally Compact Groups, London Mathematical Society Monographs, Volume 22 (Oxford: Clarendon Press, 2000).Google Scholar
White, J. T., Finitely-generated left ideals in Banach algebras on groups and semigroups, Studia Math. 239 (2017), 67–99.CrossRefGoogle Scholar
White, J. T., Banach algebras on groups and semigroups, PhD Thesis, University of Lancaster, 2018.Google Scholar