Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-25T11:46:24.009Z Has data issue: false hasContentIssue false
  • English
  • Français

The Fueter-Sce mapping and the Clifford–Appell polynomials

Part of: Generalized function theory Spaces and algebras of analytic functions

Published online by Cambridge University Press:  28 June 2023

Antonino De Martino ,
Kamal Diki  and
Ali Guzmán Adán
Antonino De Martino
Affiliation:
Schmid College of Science and Technology, Chapman University, Orange, CA, USA (ademartino@chapman.edu; ademartino@chapman.edu)
Kamal Diki
Affiliation:
Schmid College of Science and Technology, Chapman University, Orange, CA, USA (ademartino@chapman.edu; ademartino@chapman.edu)
Ali Guzmán Adán
Affiliation:
Clifford Research Group, Department of Mathematical Analysis, Ghent University, Ghent, Belgium (aliguzmanadan@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The Fueter-Sce theorem provides a procedure to obtain axially monogenic functions, which are in the kernel of generalized Cauchy–Riemann operator in 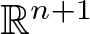${\mathbb{R}}^{n+1}$. This result is obtained by using two operators. The first one is the slice operator, which extends holomorphic functions of one complex variable to slice monogenic functions in 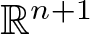$ \mathbb{R}^{n+1}$. The second one is a suitable power of the Laplace operator in n + 1 variables. Another way to get axially monogenic functions is the generalized Cauchy–Kovalevskaya (CK) extension. This characterizes axial monogenic functions by their restriction to the real line. In this paper, using the connection between the Fueter-Sce map and the generalized CK-extension, we explicitly compute the actions 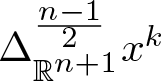$\Delta_{\mathbb{R}^{n+1}}^{\frac{n-1}{2}} x^k$, where 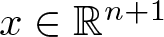$x \in \mathbb{R}^{n+1}$. The expressions obtained is related to a well-known class of Clifford–Appell polynomials. These are the building blocks to write a Taylor series for axially monogenic functions. By using the connections between the Fueter-Sce map and the generalized CK extension, we characterize the range and the kernel of the Fueter-Sce map. Furthermore, we focus on studying the Clifford–Appell–Fock space and the Clifford–Appell–Hardy space. Finally, using the polyanalytic Fueter-Sce theorems, we obtain a new family of polyanalytic monogenic polynomials, which extends to higher dimensions the Clifford–Appell polynomials.

Keywords

Fueter-Sce mapping theoremgeneralized CK extensionClifford–Appell polynomialsreproducing kernelsFock spaceHardy space

MSC classification

Primary: 30G35: Functions of hypercomplex variables and generalized variables 30H20: Bergman spaces, Fock spaces
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 3 , August 2023 , pp. 642 - 688
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alpay, D., Colombo, F. and Sabadini, I., Schur functions and their realizations in the slice hyperholomorphic setting, Integral Equations Operator Theory 72(2) (2012), 253–289.CrossRefGoogle Scholar
Alpay, D., Colombo, F. and Sabadini, I., Slice hyperholomorphic Schur analysis, in Operator Theory: Advances and Applications, Volume 256, , (Birkhäuser/Springer, Cham, 2016).Google Scholar
Alpay, D., Colombo, F. and Sabadini, I., The Fock Space as a De Branges–Rovnyak Space, Integral Equations Operator Theory 91 (2019), .CrossRefGoogle Scholar
Alpay, D., Colombo, F., Diki, K. and Sabadini, I., Poly slice monogenic functions, Cauchy formulas and the PS-functional calculus, J. Operator Theory 88(2) (2020), 309–364.Google Scholar
Alpay, D., Colombo, F., Diki, K. and Sabadini, I., On a polyanalytic approach to noncommutative de Branges–Rovnyak spaces and Schur analysis, Integr. Equ. Oper. Theory 93 (2021), .CrossRefGoogle Scholar
Alpay, D., Colombo, F., Sabadini, I. and Salomon, G., The Fock space in the slice hyperholomorphic Setting, Hypercomplex Analysis: New Perspectives and Applications, , (Trends Math., 2014).Google Scholar
Alpay, D., Diki, K. and Sabadini, I., On the global operator and Fueter mapping theorem for slice polyanalytic functions, J. Math. Anal. Appl. 19(6) (2021), 941–964.Google Scholar
Alpay, D., Diki, K. and Sabadini, I., Correction to: On slice polyanalytic functions of a quaternionic variable, Results Math. 76 (2021), .CrossRefGoogle Scholar
Alpay, D., Diki, K. and Sabadini, I., Fock and Hardy spaces: Clifford Appell case, Math. Nachr. 295(5) (2022), 834–860.CrossRefGoogle Scholar
Appell, P., Sur une classe de polynomes, Ann. Sci. de l’E.N.S 2eme serie, Tome 9 (1880), 119–144.Google Scholar
Balk, M., Polyanalytic functions (Akademie-Verlag, Berlin, 1991).Google Scholar
Bao, Q. T., Probabilistic approach to Appell polynomials, Expo. Math. 33 (2015), 269–294.Google Scholar
Brackx, F., On (k)-monogenic functions of a quaternion variable, in Function Theoretic Methods in Differential Equations, Volume 8, , Res. Notes in Math. (Pitman, London, 1976).Google Scholar
Brackx, F. and Delanghe, R., Hypercomplex function theory and Hilbert modules with reproducing kernel, Proceedings of the London Mathematical Society, 37(3) (1978), 545–576.Google Scholar
Brackx, F., Delanghe, R. and Sommen, F., Clifford analysis, Research Notes in Mathematics, 76, Pitman (Advanced Publishing Program), Boston, MA (1982), .Google Scholar
Cação, I., Falcão, M. I. and Malonek, H., Hypercomplex polynomials, Vietoris’ rational numbers and a related integer numbers sequence, Complex Anal. Oper. Theory 11 (2017), 1059–1076.CrossRefGoogle Scholar
Colombo, F., De Martino, A., Pinton, S. and Sabadini, I., Axially harmonic functions and the harmonic functional calculus on the S-spectrum, J. Geom. Anal. 33(1) (2023), .CrossRefGoogle Scholar
Colombo, F., Gonzalez-Cervantes, J. O. and Sabadini, I., On bislice regular functions and isomorphisms of Bergmann spaces, Complex Var. Elliptic Equ. 57(7–8) (2012), 825–839.CrossRefGoogle Scholar
Colombo, F., Gonzalez-Cervantes, J. O. and Sabadini, I., A nonconstant coefficients differential operator associated to slice monogenic functions, Trans. Amer. Math. Soc. 365 (2013), 303–318.CrossRefGoogle Scholar
Colombo, F., Krausshar, R. S. and Sabadini, I., Symmetries of slice monogenic functions, J. Noncommut. Geom. 14 (2020), 1075–1106.CrossRefGoogle Scholar
Colombo, F., Sabadini, I. and Sommen, F., The Fueter mapping theorem in integral form and the F-functional calculus, Math. Methods Appl. Sci. 33 (2010), 2050–2066.CrossRefGoogle Scholar
Colombo, F., Sabadini, I. and Struppa, D. C., Noncommutative functional calculus. Theory and applications of slice hyperholomorphic functions, in Progress in Mathematics, Volume 289, , (Birkhäuser/Springer Basel AG, Basel, 2011).Google Scholar
Colombo, F., Sabadini, I. and Struppa, D. C., Entire Slice Regular Functions, in SpringerBriefs in Mathematics., , (Springer, Cham, 2016).Google Scholar
Colombo, F., Sabadini, I. and Struppa, D. C., Michele Sce’s Works in Hypercomplex Analysis, in A Translation with Commentaries, Volume vi, , (Birkhäuser, Cham, 2020).Google Scholar
De Martino, A. and Diki, K., Generalized Appell polynomials and Fueter-Bargmann transforms in the quaternionic setting. Anal. Appl. 21(3) (2023), 677–718.CrossRefGoogle Scholar
De Martino, A. and Diki, K., On the inversion of the polyanalytic Fueter maps, in preparation.Google Scholar
De Martino, A., Diki, K. and Guzmán Adán, A., On the connection between the Fueter mapping theorem and the generalized CK-extension, Results Math. 78(2) (2023), .CrossRefGoogle Scholar
De Schepper, N. and Sommen, F., Cauchy-Kowalevski extensions and monogenic plane waves in Clifford analysis, Adv. Appl. Clifford Algebra 22(3) (2012), 625–647.CrossRefGoogle Scholar
De Schepper, N. and Sommen, F., Cauchy-Kowalevski extensions and monogenic plane waves using spherical monogenics, Bull. Braz. Math Soc.(N.S) 44(2) (2013), 321–350.CrossRefGoogle Scholar
Delanghe, R., Sommen, F. and Soucek, V., Clifford algebra and spinor-valued functions, in A Function Theory for the Dirac Operator, Mathematics and its Applications, Volume 53 (Kluwer Academic Publishers Group, Dordrecht, 1992).Google Scholar
Diki, K., Krausshar, R. S. and Sabadini, I., On the Bargmann-Fock-Fueter and Bergman-Fueter integral transforms, J. Math. Phys. 60 (2019), .CrossRefGoogle Scholar
Eelbode, D., The biaxial Fueter theorem, Israel J. Math. 201 (2014), 233–245.CrossRefGoogle Scholar
Eelbode, D., Hohloch, S. and Muarem, G., The symplectic Fueter-Sce theorem, Adv. Appl. Clifford Algebr. 30(4) (2020), .CrossRefGoogle Scholar
Falcão, M.I. and Malonek, H., Special monogenic polynomials – Properties and applications, International Conference on Numerical Analysis and Applied Mathematics, 936, AIP-Proceedings, (2007), .Google Scholar
Fock, V., Verallgemeinerung und Lösung der Diracschen statistischen Gleichung, Z. Phys. 49 (1928), 339–357.CrossRefGoogle Scholar
Gürlebeck, K., Habetha, K. and Sprößig, W., Holomorphic Functions in the Plane and n-Dimensional Space (Birkhäuser, Basel, 2008).Google Scholar
Ghiloni, R. and Perotti, A., Global differential equations for slice regular functions, Math. Nachr. 287 (2014), 561–573.CrossRefGoogle Scholar
Guzmàn Adàn, A., Generalized Cauchy-Kovalevskaya extension and plane wave decomposition in superspace, Ann. Mat. Pura Appl. 4 (2021), .Google Scholar
Kou, K. I., Qian, T. and Sommen, F., Generalizations of Fueter’s theorem, Methods Appl. Anal. 9 (2002), 273–290.CrossRefGoogle Scholar
Malonek, H. R., Laguerre derivative and monogenic Laguerre polynomials: An operational approach, Math. Comput. Model. 53 (2011), 1084–1094.Google Scholar
Pena-Pena, D., Shifted Appell sequences in clifford analysis, Results Math. 63 (2013), 1145–1157.CrossRefGoogle Scholar
Pena-Pena, D., Qian, T. and Sommen, F., An alternative proof of Fueter’s theorem, Complex Var. Elliptic Equ. 51 (2006), 913–922.CrossRefGoogle Scholar
Pena-Pena, D., Sabadini, I. and Sommen, F., Fueter’s theorem for monogenic functions in biaxial symmetric domains, Results Math. 72 (2017), 1747–1758.CrossRefGoogle Scholar
Qian, T., Generalization of Fueters result to $ \mathbb{R}^{n+1}$, Rend. Mat. Acc. Lincei 9 (1997), 111–117.Google Scholar
Ren, G. and Wang, X., Growth and distortion theorems for slice monogenic functions, Pacific J. Math. 290 (2017), 169–198.CrossRefGoogle Scholar
Salminen, P., Optimal stopping, Appell polynomials, and Wiener–Hopf factorization, Stochastics 83 (2011), 611–622.CrossRefGoogle Scholar
Sce, M., Osservazioni sulle serie di potenze nei moduli quadratici, Atti Accad. Naz. Lincei. Rend. CI. Sci. Fis. Mat. Natur. 23 (1957), 220–225.Google Scholar
Sommen, F., Special functions in Clifford analysis and axial symmetry, J. Math. Anal. Appl. 130(1) (1988), 110–133.CrossRefGoogle Scholar
Sommen, F., On a generalization of Fueter’s theorem, Z. Anal. Anwend. 19 (2000), 899–902.CrossRefGoogle Scholar