No CrossRef data available.
Article contents
Examples of multiparameter CCR flows with non-trivial index
Part of:
Selfadjoint operator algebras
Published online by Cambridge University Press: 27 September 2022
Abstract
In this paper, we construct uncountably many examples of multiparameter CCR flows, which are not pullbacks of $1$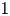 -parameter CCR flows, with any given index. Moreover, the constructed CCR flows are type I in the sense that the associated product system is the smallest subsystem containing its units.
-parameter CCR flows, with any given index. Moreover, the constructed CCR flows are type I in the sense that the associated product system is the smallest subsystem containing its units.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 3 , August 2022 , pp. 799 - 832
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society
References
Arjunan, A., Srinivasan, R. and Sundar, S., $E$ -semigroups over closed convex cones, J. Operator Theory 84 (2) (2020), 289–322.CrossRefGoogle Scholar
-semigroups over closed convex cones, J. Operator Theory 84 (2) (2020), 289–322.CrossRefGoogle Scholar
Arjunan, A. and Sundar, S., CCR flows associated to closed convex cones, Münster J. Math. 13(2020), 115–143.Google Scholar
Arveson, W., Continuous analogues of Fock space, Mem. Amer. Math. Soc. 80 (409) (1989).Google Scholar
Arveson, W., Noncommutative dynamics and E-semigroups, Springer Monographs in Mathematics (Springer-Verlag, New York, 2003).CrossRefGoogle Scholar
Borel, A., Semisimple groups and Riemannian symmetric spaces, Texts and Readings in Mathematics, Volume 16 (Hindustan Book Agency, New Delhi, 1998).CrossRefGoogle Scholar
Faraut, J. and Korányi, A., Analysis on symmetric cones (Oxford Mathematical Monographs, 1994).Google Scholar
Hilgert, J., Hofmann, K. H. and Lawson, J. D., Lie groups, convex cones, and semigroups, Oxford Mathematical Monographs, (Oxford Science Publications, 1989).Google Scholar
Hilgert, J. and Neeb, K.-H., Lie semigroups and their applications, Lecture Notes in Mathematics, Volume 1552, Springer-Verlag, Berlin, 1993.CrossRefGoogle Scholar
Hilgert, J. and Neeb, K.-H., Wiener-Hopf operators on ordered homogeneous spaces. I, J. Funct. Anal. 132(1995), 86–118.CrossRefGoogle Scholar
Izumi, M. and Srinivasan, R., Generalized CCR flows, Comm. Math. Phys. 281 (2) (2008), 529–571.CrossRefGoogle Scholar
Izumi, M. and Srinivasan, R., Toeplitz CAR flows and type I factorizations, Kyoto J. Math. 50 (1) (2010), 1–32.CrossRefGoogle Scholar
Laca, M. and Raeburn, I., Extending multipliers from semigroups, Proc. Amer. Math. Soc. 123 (2) (1995), 355–362.CrossRefGoogle Scholar
Liebscher, V., Random sets and invariants for (type II) continuous tensor product systems of Hilbert spaces, Mem. Amer. Math. Soc. 199 (930) (2009).Google Scholar
Murugan, S.P. and Sundar, S., On the existence of $E_0$ -semigroups – the multiparameter case, Infin. Dimens. Anal. Quantum Probab. Relat. Top. 21 (2) (2018), 185007–185027.CrossRefGoogle Scholar
-semigroups – the multiparameter case, Infin. Dimens. Anal. Quantum Probab. Relat. Top. 21 (2) (2018), 185007–185027.CrossRefGoogle Scholar
Powers, R. T., A nonspatial continuous semigroup of $*$ -endomorphisms of $B(H)$
-endomorphisms of $B(H)$ , Publ. Res. Inst. Math. Sci. 23 (6) (1987), 1053–1069.CrossRefGoogle Scholar
, Publ. Res. Inst. Math. Sci. 23 (6) (1987), 1053–1069.CrossRefGoogle Scholar
Powers, R. T., New examples of continuous spatial semigroups of $*$ -endomorphisms of $B(H)$
-endomorphisms of $B(H)$ , Internat. J. Math. 10 (2) (1999), 215–288.CrossRefGoogle Scholar
, Internat. J. Math. 10 (2) (1999), 215–288.CrossRefGoogle Scholar
Shalit, O. and Skeide, M. CP-semigroups and dilations, SubProduct systems and SuperProduct systems: The Multiparameter Case and Beyond, e-print https://arxiv/math.OA:2003.05166.Google Scholar
Shalit, O. M., $E_0$ -dilation of strongly continuous $CP_0$
-dilation of strongly continuous $CP_0$ -semigroups, J. Funct. Anal. 255 (1) (2008), 46–89.CrossRefGoogle Scholar
-semigroups, J. Funct. Anal. 255 (1) (2008), 46–89.CrossRefGoogle Scholar
Shalit, O. M., What type of dynamics arise in $E_0$ -dilations of commuting quantum Markov semigroups?, Infin. Dimens. Anal. Quantum. Probab. Relat. Top. 11 (3) (2008), 393–403.CrossRefGoogle Scholar
-dilations of commuting quantum Markov semigroups?, Infin. Dimens. Anal. Quantum. Probab. Relat. Top. 11 (3) (2008), 393–403.CrossRefGoogle Scholar
Shalit, O. M., $E$ -dilation of strongly commuting $CP$
-dilation of strongly commuting $CP$ -semigroups (the nonunital case), Houston J. Math. 37 (1) (2011), 203–232.Google Scholar
-semigroups (the nonunital case), Houston J. Math. 37 (1) (2011), 203–232.Google Scholar
Srinivasan, R., CCR and CAR flows over convex cones, e-print https://arxiv/math.OA:1908.00188v1.Google Scholar
Sundar, S., $C^{*}$ -algebras associated to topological ore semigroups, Münster J. Math. 9 (1) (2016), 155–185.Google Scholar
-algebras associated to topological ore semigroups, Münster J. Math. 9 (1) (2016), 155–185.Google Scholar
Sundar, S., Arveson's characterisation of CCR flows: the multiparameter case, J. Funct. Anal. 280 (1) (2021),108802–108846.CrossRefGoogle Scholar
Tsirelson, B., From random sets to continuous tensor products: answers to three questions of W. Arveson, e-print arxiv/math.FA:0001070.Google Scholar
Tsirelson, B., Non-isomorphic product systems. Advances in quantum dynamics,Contemp. Math., Amer. Math. Soc., Providence, RI 335 (2003) 273–328.Google Scholar
Williams, D. P., Crossed products of $C^{*}$ -algebras, Mathematical Surveys and Monographs, Volume 134 (Amer. Math. Soc., Providence, RI, 2007).CrossRefGoogle Scholar
-algebras, Mathematical Surveys and Monographs, Volume 134 (Amer. Math. Soc., Providence, RI, 2007).CrossRefGoogle Scholar


