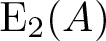Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mirzaii, Behrooz
and
Pérez, Elvis Torres
2025.
On the connections between the low dimensional homology groups of SL
2
and PSL
2
.
Communications in Algebra,
Vol. 53,
Issue. 11,
p.
4939.
Mirzaii, Behrooz
Ramos, Bruno R.
and
Verissimo, Thiago
2026.
Abelianization of SL2 over Dedekind domains of arithmetic type.
Journal of Algebra,
Vol. 688,
Issue. ,
p.
1.