Article contents
DES AND RES PROCESSES AND THEIR EXPLICIT SOLUTIONS
Published online by Cambridge University Press: 22 December 2014
Abstract
This paper defines and studies the down entrance state (DES) and the restart entrance state (RES) classes of quasi-skip free (QSF) processes specified in terms of the nonzero structure of the elements of their transition rate matrix Q. A QSF process is a Markov chain with states that can be specified by tuples of the form (m, i), where 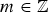 $m \in {\open Z}$ represents the “current” level of the state and
$m \in {\open Z}$ represents the “current” level of the state and 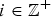 $i \in {\open Z}^{+}$ the current phase of the state, and its transition probability matrix Q does not permit one-step transitions to states that are two or more levels away from the current state in one direction of the level variable m. A QSF process is a DES process if and only if one step “down” transitions from a level m can only reach a single state in level m − 1, for all m. A QSF process is a RES process if and only if one step “up” transitions from a level m can only reach a single set of states in the highest level M2, largest of all m.
$i \in {\open Z}^{+}$ the current phase of the state, and its transition probability matrix Q does not permit one-step transitions to states that are two or more levels away from the current state in one direction of the level variable m. A QSF process is a DES process if and only if one step “down” transitions from a level m can only reach a single state in level m − 1, for all m. A QSF process is a RES process if and only if one step “up” transitions from a level m can only reach a single set of states in the highest level M2, largest of all m.
We derive explicit solutions and simple truncation bounds for the steady-state probabilities of both DES and RES processes, when in addition Q insures ergodicity. DES and RES processes have applications in many areas of applied probability comprising computer science, queueing theory, inventory theory, reliability, and the theory of branching processes. To motivate their applicability we present explicit solutions for the well-known open problem of the M/Er/n queue with batch arrivals, an inventory model, and a reliability model.
Information
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 29 , Issue 2 , April 2015 , pp. 191 - 217
- Copyright
- Copyright © Cambridge University Press 2014
References
- 10
- Cited by

