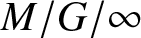1. Introduction
For applications in computer science and telecommunications, it is of interest to study the time it takes for a processor to complete a task of random size when the service can be interrupted or slowed down by the occurrence of random failures or higher priority task arrivals to processor sharing systems. This line of research on interrupted service times that leads to our study started in the sixties with the work of Gaver [Reference Gaver18] that investigates the completion time distribution of a task experiencing complete service breakdowns during which times the server stops processing the task. Either the interruption can be postponed until the current task is completed or the current task is preempted whenever an interruption occurs and then the server decides on a preemption scheme/discipline. The preemption scheme determines the course of action for the server when a task has been interrupted. Gaver [Reference Gaver18] is the first to consider postponable interruptions in addition to the following types of preemption strategies: (1) Preempt-RESUME, once the interruption is cleared the server continues with the unfinished task from where it left. (2) Preempt-REPLACE (repeat different), the server discards the unfinished task to revisit later and selects a different task, assuming that such similar tasks are always available. (3) Preempt-RESTART (repeat identical), the server starts the unfinished task from the beginning. The author derives the Laplace–Stieltjes transform (Laplace–Stieltjes transform) of the completion time distribution under each interruption/recovery type by counting the number of interruptions until task completion. In [Reference Gaver18], the service times are generally distributed while the interruptions arrive as a Poisson process with generally distributed down times.
Such service completion systems have found many opportunities in queuing applications. Researchers investigate the Laplace–Stieltjes transform of the stationary number of customers in the system of an ![]() $M/M/1$ queue under server breakdowns [Reference Avi-Itzhak and Naor4, Reference White and Christie38], and of an
$M/M/1$ queue under server breakdowns [Reference Avi-Itzhak and Naor4, Reference White and Christie38], and of an ![]() $M/M/c$ queue under independent server breakdowns [Reference Mitrany and Avi-Itzhak27]. Coffman et al. [Reference Coffman, Muntz and Trotter11] study a processor-sharing
$M/M/c$ queue under independent server breakdowns [Reference Mitrany and Avi-Itzhak27]. Coffman et al. [Reference Coffman, Muntz and Trotter11] study a processor-sharing ![]() $M/M/1$ queue. The authors obtain the Laplace–Stieltjes transform and the first two moments of the stationary waiting time distribution. Others extend this research to the partial failure case [Reference Eisen and Tainiter13, Reference Purdue33, Reference Yechiali and Naor39]. Such service systems are called Markovian service process (MSP). Nicola [Reference Nicola30] considers a mixture of interruption types affecting a single server as Poisson arrivals. He obtains the Laplace–Stieltjes transform of task completion time distribution under various types of interruptions. Kulkarni et al. [Reference Kulkarni, Nicola and Trivedi25] investigate a server affected by a Markov modulated environment in which the service rate in each environmental state is different, that is, the service deteriorates. The authors derive the Laplace–Stieltjes transform of the completion time distribution under each type of recovery schemes using renewal arguments. Furthermore the authors assume that associated to each environmental state a recovery scheme is fixed as either preempt-resume or preempt-restart discipline. They generalize their results to the semi-Markovian environment in [Reference Kulkarni, Nicola and Trivedi24]. Furthermore, the authors apply their results for preempt-resume service discipline to a processor sharing
$M/M/1$ queue. The authors obtain the Laplace–Stieltjes transform and the first two moments of the stationary waiting time distribution. Others extend this research to the partial failure case [Reference Eisen and Tainiter13, Reference Purdue33, Reference Yechiali and Naor39]. Such service systems are called Markovian service process (MSP). Nicola [Reference Nicola30] considers a mixture of interruption types affecting a single server as Poisson arrivals. He obtains the Laplace–Stieltjes transform of task completion time distribution under various types of interruptions. Kulkarni et al. [Reference Kulkarni, Nicola and Trivedi25] investigate a server affected by a Markov modulated environment in which the service rate in each environmental state is different, that is, the service deteriorates. The authors derive the Laplace–Stieltjes transform of the completion time distribution under each type of recovery schemes using renewal arguments. Furthermore the authors assume that associated to each environmental state a recovery scheme is fixed as either preempt-resume or preempt-restart discipline. They generalize their results to the semi-Markovian environment in [Reference Kulkarni, Nicola and Trivedi24]. Furthermore, the authors apply their results for preempt-resume service discipline to a processor sharing ![]() $M/M/1$ queue. Nicola et al. [Reference Nicola, Kulkarni and Trivedi31] analyze a single server queue with Markov modulated service process, and demonstrate that the queue has a block M/G/
$M/M/1$ queue. Nicola et al. [Reference Nicola, Kulkarni and Trivedi31] analyze a single server queue with Markov modulated service process, and demonstrate that the queue has a block M/G/![]() $\infty$ structure and provide a procedure to evaluate the moment generating function for the stationary distribution of the number of jobs in the system. Again under preempt-resume service discipline, Boxma and Kurkova [Reference Boxma and Kurkova10] consider an
$\infty$ structure and provide a procedure to evaluate the moment generating function for the stationary distribution of the number of jobs in the system. Again under preempt-resume service discipline, Boxma and Kurkova [Reference Boxma and Kurkova10] consider an ![]() $M/M/1$ queue served under alternating speed and generally distributed low-speed times, and investigate the tail behavior of the workload distribution. Baykal-Gürsoy and Xiao [Reference Baykal-Gürsoy and Xiao7] study an infinite server queue with two-state Markovian arrival and service processes. Using transform methods, they show that the stationary distribution of the number of jobs in the system is a mixture of two randomized Poisson distributions. Thus show the validity of the stochastic decomposition property. However, this property is not valid for
$M/M/1$ queue served under alternating speed and generally distributed low-speed times, and investigate the tail behavior of the workload distribution. Baykal-Gürsoy and Xiao [Reference Baykal-Gürsoy and Xiao7] study an infinite server queue with two-state Markovian arrival and service processes. Using transform methods, they show that the stationary distribution of the number of jobs in the system is a mixture of two randomized Poisson distributions. Thus show the validity of the stochastic decomposition property. However, this property is not valid for ![]() $M/M/c$ queues under two-state service system [Reference Baykal-Gürsoy, Xiao and Ozbay8, Reference Neuts28, Reference Neuts29]. Following Neuts [Reference Neuts28], others [Reference Katehakis, Smit and Spieksma23, Reference O’Cinneide and Purdue32] use matrix-analytic methods to solve for the stationary distribution of multi-dimensional queues.
$M/M/c$ queues under two-state service system [Reference Baykal-Gürsoy, Xiao and Ozbay8, Reference Neuts28, Reference Neuts29]. Following Neuts [Reference Neuts28], others [Reference Katehakis, Smit and Spieksma23, Reference O’Cinneide and Purdue32] use matrix-analytic methods to solve for the stationary distribution of multi-dimensional queues.
For the complete service breakdown case, Gaver [Reference Gaver18] is the first to notice that under the restart strategy the first two moments of the task completion time may not always exist. Later Fiorini et al. [Reference Fiorini, Sheahan and Lipsky16] and Sheahan et al. [Reference Sheahan, Lipsky, Fiorini and Asmussen34] show that under the restart strategy and the same exponential up time assumption, the total time it takes to execute a task not including failures follows a power tailed distribution even when the task service time has exponential tail. Asmussen et al. [Reference Asmussen, Fiorini, Lipsky, Rolski and Sheahan2] further extend the asymptotic analysis of the restart case in Sheahan et al. [Reference Sheahan, Lipsky, Fiorini and Asmussen34] to more general up time and task time distributions. They notice that the relationship between the up time and task time distributions play an important role impacting the distribution of completion times. In [Reference Asmussen, Lipsky and Thompson3], Asmussen, Lipsky, and Thompson show that task completion time is heavy-tailed if the task time has unbounded support. Jelenković and Tan [Reference Jelenković and Tan21] independently study the same restart strategy and approach the analysis by first proving that the number of restarts is power tailed, and then using large deviation theory show that the completion times also have power law distribution irrespective of how heavy or light the distributions of task times and up times may be. Jelenković and Tan [Reference Jelenković and Tan22] extend these results to analyze further how a certain functional relationship between the tail distributions of the up time and task time distributions impacts the distributions of the number of restarts and the completion times.
In this paper, we study the completion time distribution of a task processed by a server experiencing service interruptions. The processor starts working on a task at a random time, and during the interruptions the server works at a lower service rate. Firstly, we derive the Laplace–Stieltjes transform of the completion time distributions under both replace and restart service disciplines using counting arguments. The approach that we present here yields more detailed results than Kulkarni et al. [Reference Kulkarni, Nicola and Trivedi24] and Asmussen et al. [Reference Asmussen, Lipsky and Thompson3] for our specific cases. Secondly, we show the asymptotic behavior of these distributions and prove that under the RESTART service discipline the completion time has power tail more directly than Asmussen et al. [Reference Asmussen, Lipsky and Thompson3]. Finally, we apply our results to an infinite server queue in which the servers experience Markovian partial failures. Using Little’s law, we compare the stationary system size and system time distributions of customers in a two server state M/MSP/![]() $\infty$ queue, and in a M/G/
$\infty$ queue, and in a M/G/![]() $\infty$ queue in which each server experiencing Markovian service interruptions independently of the others.
$\infty$ queue in which each server experiencing Markovian service interruptions independently of the others.
Section 2 presents the service model for both cases in detail, introducing the corresponding notation and giving the main analytical results for general and specific task-size distributions. Section 3 deals with the asymptotic classification of the resulting completion-time distributions for both the replace and restart cases. It demonstrates that for the restart case not all moments may exists. Section 4 considers the application of our results to an infinite server queue with Poisson arrivals, and service interruptions, and exhibits the insensitivity of the stationary first moments of the system size and system time random variables to system-wide or independent interruptions. Finally, in Section 5, we draw the conclusions of the study and discuss some directions to extend the research.
2. Service model
We consider an unreliable server which from time to time experiences partial failures that reduce the service speed. Upon completion of a repair the server resumes its normal operation speed. We call the periods that the server works with normal speed as up periods, and the periods that the server works with low speed as down periods. It is so that the server state follows an alternating renewal process of up and down periods.
In general, for a continuous random variable C, we denote its probability density function (pdf) ![]() $f_C(t)$, cumulative distribution function (cdf) by
$f_C(t)$, cumulative distribution function (cdf) by ![]() $F_C(t)$, tail distribution by
$F_C(t)$, tail distribution by ![]() $\overline{F_C(t)}$, and its Laplace–Stieltjes transform by
$\overline{F_C(t)}$, and its Laplace–Stieltjes transform by ![]() $L_C(s)$.
$L_C(s)$.
We denote by ![]() $F_S(t)$ the cdf for the task size, with pdf
$F_S(t)$ the cdf for the task size, with pdf ![]() $f_S(t)$, tail distribution
$f_S(t)$, tail distribution ![]() $\overline{F_S(t)}$, Laplace–Stieltjes transform
$\overline{F_S(t)}$, Laplace–Stieltjes transform ![]() $L_S(s)$, and mean task size
$L_S(s)$, and mean task size ![]() $1/\mu$, µ > 0. The task size random variable denoted by S is generally distributed. In literature, this quantity is also called as service time requirement.
$1/\mu$, µ > 0. The task size random variable denoted by S is generally distributed. In literature, this quantity is also called as service time requirement.
The up period duration random variable U is exponentially distributed, except noted otherwise, with mean ![]() $1/f$,
$1/f$, ![]() $f\geq0$. However, down period duration D is generally distributed with
$f\geq0$. However, down period duration D is generally distributed with ![]() $f_D(t)$,
$f_D(t)$, ![]() $F_D(t)$,
$F_D(t)$, ![]() $\overline{F_D(t)}$,
$\overline{F_D(t)}$, ![]() $L_D(s)$, and mean duration
$L_D(s)$, and mean duration ![]() $1/r$,
$1/r$, ![]() $r\geq0$. Notice that f and r can be interpreted as failure and repair rates of the server, respectively.
$r\geq0$. Notice that f and r can be interpreted as failure and repair rates of the server, respectively.
When technical reasons require its definition we will denote the remaining down time for a customer who arrives during down time by Y. It is clear that Y is generally distributed unless D is an exponential random variable.
Finally, without loss of generality the server’s normal service speed is considered to be 1, and when a failure happens, the service speed drops to α with ![]() $0 \lt \alpha \lt 1$. As α does not necessarily take the value of zero this kind of service interruption is called partial failure. Note that in this system, a task may be finished during an up period or a down period.
$0 \lt \alpha \lt 1$. As α does not necessarily take the value of zero this kind of service interruption is called partial failure. Note that in this system, a task may be finished during an up period or a down period.
The objective is to derive closed form expressions for the distribution of the task completion time random variable, which is denoted by T for both preempt-replace and preempt-restart service disciplines. Although, for the replace case, a general procedure to calculate the distribution of T in the frequency domain can be found in the works by Kulkarni et al. [Reference Kulkarni, Nicola and Trivedi24, Reference Kulkarni, Nicola and Trivedi25], we use a much simpler counting argument for our particular class of service systems yielding more detailed results. In fact, the same argument will also be utilized to analyze the restart service discipline.
If work on a task starts at a random instance, the completion time can be obtained by conditioning it on the instance the work starts on a task. Let us call ![]() $G^{1},$ the event in which the work starts during an up period, and
$G^{1},$ the event in which the work starts during an up period, and ![]() $G^2,$ the event in which the work starts during a down period. In particular, by renewal arguments it holds that:
$G^2,$ the event in which the work starts during a down period. In particular, by renewal arguments it holds that:
 \begin{align}
P\left\{G^1\right\}=\frac{r}{f+r}, \qquad P\left\{G^2\right\}=\frac{f}{f+r}.
\end{align}
\begin{align}
P\left\{G^1\right\}=\frac{r}{f+r}, \qquad P\left\{G^2\right\}=\frac{f}{f+r}.
\end{align}The Laplace–Stieltjes transform of the conditional completion time is calculated separately for each one of these events, and then the Laplace–Stieltjes transform of the unconditional completion time is derived. Note that, one can assume that work always starts when the server is working under normal speed, then the conditional completion time under G 1 gives the full task completion time information.
We start by studying the completion time of a task under G 1.
Consider that the work on a task starts at an up period, and denote the subsequent up and down periods as Ui and Di, respectively, for ![]() $i=1,2,3,\ldots$. The service requirement on each period is denoted as Si,
$i=1,2,3,\ldots$. The service requirement on each period is denoted as Si, ![]() $i=1,2,3,\ldots$. Figure 1 shows a sample path of how the system may evolve. Since up period durations are exponentially distributed, one can assume that the work starts at time zero, and we denote with crosses on the time-axis some possible departure times (realizations of the completion time).
$i=1,2,3,\ldots$. Figure 1 shows a sample path of how the system may evolve. Since up period durations are exponentially distributed, one can assume that the work starts at time zero, and we denote with crosses on the time-axis some possible departure times (realizations of the completion time).

Figure 1. Sample path of the service system under G 1.
Hence, the conditional completion time given that the work starts during up period, ![]() $\{T| G^1\}$, can be written as
$\{T| G^1\}$, can be written as
 \begin{equation}
\{T| G^1\}=
\begin{cases}
\sum_{i=1}^{n}\left(U_{i} + D_i\right) + S_{2n+1}, & \quad \mbox{event }A_n,\\
\sum_{i=1}^{n+1}U_i+\sum_{i=1}^n D_i+\frac{1}{\alpha}S_{2n+2}, & \quad \mbox{event }E_n,
\end{cases}
\quad
n = 0,1,2,\ldots,
\end{equation}
\begin{equation}
\{T| G^1\}=
\begin{cases}
\sum_{i=1}^{n}\left(U_{i} + D_i\right) + S_{2n+1}, & \quad \mbox{event }A_n,\\
\sum_{i=1}^{n+1}U_i+\sum_{i=1}^n D_i+\frac{1}{\alpha}S_{2n+2}, & \quad \mbox{event }E_n,
\end{cases}
\quad
n = 0,1,2,\ldots,
\end{equation}in terms of events An and En. Given that the works starts during an up period, An denotes the case that the completion time is composed of n complete up and down periods with an incomplete up period finishing the task, and event En denotes the case with n + 1 up periods and n down periods with an incomplete down period finishing the task. In general, A denotes the case that the work on a task starts and ends at the same regime, while E denotes the case that the work starts and ends at different regimes.
Similarly, the conditional completion time given that the work starts at a down period, ![]() $\{T|G^2\}$, will be:
$\{T|G^2\}$, will be:
 \begin{equation}
\{T|G^2\}=
\begin{cases}
\frac{1}{\alpha}S_1, & \quad \mbox{event }A_0, \\
Y+\sum_{i=2}^nD_i+\sum_{i=1}^{n}U_i+\frac{1}{\alpha}S_{2n+1}, & \quad \mbox{event }A_n, \quad n = 1,2,\ldots \\
Y+\sum_{i=2}^{n+1}D_i+\sum_{i=1}^nU_i+S_{2n+2}, & \quad \mbox{event }E_n, \quad n = 0,1,2,\ldots
\end{cases},
\end{equation}
\begin{equation}
\{T|G^2\}=
\begin{cases}
\frac{1}{\alpha}S_1, & \quad \mbox{event }A_0, \\
Y+\sum_{i=2}^nD_i+\sum_{i=1}^{n}U_i+\frac{1}{\alpha}S_{2n+1}, & \quad \mbox{event }A_n, \quad n = 1,2,\ldots \\
Y+\sum_{i=2}^{n+1}D_i+\sum_{i=1}^nU_i+S_{2n+2}, & \quad \mbox{event }E_n, \quad n = 0,1,2,\ldots
\end{cases},
\end{equation}with event An representing the case that the completion time is composed of one residual down time denoted by Y, and n − 1 complete down and n complete up periods with an incomplete down period finishing the task, and En representing the case that the completion time is composed of one residual down period, and n complete down and up periods with an incomplete up period finishing the task. Next, we will first analyze preempt-replace and then study preempt-restart service disciplines.
2.1. Preempt-REPLACE service discipline
In the case that the service times (task size) are generally distributed, we assume that any state change reinitiates the service for the current task with the same service requirement distribution, that is, all Sn’s for ![]() $n = 1, 2, \ldots$ are i.i.d. This last consideration corresponds to the preemption discipline called repeat different or replace, since the service requirement is resampled at each service-speed change. This is also equivalent to replacing the task with a similar one with the same task size distribution.
$n = 1, 2, \ldots$ are i.i.d. This last consideration corresponds to the preemption discipline called repeat different or replace, since the service requirement is resampled at each service-speed change. This is also equivalent to replacing the task with a similar one with the same task size distribution.
Proposition 2.1 shows the resulting completion time pdf in the frequency domain.
Proposition 2.1. Consider a two-service-speed server as described above. Then, the Laplace–Stieltjes transform of the completion time random variable T is given in Eqs. (2.4)–(2.5).
 \begin{align}
L_T(s)
& = E[e^{-sT}] \nonumber \\
& =
\frac{1}{1-V(s)}
\Biggl\{\Biggr.
\left(
L_S(s+f)
+
\frac{f}{s+f}[1-L_S(s+f)]
\left[L_S(s/\alpha)-\int_0^\infty e^{-(s/\alpha)t}F_D(t/\alpha)dF_{S}(t)\right]
\right)
\nonumber \\
& \phantom{=}\,\,\,
\cdot
\left(
\frac{r}{r+f} + \frac{f}{r+f}\left[L_Y(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_{Y}(t)\right]
\right)
\Biggl.\Biggr\}
+
\frac{f}{r+f}
\left[\vphantom{\left.-\int_0^\infty e^{-(s/\alpha) t} F_Y(t/\alpha) dF_{S}(t)\right]}L_S(s/\alpha) \right. \nonumber\\
&\quad \left.-\int_0^\infty e^{-(s/\alpha) t} F_Y(t/\alpha) dF_{S}(t)\right],
\end{align}
\begin{align}
L_T(s)
& = E[e^{-sT}] \nonumber \\
& =
\frac{1}{1-V(s)}
\Biggl\{\Biggr.
\left(
L_S(s+f)
+
\frac{f}{s+f}[1-L_S(s+f)]
\left[L_S(s/\alpha)-\int_0^\infty e^{-(s/\alpha)t}F_D(t/\alpha)dF_{S}(t)\right]
\right)
\nonumber \\
& \phantom{=}\,\,\,
\cdot
\left(
\frac{r}{r+f} + \frac{f}{r+f}\left[L_Y(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_{Y}(t)\right]
\right)
\Biggl.\Biggr\}
+
\frac{f}{r+f}
\left[\vphantom{\left.-\int_0^\infty e^{-(s/\alpha) t} F_Y(t/\alpha) dF_{S}(t)\right]}L_S(s/\alpha) \right. \nonumber\\
&\quad \left.-\int_0^\infty e^{-(s/\alpha) t} F_Y(t/\alpha) dF_{S}(t)\right],
\end{align}where
 \begin{align}
V(s) = \frac{f}{s+f}[1-L_S(s+f)]\cdot\left[L_D(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_{D}(t)\right].
\end{align}
\begin{align}
V(s) = \frac{f}{s+f}[1-L_S(s+f)]\cdot\left[L_D(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_{D}(t)\right].
\end{align}The proof of Proposition 2.1 is constructive and can be found in detail in Appendix A. A special case of interest is detailed in Corollary 2.2, which is stated without proof.
Corollary 2.2. (Exponential service time)
Assume that the service requirement is exponentially distributed with mean ![]() $1/\mu$. Then, the Laplace–Stieltjes transform of the completion time distribution given in (2.4)–(2.5) reduces to (2.6)–(2.7).
$1/\mu$. Then, the Laplace–Stieltjes transform of the completion time distribution given in (2.4)–(2.5) reduces to (2.6)–(2.7).
 \begin{align}
L_T(s)
&= E\left[e^{-sT}\right] \nonumber \\
&= \dfrac{f}{(f+r)}\frac{\mu\alpha\left[s+\mu\alpha -r(1-L_D(s+\mu\alpha))\right]}{(s+\mu\alpha)^2} \nonumber \\
& \quad + \frac{1}{1-V(s)} \left\{\dfrac{r}{(f+r)}\frac{\mu\left[s+\mu\alpha+f(1+\alpha)(1-L_D(s+\mu\alpha))\right]}{(s+f+\mu)(s+\mu\alpha)}\right.\nonumber\\ &\quad +\left. \dfrac{f}{(f+r)}\frac{fr\mu\alpha\left[1-L_D(s+\mu\alpha)\right]^2}{(s+f+\mu)(s+\mu\alpha)^2}\right\}
\end{align}
\begin{align}
L_T(s)
&= E\left[e^{-sT}\right] \nonumber \\
&= \dfrac{f}{(f+r)}\frac{\mu\alpha\left[s+\mu\alpha -r(1-L_D(s+\mu\alpha))\right]}{(s+\mu\alpha)^2} \nonumber \\
& \quad + \frac{1}{1-V(s)} \left\{\dfrac{r}{(f+r)}\frac{\mu\left[s+\mu\alpha+f(1+\alpha)(1-L_D(s+\mu\alpha))\right]}{(s+f+\mu)(s+\mu\alpha)}\right.\nonumber\\ &\quad +\left. \dfrac{f}{(f+r)}\frac{fr\mu\alpha\left[1-L_D(s+\mu\alpha)\right]^2}{(s+f+\mu)(s+\mu\alpha)^2}\right\}
\end{align}where
 \begin{equation}
V(s) = \frac{f}{s+f+\mu}\cdot L_D(s+\mu\alpha).
\end{equation}
\begin{equation}
V(s) = \frac{f}{s+f+\mu}\cdot L_D(s+\mu\alpha).
\end{equation}The following specialized result for exponential up and down durations was proved by Baykal-Gursoy et al. [Reference Baykal-Gürsoy, Benton, Gerum and Candia5].
Corollary 2.3. (Exponential down periods)
Assume that the down period duration D is exponentially distributed with mean ![]() $1/r$. Then, the Laplace–Stieltjes transform of the completion time distribution given in (2.4)–(2.5) reduces to (2.8)–(2.9).
$1/r$. Then, the Laplace–Stieltjes transform of the completion time distribution given in (2.4)–(2.5) reduces to (2.8)–(2.9).
 \begin{align}
L_T(s)
&= \; E[e^{-sT}] \nonumber \\
&= \; E[e^{-sT}|G^1]P\{G^1\}+E[e^{-sT}|G^2]P\{G^2\} \nonumber \\
&= \; \dfrac{r}{f+r}\cdot\frac{1}{1-V(s)}L_S(s+f)\left(1 +
\frac{f}{s+r}\left[1-L_S\left(\frac{s+r}{\alpha}\right)\right]\right)
\nonumber \\
& \quad + \dfrac{f}{f+r}\cdot\frac{1}{1-V(s)}L_S\left(\frac{s+r}{\alpha}\right)\left(1+
\frac{r}{s+f}\left[1-L_S(s+f)\right]\right),
\end{align}
\begin{align}
L_T(s)
&= \; E[e^{-sT}] \nonumber \\
&= \; E[e^{-sT}|G^1]P\{G^1\}+E[e^{-sT}|G^2]P\{G^2\} \nonumber \\
&= \; \dfrac{r}{f+r}\cdot\frac{1}{1-V(s)}L_S(s+f)\left(1 +
\frac{f}{s+r}\left[1-L_S\left(\frac{s+r}{\alpha}\right)\right]\right)
\nonumber \\
& \quad + \dfrac{f}{f+r}\cdot\frac{1}{1-V(s)}L_S\left(\frac{s+r}{\alpha}\right)\left(1+
\frac{r}{s+f}\left[1-L_S(s+f)\right]\right),
\end{align}where
 \begin{equation}
V(s) = \frac{rf\left[1-L_S(s+f)\right]\left[1-L_S(\frac{s+r}{\alpha})\right]}{(s+f)(s+r)},
\end{equation}
\begin{equation}
V(s) = \frac{rf\left[1-L_S(s+f)\right]\left[1-L_S(\frac{s+r}{\alpha})\right]}{(s+f)(s+r)},
\end{equation}and with mean
 \begin{equation}
E[T] =
\dfrac{
\dfrac{1}{r}(1-L_S(r/\alpha))\left[1 -\dfrac{r}{r+f}L_S(f)\right]+
\dfrac{1}{f}(1-L_S(f))\left[1 -\dfrac{f}{r+f}L_S(r/\alpha)\right]
}{
L_S(r/\alpha)+L_S(f) -L_S(f)L_S(r/\alpha)
}.
\end{equation}
\begin{equation}
E[T] =
\dfrac{
\dfrac{1}{r}(1-L_S(r/\alpha))\left[1 -\dfrac{r}{r+f}L_S(f)\right]+
\dfrac{1}{f}(1-L_S(f))\left[1 -\dfrac{f}{r+f}L_S(r/\alpha)\right]
}{
L_S(r/\alpha)+L_S(f) -L_S(f)L_S(r/\alpha)
}.
\end{equation}Under very special circumstances the completion time distribution Laplace–Stieltjes transform given in (2.8)–(2.9) can be inverted analytically. In general, it is necessary to resort to numerical Laplace inversion methods (see, e.g., [Reference Abate and Whitt1], [Reference Weeks37], [Reference Talbot36]). We have experience with De Hoog’s algorithm [Reference de Hoog12] and found it to be efficient when implemented with accelerated convergence for the continued fraction expansion that is developed by Hollenbeck [Reference Hollenbeck20]. It is worth mentioning that no single method for Laplace transform inversion is guaranteed to give good results as this depends greatly on the specific application [Reference Epstein and Schotland14].
The case in which all random variables, that is, up and down time durations, and service time requirement, are exponential was also discussed in [Reference Baykal-Gürsoy, Benton, Gerum and Candia5].
Corollary 2.4. (Exponential down periods and service times)
Consider the server described in Section 2, assume that the down period duration D is exponentially distributed with mean ![]() $1/r$, and that the service requirement is exponentially distributed with mean
$1/r$, and that the service requirement is exponentially distributed with mean ![]() $1/\mu$. Then, the Laplace–Stieltjes transform of completion time r.v. is given as
$1/\mu$. Then, the Laplace–Stieltjes transform of completion time r.v. is given as
 \begin{equation}
L_T(s) = \frac{\mu}{f+r}\cdot \frac{r(s+f+r+\mu\alpha)+f\alpha(s+f+r+\mu)}{(s+f+\mu)(s+r+\mu\alpha)-fr}.
\end{equation}
\begin{equation}
L_T(s) = \frac{\mu}{f+r}\cdot \frac{r(s+f+r+\mu\alpha)+f\alpha(s+f+r+\mu)}{(s+f+\mu)(s+r+\mu\alpha)-fr}.
\end{equation} Using Eq. (2.11), the completion time T distribution can be written as shown below by defining two random variables, T 1 and ![]() $T_{2},$ which are independent, denoting the completion time of customers arriving during up and down periods, respectively,
$T_{2},$ which are independent, denoting the completion time of customers arriving during up and down periods, respectively,
 \begin{equation}
T = \frac{r}{f+r}T_1+\frac{f}{f+r}T_2.
\end{equation}
\begin{equation}
T = \frac{r}{f+r}T_1+\frac{f}{f+r}T_2.
\end{equation}The density functions of T 1 and T 2 can be obtained in closed form by inverting the Laplace–Stieltjes transform as shown in (2.13)–(2.14),
 \begin{align}
f_{T_1}(t) & = \frac{\mu(s_1+f+r+\mu\alpha)}{s_1-s_2}e^{s_1t}-\frac{\mu(s_2+f+r+\mu\alpha)}{s_1-s_2}e^{s_2t},
\end{align}
\begin{align}
f_{T_1}(t) & = \frac{\mu(s_1+f+r+\mu\alpha)}{s_1-s_2}e^{s_1t}-\frac{\mu(s_2+f+r+\mu\alpha)}{s_1-s_2}e^{s_2t},
\end{align} \begin{align}
f_{T_2}(t) & = \frac{\mu\alpha(s_1+f+r+\mu)}{s_1-s_2}e^{s_1t}-\frac{\mu\alpha(s_2+f+r+\mu)}{s_1-s_2}e^{s_2t},
\end{align}
\begin{align}
f_{T_2}(t) & = \frac{\mu\alpha(s_1+f+r+\mu)}{s_1-s_2}e^{s_1t}-\frac{\mu\alpha(s_2+f+r+\mu)}{s_1-s_2}e^{s_2t},
\end{align}where s 1 and s 2 are the solutions of Eq. (2.15),
and are given in Eqs. (2.16) and (2.17):
 \begin{align}
s_{1} & = \dfrac{-(f+r+\mu(1+\alpha))+\sqrt{(f+r+\mu(1+\alpha))^2-4\mu(\alpha\mu+f\alpha + r)}}{2},
\end{align}
\begin{align}
s_{1} & = \dfrac{-(f+r+\mu(1+\alpha))+\sqrt{(f+r+\mu(1+\alpha))^2-4\mu(\alpha\mu+f\alpha + r)}}{2},
\end{align} \begin{align}
s_{2} & = \dfrac{-(f+r+\mu(1+\alpha))-\sqrt{(f+r+\mu(1+\alpha))^2-4\mu(\alpha\mu+f\alpha + r)}}{2}.
\end{align}
\begin{align}
s_{2} & = \dfrac{-(f+r+\mu(1+\alpha))-\sqrt{(f+r+\mu(1+\alpha))^2-4\mu(\alpha\mu+f\alpha + r)}}{2}.
\end{align} It holds that s 1 and s 2 are both negative real numbers and it is clear that ![]() $s_1\geq s_2$.
$s_1\geq s_2$.
The expected completion time for this case is:
 \begin{equation}
E[T] = \frac{1}{\mu}
\left(1+\dfrac{1-\alpha}{\alpha}\cdot\frac{f}{f+r}\cdot\frac{f+r+\mu}{f+r/\alpha+\mu}\right),
\end{equation}
\begin{equation}
E[T] = \frac{1}{\mu}
\left(1+\dfrac{1-\alpha}{\alpha}\cdot\frac{f}{f+r}\cdot\frac{f+r+\mu}{f+r/\alpha+\mu}\right),
\end{equation} which is higher than the mean service time, ![]() $1/\mu$.
$1/\mu$.
2.1.1. Approximating mean completion time using renewal arguments
As discussed before, renewal arguments provide the probability of server being up in steady state as ![]() $r/(r+f)$, and the probability of server being down as
$r/(r+f)$, and the probability of server being down as ![]() $f/(r+f)$. Then, since the mean completion time in an up period is the mean service time requirement,
$f/(r+f)$. Then, since the mean completion time in an up period is the mean service time requirement, ![]() $1/\mu$, and correspondingly
$1/\mu$, and correspondingly ![]() $1/(\alpha \mu)$ for down periods, one might approximate the mean completion time in steady state as the mixture:
$1/(\alpha \mu)$ for down periods, one might approximate the mean completion time in steady state as the mixture:
 \begin{equation}
\text{SSMM}:= \frac{r}{r+f}\frac{1}{\mu} + \frac{f}{r+f}\frac{1}{\alpha \mu}
\end{equation}
\begin{equation}
\text{SSMM}:= \frac{r}{r+f}\frac{1}{\mu} + \frac{f}{r+f}\frac{1}{\alpha \mu}
\end{equation}with SSMM standing for steady-state mixture mean.
However, we can show that in the Markovian case in which all random periods are exponential, the steady state mixture mean over-estimates the expected completion time. In fact, we can calculate the difference explicitly as in Eq. (2.20) [Reference Baykal-Gürsoy, Benton, Gerum and Candia5]
 \begin{equation}
\text{SSMM} - E[T] = \dfrac{fr(1-\alpha)^2}{\alpha\mu(r+f)(f\alpha+r+\mu\alpha)} \geq 0.
\end{equation}
\begin{equation}
\text{SSMM} - E[T] = \dfrac{fr(1-\alpha)^2}{\alpha\mu(r+f)(f\alpha+r+\mu\alpha)} \geq 0.
\end{equation}It is worth mentioning that the generating function of the completion time for the complete breakdown case (which can be obtained by taking the limit α → 0) coincides with Gaver’s preemptive-repeat-different interruption case [Reference Gaver18].
Figure 2 shows an example of the time domain completion time distribution for exponential service time given in Eqs. (2.13)–(2.14). Here we consider ![]() $1/f = 5 \lt 40 = 1/r$ time units, which corresponds to a system in which failures occur more frequently than repairs. The mean service requirement is
$1/f = 5 \lt 40 = 1/r$ time units, which corresponds to a system in which failures occur more frequently than repairs. The mean service requirement is ![]() $1/\mu = 40$, and we vary α to 0.2, 0.4, 0.6, and 0.8.
$1/\mu = 40$, and we vary α to 0.2, 0.4, 0.6, and 0.8.

Figure 2. Completion time distribution under exponential service requirement.
It is clear that as α decreases the mass of the distribution is increasingly shifted toward the right-tail. In particular, Table 1 shows the expected completion times for different values of α calculated using Eq. (2.18), in time units. The expected completion time increases as the server capacity drops to a smaller proportion, α. We also give the SSMM for comparison.
Table 1. Expected completion time and SSMM for exponential S.

2.2. Preempt-RESTART service discipline
In this case, the service requirement, ![]() $S,$ is sampled once, and every time a state-change occurs the same service requirement is repeated, that is,
$S,$ is sampled once, and every time a state-change occurs the same service requirement is repeated, that is, ![]() $S_n = S$ for
$S_n = S$ for ![]() $n= 1, 2, \ldots$. Thus, given that the service requirement, S = t, the completion time given in Eqs. (2.2) and (A.11) are rewritten for an up period, and a down period as shown in Eqs. (2.21) and (2.22), respectively,
$n= 1, 2, \ldots$. Thus, given that the service requirement, S = t, the completion time given in Eqs. (2.2) and (A.11) are rewritten for an up period, and a down period as shown in Eqs. (2.21) and (2.22), respectively,
 \begin{equation}
\{T| S \approx t, G^1\}=
\begin{cases}
t, & \quad \mbox{event }A_0 \\
X + \sum_{i=2}^{n} U_{i} + \sum_{i=1}^n D_i + t, & \quad \mbox{event }A_n, \quad n = 1,2,\ldots\\
X + \sum_{i=2}^{n+1}U_i+\sum_{i=1}^n D_i+\frac{t}{\alpha}, & \quad \mbox{event }E_n, \quad n = 0,1,2,\ldots, \end{cases}
\end{equation}
\begin{equation}
\{T| S \approx t, G^1\}=
\begin{cases}
t, & \quad \mbox{event }A_0 \\
X + \sum_{i=2}^{n} U_{i} + \sum_{i=1}^n D_i + t, & \quad \mbox{event }A_n, \quad n = 1,2,\ldots\\
X + \sum_{i=2}^{n+1}U_i+\sum_{i=1}^n D_i+\frac{t}{\alpha}, & \quad \mbox{event }E_n, \quad n = 0,1,2,\ldots, \end{cases}
\end{equation} \begin{equation}
\{T| S \approx t, G^2\} =
\begin{cases}
\frac{t}{\alpha}, & \quad \mbox{event }A_0 \\
Y+\sum_{i=2}^nD_i+\sum_{i=1}^{n}U_i+\frac{t}{\alpha}, & \quad \mbox{event }A_n, \quad n = 1,2,\ldots \\
Y+\sum_{i=2}^{n+1}D_i+\sum_{i=1}^nU_i+t, & \quad \mbox{event }E_n, \quad n = 0,1,2,\ldots
\end{cases}
\end{equation}
\begin{equation}
\{T| S \approx t, G^2\} =
\begin{cases}
\frac{t}{\alpha}, & \quad \mbox{event }A_0 \\
Y+\sum_{i=2}^nD_i+\sum_{i=1}^{n}U_i+\frac{t}{\alpha}, & \quad \mbox{event }A_n, \quad n = 1,2,\ldots \\
Y+\sum_{i=2}^{n+1}D_i+\sum_{i=1}^nU_i+t, & \quad \mbox{event }E_n, \quad n = 0,1,2,\ldots
\end{cases}
\end{equation} where X denoting the remaining up time with cdf ![]() $F_X(t)$, tail distribution
$F_X(t)$, tail distribution ![]() $\overline{F_{X}(t)}$, conditional mean
$\overline{F_{X}(t)}$, conditional mean ![]() $\textstyle E(X\vert t)=E\lbrack X\vert X \lt t$, and conditional Laplace–Stieltjes transform
$\textstyle E(X\vert t)=E\lbrack X\vert X \lt t$, and conditional Laplace–Stieltjes transform ![]() $L_X[s|t] = E[e^{-sX}|X \lt t]$.
$L_X[s|t] = E[e^{-sX}|X \lt t]$.
Theorems 2.5–2.8 generalize the results in [Reference Fiorini, Sheahan and Lipsky16, Reference Sheahan, Lipsky, Fiorini and Asmussen34] for the complete breakdown case to the partial breakdown case under the restart preemption strategy. Theorem 2.5 presents the Laplace–Stieltjes transform of the completion time conditioned on the task size, and Theorem 2.8 gives the expected completion time conditioned on the task size. The results are stated for general up and down durations with CDFs ![]() $F_{U}(t)$ and
$F_{U}(t)$ and ![]() $F_{D}(t)$, tail distributions
$F_{D}(t)$, tail distributions ![]() $\overline{F_{U}(t)}$ and
$\overline{F_{U}(t)}$ and  $\overline{F_{D}(\frac{t}{\alpha})}$, and Laplace–Stieltjes transform
$\overline{F_{D}(\frac{t}{\alpha})}$, and Laplace–Stieltjes transform ![]() $L_{U}(s)$ and
$L_{U}(s)$ and ![]() $L_{D}(s)$, respectively.
$L_{D}(s)$, respectively.
Theorem 2.5. The conditional Laplace–Stieltjes transform of the completion time distribution for a task of duration t is
 \begin{align}
L_{T}\left(s|S \approx t\right)
&= \dfrac{1}{(r+f)} \bigl[ re^{-st}\overline{F_{X}(t)} +f e^{-s\frac{t}{\alpha}}\overline{F_{Y}(\frac{t}{\alpha})}\bigr] \nonumber\\
&\quad +
\dfrac{e^{-st}\overline{F_{U}(t)}\bigl[r F_{X}(t)L_{X}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha}) +fF_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha}) \bigr]
}
{(r+f)\bigl[1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})\bigr]} \nonumber \\
& \quad + \dfrac{e^{-s\frac{t}{\alpha}}\overline{F_{D}(\frac{t}{\alpha})} \bigl[rF_{X}(t)L_{X}(s|t) +f F_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha})F_{U}(t) L_{U}(s|t) \bigr] }{(r+f)\bigl[1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})\bigr]} ,
\end{align}
\begin{align}
L_{T}\left(s|S \approx t\right)
&= \dfrac{1}{(r+f)} \bigl[ re^{-st}\overline{F_{X}(t)} +f e^{-s\frac{t}{\alpha}}\overline{F_{Y}(\frac{t}{\alpha})}\bigr] \nonumber\\
&\quad +
\dfrac{e^{-st}\overline{F_{U}(t)}\bigl[r F_{X}(t)L_{X}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha}) +fF_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha}) \bigr]
}
{(r+f)\bigl[1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})\bigr]} \nonumber \\
& \quad + \dfrac{e^{-s\frac{t}{\alpha}}\overline{F_{D}(\frac{t}{\alpha})} \bigl[rF_{X}(t)L_{X}(s|t) +f F_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha})F_{U}(t) L_{U}(s|t) \bigr] }{(r+f)\bigl[1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})\bigr]} ,
\end{align} with ![]() $L_{U}(s|t) \equiv E[e^{-sU} | U \lt t]$ and
$L_{U}(s|t) \equiv E[e^{-sU} | U \lt t]$ and  $L_{D}(s|\frac{t}{\alpha}) \equiv E[e^{-sD} | D \lt \frac{t}{\alpha}]$ denoting the conditional Laplace–Stieltjes transform of the up time and down time distributions, respectively, given that the up and down times end before the completion of a task of duration t.
$L_{D}(s|\frac{t}{\alpha}) \equiv E[e^{-sD} | D \lt \frac{t}{\alpha}]$ denoting the conditional Laplace–Stieltjes transform of the up time and down time distributions, respectively, given that the up and down times end before the completion of a task of duration t.
The proof of Theorem 2.5 can be found in Appendix B.
Remark 2.6. Note that if the up and down durations are exponential, then the conditional Laplace–Stieltjes transform of the completion time distribution for a task of duration t is
 \begin{equation}
E[e^{-sT} | S \approx t] =
\dfrac{
e^{-st}\overline{F_{U}(t)}\bigl[r+fL_{D}(s|\frac{t}{\alpha})F_{D}(\frac{t}{\alpha})\bigr]+
e^{-s\frac{t}{\alpha}}\overline{F_{D}(\frac{t}{\alpha})}\bigl[f+rL_{U}(s|t)F_{U}(t)\bigr]
}{(r+f)\bigl[1-L_{U}(s|t)L_{D}(s|\frac{t}{\alpha})F_{U}(t)F_{D}(\frac{t}{\alpha})\bigr]}.
\end{equation}
\begin{equation}
E[e^{-sT} | S \approx t] =
\dfrac{
e^{-st}\overline{F_{U}(t)}\bigl[r+fL_{D}(s|\frac{t}{\alpha})F_{D}(\frac{t}{\alpha})\bigr]+
e^{-s\frac{t}{\alpha}}\overline{F_{D}(\frac{t}{\alpha})}\bigl[f+rL_{U}(s|t)F_{U}(t)\bigr]
}{(r+f)\bigl[1-L_{U}(s|t)L_{D}(s|\frac{t}{\alpha})F_{U}(t)F_{D}(\frac{t}{\alpha})\bigr]}.
\end{equation}Remark 2.7. Note that the above result also matches the result of Gaver [Reference Gaver18] when the server does not work during down times, that is, α = 0.
Theorem 2.8. The expected completion time for a task of length t is
 \begin{align}
E[T|S \approx t]& = \phantom{+ } \frac{1}{r+f}\bigl[r\bigl( t\overline{F_{X}(t)} + E[X|t] F_X(t)\bigr) + f\bigl(\frac{t}{\alpha}\bigr)\overline{F_{Y}(\frac{t}{\alpha})} + E[Y|\frac{t}{\alpha}]F_{Y}(\frac{t}{\alpha})\bigr)\bigr] \notag\\
& \quad + \dfrac{\bigl[rF_X(t)F_{D}(\frac{t}{\alpha})+fF_{Y}(\frac{t}{\alpha})\bigr]\bigl[t\overline{F_{U}(t)}+ E[U|t]F_{U}(t) \bigr] + \bigl[rF_X(t)+fF_{Y}(\frac{t}{\alpha})F_{U}(t)\bigr] \bigl[\frac{t}{\alpha}\overline{F_{D}(\frac{t}{\alpha})} + E[D|\frac{t}{\alpha}]F_{D}(\frac{t}{\alpha})\bigr] }{
(r+f)\bigl(1-F_{U}(t)F_{D}(\frac{t}{\alpha})\bigr)
}
\end{align}
\begin{align}
E[T|S \approx t]& = \phantom{+ } \frac{1}{r+f}\bigl[r\bigl( t\overline{F_{X}(t)} + E[X|t] F_X(t)\bigr) + f\bigl(\frac{t}{\alpha}\bigr)\overline{F_{Y}(\frac{t}{\alpha})} + E[Y|\frac{t}{\alpha}]F_{Y}(\frac{t}{\alpha})\bigr)\bigr] \notag\\
& \quad + \dfrac{\bigl[rF_X(t)F_{D}(\frac{t}{\alpha})+fF_{Y}(\frac{t}{\alpha})\bigr]\bigl[t\overline{F_{U}(t)}+ E[U|t]F_{U}(t) \bigr] + \bigl[rF_X(t)+fF_{Y}(\frac{t}{\alpha})F_{U}(t)\bigr] \bigl[\frac{t}{\alpha}\overline{F_{D}(\frac{t}{\alpha})} + E[D|\frac{t}{\alpha}]F_{D}(\frac{t}{\alpha})\bigr] }{
(r+f)\bigl(1-F_{U}(t)F_{D}(\frac{t}{\alpha})\bigr)
}
\end{align} with ![]() $E[U|t]\equiv E[U | U \lt t]$,
$E[U|t]\equiv E[U | U \lt t]$, ![]() $E[X|t]\equiv E[X | X \lt t],$
$E[X|t]\equiv E[X | X \lt t],$ ![]() $E[D|\frac{t}{\alpha}] \equiv E[D|D \lt \frac{t}{\alpha}]$, and
$E[D|\frac{t}{\alpha}] \equiv E[D|D \lt \frac{t}{\alpha}]$, and ![]() $E[Y|\frac{t}{\alpha}] \equiv E[Y|D \lt \frac{t}{\alpha}]$ denoting the conditional mean of the up time, remaining up time, down time, and remaining down time distributions, respectively, given that the up and down times end before the completion of a task of duration t.
$E[Y|\frac{t}{\alpha}] \equiv E[Y|D \lt \frac{t}{\alpha}]$ denoting the conditional mean of the up time, remaining up time, down time, and remaining down time distributions, respectively, given that the up and down times end before the completion of a task of duration t.
The proof of Theorem 2.8 can be found in Appendix C.
Remark 2.9. Note that if up and down durations are exponential, then the conditional expectation of the completion for a task of length t is
 \begin{align}
E[T|S \approx t] = & \phantom{+ }
\dfrac{
\bigl(t\overline{F_{U}(t)} + E[U|t]F_{U}(t)\bigr)
\bigl(r + fF_{D}(\frac{t}{\alpha})\bigr)
+
\bigl(\frac{t}{\alpha}\overline{F_{D}(\frac{t}{\alpha})} + E[D|\frac{t}{\alpha}]F_{D}(\frac{t}{\alpha})\bigr)
\bigl(f + rF_{U}(t)\bigr)
}{
(r+f)\bigl(1-F_{U}(t)F_{D}(\frac{t}{\alpha})\bigr)
}.
\end{align}
\begin{align}
E[T|S \approx t] = & \phantom{+ }
\dfrac{
\bigl(t\overline{F_{U}(t)} + E[U|t]F_{U}(t)\bigr)
\bigl(r + fF_{D}(\frac{t}{\alpha})\bigr)
+
\bigl(\frac{t}{\alpha}\overline{F_{D}(\frac{t}{\alpha})} + E[D|\frac{t}{\alpha}]F_{D}(\frac{t}{\alpha})\bigr)
\bigl(f + rF_{U}(t)\bigr)
}{
(r+f)\bigl(1-F_{U}(t)F_{D}(\frac{t}{\alpha})\bigr)
}.
\end{align}The Laplace–Stieltjes transform and mean completion time r.v., T, can be derived by unconditioning the respective equations (2.23 and 2.25), with respect to the task size, S, that is,
 \begin{equation*} L_T (s) = \int_{t=0}^{\infty} L_{T}(s|S \approx t) dF_S (t), \end{equation*}
\begin{equation*} L_T (s) = \int_{t=0}^{\infty} L_{T}(s|S \approx t) dF_S (t), \end{equation*} \begin{equation*} E[T] = \int_{t=0}^{\infty} E[T|S \approx t] dF_S (t).\end{equation*}
\begin{equation*} E[T] = \int_{t=0}^{\infty} E[T|S \approx t] dF_S (t).\end{equation*}3. Tail behavior of the completion time
We now present some asymptotic properties of the completion time. This amounts to studying the characteristics of the distribution’s right-tail. The right-tail defines the probability of observing abnormally large completion times, and it is calculated as the complementary cumulative distribution, as shown in (3.1)
 \begin{equation}
\bar{F}_{T}(t) = \mathbb{P}(T \gt t) = 1-F_{T}(t) = 1- \int_{0}^{t}f_{T}(u)du.
\end{equation}
\begin{equation}
\bar{F}_{T}(t) = \mathbb{P}(T \gt t) = 1-F_{T}(t) = 1- \int_{0}^{t}f_{T}(u)du.
\end{equation}We again separate the REPLACE and RESTART cases. We briefly discuss the first case and give some general insights of the tail behavior. For the second case, we derive more specific results on the asymptotic classification.
3.1. Repeat different/REPLACE
For the exponential down periods case, the Laplace transform of the tail can be given explicitly as shown in Eq. (3.2)
 \begin{align}
\mathcal{L}[\bar{F}_T](s) =
& \phantom{\,+\,}
\dfrac{r}{(r+f)}
\dfrac{
\left(1-L_S(s+f)\right)
\left[s +r +f\left(1-L_S\bigl((s+r)/\alpha\bigr)\right)\right]
}
{\left[(s+f)(s+r) -rf(1-L_S(s+f))\left(1-L_S\bigl((s+r)/\alpha\bigr)\right)\right]}
\nonumber \\
& +
\dfrac{f}{(r+f)}
\dfrac{
\left(1-L_S\bigl((s+r)/\alpha\bigr)\right)
\left[s +f +r(1-L_S(s+f))\right]
}
{\left[(s+f)(s+r) -rf(1-L_S(s+f))\left(1-L_S\bigl((s+r)/\alpha\bigr)\right)\right]},
\end{align}
\begin{align}
\mathcal{L}[\bar{F}_T](s) =
& \phantom{\,+\,}
\dfrac{r}{(r+f)}
\dfrac{
\left(1-L_S(s+f)\right)
\left[s +r +f\left(1-L_S\bigl((s+r)/\alpha\bigr)\right)\right]
}
{\left[(s+f)(s+r) -rf(1-L_S(s+f))\left(1-L_S\bigl((s+r)/\alpha\bigr)\right)\right]}
\nonumber \\
& +
\dfrac{f}{(r+f)}
\dfrac{
\left(1-L_S\bigl((s+r)/\alpha\bigr)\right)
\left[s +f +r(1-L_S(s+f))\right]
}
{\left[(s+f)(s+r) -rf(1-L_S(s+f))\left(1-L_S\bigl((s+r)/\alpha\bigr)\right)\right]},
\end{align} where ![]() $L_{S}(\cdot)$ is the Laplace–Stieltjes transform of the service time requirement. In general, the Laplace transform in (3.2) has to be obtained numerically.
$L_{S}(\cdot)$ is the Laplace–Stieltjes transform of the service time requirement. In general, the Laplace transform in (3.2) has to be obtained numerically.
More generally, it can be shown via the counting argument in the proof of Proposition 2.1 (see Eqs. (A.3) and (A.11)), that T is a stochastic sum of the up and down period random variables (U, D) and the service time requirement random variable (S). Then, it suffices for the D or S to be heavy tailed for T to be heavy tailed [Reference Foss, Korshunov and Zachary17].
3.2. Repeat identical/RESTART
In order to analyze the asymptotic behavior of the completion time, one needs to consider the following function for an r.v. C with support contained in ![]() $[0,+\infty)$ and distribution
$[0,+\infty)$ and distribution ![]() $F_{C}(t)$:
$F_{C}(t)$:
 \begin{equation}
\phi(\theta;C) := \int_{0}^{\infty}e^{\theta t}dF_{C}(t).
\end{equation}
\begin{equation}
\phi(\theta;C) := \int_{0}^{\infty}e^{\theta t}dF_{C}(t).
\end{equation} Let ![]() $\theta_{\text{min}}(C) := \sup\{\,\theta\,|\,\phi(\theta;C) \lt \infty\}$. Using this definition, we can classify any distribution function on having finite range, a light tail, an exponential tail, or a heavy tail. This corresponds to the cases of finite support,
$\theta_{\text{min}}(C) := \sup\{\,\theta\,|\,\phi(\theta;C) \lt \infty\}$. Using this definition, we can classify any distribution function on having finite range, a light tail, an exponential tail, or a heavy tail. This corresponds to the cases of finite support, ![]() $\theta_{\text{min}}(C) = \infty$,
$\theta_{\text{min}}(C) = \infty$, ![]() $0 \lt \theta_{\text{min}}(C) \lt \infty$, and
$0 \lt \theta_{\text{min}}(C) \lt \infty$, and ![]() $\theta_{\text{min}}(C) = 0$, respectively [Reference Sheahan, Lipsky, Fiorini and Asmussen34]. We write
$\theta_{\text{min}}(C) = 0$, respectively [Reference Sheahan, Lipsky, Fiorini and Asmussen34]. We write ![]() $\theta_{\text{min}}$ when there is no ambiguity on the r.v. C.
$\theta_{\text{min}}$ when there is no ambiguity on the r.v. C.
Theorem 3.1 shows conditions under which the completion time distribution is power tailed.
Theorem 3.1. Let U and D be exponentially distributed with failure rate f and repair rate r, and call ![]() $\Delta = \min\{f,r/\alpha\}$. Assume that the service-time requirement (task size) has an exponential tail, that is:
$\Delta = \min\{f,r/\alpha\}$. Assume that the service-time requirement (task size) has an exponential tail, that is: ![]() $0 \lt \theta_{\text{min}}(S) = \mu \lt \infty$, and denote
$0 \lt \theta_{\text{min}}(S) = \mu \lt \infty$, and denote ![]() $\varepsilon := \theta_{\text{min}}(S)/\Delta = \mu/\min\{f,r/\alpha\}$. Then,
$\varepsilon := \theta_{\text{min}}(S)/\Delta = \mu/\min\{f,r/\alpha\}$. Then,
and the completion time has power tail,
 \begin{equation}
\bar{F}_{T}(t) \sim \dfrac{c}{t^{\varepsilon}}.
\end{equation}
\begin{equation}
\bar{F}_{T}(t) \sim \dfrac{c}{t^{\varepsilon}}.
\end{equation}The proof of Theorem 3.1 is shown in Appendix D.
We note that the tail behavior of completion times depends on the ratio of the maximum of the means of up time and the speed adjusted down time, with the mean task time. If the mean task time is close to the larger mean then all moments of the completion time are undefined. The details of this derivation can be found in the proof of Theorem 3.1 in Appendix D.
Although the preemptive-replace and preemptive-repeat service disciplines seem similar, their tail behaviors are quite different. This happens because in the preemptive-replace case service interruptions may decrease the completion time over what it would be in the preemptive-repeat case, since each service change brings a new task that may have shorter time requirement. In a sense, these interruptions may terminate tasks that require longer time requirement, thus shortening the completion time [Reference Gaver18].
4. An application: insensitivity of the stationary first order moments for infinite server queues with two-state MSP
Several different queueing systems with service degradation can be defined by using the completion time model described above as a generally distributed service time. Next we discuss a model having Poisson arrivals with parameter λ and infinitely many servers of ![]() $M/G/\infty$ type.
$M/G/\infty$ type.
With exponential up and down periods, the process controlling the service rate is a two-state continuous-time Markov chain, independent of the arrival process, and is considered as the external environment. In the case of multiple servers, if all servers are controlled simultaneously, which means that interruptions occur system-wide then the queue is said to have an MSP. On the other hand, similar interruption processes may affect each server independently. These interruptions are assumed to be of preemptive-replace type.
In the case of finitely many servers, system-wide partial failures, and exponential task times, the system becomes the ![]() $\text{M/MSP/c}$ queue analyzed in [Reference Baykal-Gürsoy and Duan6] with two service states. The independent server breakdown case is studied by Mitrany and Avi-Itzhak [Reference Mitrany and Avi-Itzhak27].
$\text{M/MSP/c}$ queue analyzed in [Reference Baykal-Gürsoy and Duan6] with two service states. The independent server breakdown case is studied by Mitrany and Avi-Itzhak [Reference Mitrany and Avi-Itzhak27].
In the case of infinitely many servers, system-wide partial failures, and exponential task time distribution, the system coincides with the ![]() $\text{M/MSP/}\infty$ queue considered in [Reference Baykal-Gürsoy and Xiao7]. Baykal-Gürsoy and Xiao [Reference Baykal-Gürsoy and Xiao7] show that the steady-state number in the system, N, is the sum of two independent random variables: a Poisson r.v. representing the stationary number of customers in an uninterrupted
$\text{M/MSP/}\infty$ queue considered in [Reference Baykal-Gürsoy and Xiao7]. Baykal-Gürsoy and Xiao [Reference Baykal-Gürsoy and Xiao7] show that the steady-state number in the system, N, is the sum of two independent random variables: a Poisson r.v. representing the stationary number of customers in an uninterrupted ![]() $\text{M/G/}\infty$ system, and a randomized Poisson r.v. representing the extra customers accumulated during interruptions. Then, the mean steady-state number of customers in the system is derived as
$\text{M/G/}\infty$ system, and a randomized Poisson r.v. representing the extra customers accumulated during interruptions. Then, the mean steady-state number of customers in the system is derived as
 \begin{equation}
E[N] = \frac{\lambda}{\mu}+\frac{\lambda f(1-\alpha)}{f+r}\cdot \frac{f+r+\mu}{\mu(f\alpha+r+\mu\alpha)}.
\end{equation}
\begin{equation}
E[N] = \frac{\lambda}{\mu}+\frac{\lambda f(1-\alpha)}{f+r}\cdot \frac{f+r+\mu}{\mu(f\alpha+r+\mu\alpha)}.
\end{equation} On the other hand, assuming that there are no jockeying between the servers, one can analyze the independent server interruption case similar to an ![]() $\text{M/G/}\infty$ system as will be discussed below.
$\text{M/G/}\infty$ system as will be discussed below.
When Markovian service interruptions arrive independently to each of the infinitely many servers, a job joining the system experiences exactly the same task completion time derived in Corollary 2.3. Each task completion time is independent and identically distributed. Hence, this system becomes an ![]() $\text{M/G/}\infty$ system with the service time equal to the completion time, T, that is given in the frequency domain by Eqs. (2.8) and (2.9).
$\text{M/G/}\infty$ system with the service time equal to the completion time, T, that is given in the frequency domain by Eqs. (2.8) and (2.9).
Clearly, the stationary number of customers in the ![]() $\text{M/G/}\infty$ queue is Poisson distributed with parameter
$\text{M/G/}\infty$ queue is Poisson distributed with parameter ![]() $\rho = \lambda \cdot E[T]$. Hence, the expected number of customers in the system, N, using the expected completion time from Eq. (2.18) is given as in (4.1) (see Eq. (3.6) in [Reference Baykal-Gürsoy and Xiao7]).
$\rho = \lambda \cdot E[T]$. Hence, the expected number of customers in the system, N, using the expected completion time from Eq. (2.18) is given as in (4.1) (see Eq. (3.6) in [Reference Baykal-Gürsoy and Xiao7]).
The expected system time for this system, that is, the job completion time, in turn coincides with the mean system time for the ![]() $\text{M/MSP/}\infty$ queue obtained via Little’s law from Eq. (4.1) as
$\text{M/MSP/}\infty$ queue obtained via Little’s law from Eq. (4.1) as ![]() $E[T] = E[N]/\lambda$. For the
$E[T] = E[N]/\lambda$. For the ![]() $\text{M/MSP/}\infty$ queue in [Reference Baykal-Gürsoy and Xiao7], however, the steady-state variance of the number in the system is not equal to its expected value, which has to be the case in the
$\text{M/MSP/}\infty$ queue in [Reference Baykal-Gürsoy and Xiao7], however, the steady-state variance of the number in the system is not equal to its expected value, which has to be the case in the ![]() $\text{M/G/}\infty$ setting with independent server failures and preempt-replace service discipline. Thus, except the first order moments, the higher moments do not match in the case of system wide interruptions with the interruptions affecting each server independently.
$\text{M/G/}\infty$ setting with independent server failures and preempt-replace service discipline. Thus, except the first order moments, the higher moments do not match in the case of system wide interruptions with the interruptions affecting each server independently.
5. Conclusion
We study the task completion time of a server experiencing randomly occurring service deterioration. Focusing on preempt-replace and preempt-repeat service recovery disciplines following each service interruption, we derive the Laplace–Stieltjes transform of the task completion times using counting arguments. We observe that in general the resulting distributions are difficult to obtain explicitly in the time domain and one has to resort to numerical inversion of the transforms. For the specific case of exponential down period and exponential task time case we can determine the exact form of the completion time. Furthermore, we show how the steady-state mixture can be compared against the expected completion time, which can be useful for applications in which a simpler steady state model is preferred.
The analysis of the tail distribution demonstrates that in the preempt-repeat service discipline even when the task time distribution has exponential tail, the completion time distribution may have power tail. Our results provide conditions under which the moments of the completion time exist. Moreover, the connection between the expected task completion time presented in this study and the expected system time for the ![]() $\text{M/MSP/}\infty$ queue studied by Baykal-Gürsoy and Xiao [Reference Baykal-Gürsoy and Xiao7], reveals that the first order moments at an infinite server queue in random environment are insensitive to how the random environment affects the servers.
$\text{M/MSP/}\infty$ queue studied by Baykal-Gürsoy and Xiao [Reference Baykal-Gürsoy and Xiao7], reveals that the first order moments at an infinite server queue in random environment are insensitive to how the random environment affects the servers.
Acknowledgments
The first author is grateful to Xiuli Chao and Mert Gürbüzbalaban for fruitful discussions. The authors thank two anonymous referees and the Associate Editor, Lerzan Örmeci for their helpful comments and suggestions to improve this manuscript. The second author is supported by the Chilean Fulbright Commission during his PhD studies. His research was also partly funded by the Tayfur Altiok Scholarship of the Industrial & Systems Engineering Department, Rutgers University.
Appendix A. Proof of Proposition 2.1
As mentioned before, we condition the completion time on the epoch that work starts on a task. Let G 1 denote the event in which work starts during an up period, and G 2 the event in which work starts during a down period. Then the occurrence probabilities of events G 1 and G 2 are given by Eq. (2.1). The Laplace–Stieltjes transform of conditional completion time is calculated separately for each one of these events and then unconditioned.
Consider the case that work starts during an up period, and denote the subsequent up and down periods as Ui and Di, respectively, for ![]() $i=1,2,3,\ldots$. The task time at each period is denoted as Si,
$i=1,2,3,\ldots$. The task time at each period is denoted as Si, ![]() $i=1,2,3,\ldots$. Refer to Figure 1 for a sample path of how the system could evolve. Define the following events:
$i=1,2,3,\ldots$. Refer to Figure 1 for a sample path of how the system could evolve. Define the following events:
• An, for
 $n=0,1,2,\ldots$. There are n complete up and down periods, and another incomplete up period in the completion time. In general, A denotes the case that the work on a task starts and ends at the same regime. In G 1, work starts while the server is up. The second cross in Figure 1 is an example of event A 2. Notice that the occurrence of event An implies that necessarily:
$n=0,1,2,\ldots$. There are n complete up and down periods, and another incomplete up period in the completion time. In general, A denotes the case that the work on a task starts and ends at the same regime. In G 1, work starts while the server is up. The second cross in Figure 1 is an example of event A 2. Notice that the occurrence of event An implies that necessarily:(1)
 $S_{2i-1} \gt U_i$, for all
$S_{2i-1} \gt U_i$, for all  $i=1,2,\ldots,n$,
$i=1,2,\ldots,n$,(2)
 $\frac{1}{\alpha}S_{2i} \gt D_i$, for all
$\frac{1}{\alpha}S_{2i} \gt D_i$, for all  $i=1,2,\ldots,n$,
$i=1,2,\ldots,n$,(3)
 $S_{2n+1} \lt U_{n+1}$.
$S_{2n+1} \lt U_{n+1}$.
• En, for
 $n=0,1,2,\ldots$. There are n + 1 complete up and n complete down periods, and another incomplete down period in the completion time. In general, E denotes the case that the work on a task starts and ends at different regimes. The first cross in Figure 1 is an example of event E 1. Here, necessarily:
$n=0,1,2,\ldots$. There are n + 1 complete up and n complete down periods, and another incomplete down period in the completion time. In general, E denotes the case that the work on a task starts and ends at different regimes. The first cross in Figure 1 is an example of event E 1. Here, necessarily:(1)
 $S_{2i-1} \gt U_i$, for all
$S_{2i-1} \gt U_i$, for all  $i=1,2,\ldots,n+1$,
$i=1,2,\ldots,n+1$,(2)
 $\frac{1}{\alpha}S_{2i} \gt D_i$, for all
$\frac{1}{\alpha}S_{2i} \gt D_i$, for all  $i=1,2,\ldots,n$,
$i=1,2,\ldots,n$,(3)
 $\frac{1}{\alpha}S_{2n+2} \lt D_{n+1}$.
$\frac{1}{\alpha}S_{2n+2} \lt D_{n+1}$.
Since clearly events Si, Ui, and Di, are independent and respectively identically distributed for all i, then for all ![]() $n=0,1,2,\ldots$
$n=0,1,2,\ldots$
 \begin{align}
P\left\{A_n|G^1\right\}&=P^n\{S \gt U\}\cdot P^n\{S \gt \alpha D\}\cdot P\{S \lt U\},
\end{align}
\begin{align}
P\left\{A_n|G^1\right\}&=P^n\{S \gt U\}\cdot P^n\{S \gt \alpha D\}\cdot P\{S \lt U\},
\end{align} \begin{align}
P\left\{E_n|G^1\right\}&=P^{n+1}\{S \gt U\}\cdot P^n\{(1/\alpha) S \gt D\}\cdot P\{(1/\alpha) S \lt D\}.
\end{align}
\begin{align}
P\left\{E_n|G^1\right\}&=P^{n+1}\{S \gt U\}\cdot P^n\{(1/\alpha) S \gt D\}\cdot P\{(1/\alpha) S \lt D\}.
\end{align} Notice that the probabilities defined in (A.1)–(A.2) were obtained by simple enumeration of the number of state transitions. Then, as already stated in Eq. (2.2), the conditional completion time ![]() $\{T| G^1\}$ under each event stated above is
$\{T| G^1\}$ under each event stated above is
 \begin{equation}
\{T| G^1\}=
\begin{cases}
\sum_{i=1}^{n}\left(U_{i} + D_i\right) + S_{2n+1}, & \quad \mbox{event }A_n,\\
\sum_{i=1}^{n+1}U_i+\sum_{i=1}^n D_i+\frac{1}{\alpha}S_{2n+2}, & \quad \mbox{event }E_n,
\end{cases}
\quad
n = 0,1,2,\ldots.
\end{equation}
\begin{equation}
\{T| G^1\}=
\begin{cases}
\sum_{i=1}^{n}\left(U_{i} + D_i\right) + S_{2n+1}, & \quad \mbox{event }A_n,\\
\sum_{i=1}^{n+1}U_i+\sum_{i=1}^n D_i+\frac{1}{\alpha}S_{2n+2}, & \quad \mbox{event }E_n,
\end{cases}
\quad
n = 0,1,2,\ldots.
\end{equation}In order to specify the conditional completion time Laplace–Stieltjes transform under some event H, we use the indicator variable for H defined as
 \begin{equation*}
\mathbf{1}\{H\} =
\begin{cases}
1, & \quad \mbox{event } H,\\
0, & \quad \mbox{otherwise}
\end{cases}
\end{equation*}
\begin{equation*}
\mathbf{1}\{H\} =
\begin{cases}
1, & \quad \mbox{event } H,\\
0, & \quad \mbox{otherwise}
\end{cases}
\end{equation*} then, for all ![]() $n=0,1,2,\ldots$
$n=0,1,2,\ldots$
 \begin{align}
E[e^{-sT} \mathbf{1}\{A_n\} | G^1] &= E[e^{-sT}|A_n,G^1]\cdot P\{A_n|G^1\} \nonumber\\
&=\left(E[e^{-sU}|S \gt U]P\{S \gt U\}\right)^n\left(E[e^{-sD}|S \gt \alpha D]P\{S \gt \alpha D\}\right)^n \nonumber\\
&\quad \times E[e^{-sS}|S \lt U]P\{S \lt U\},
\end{align}
\begin{align}
E[e^{-sT} \mathbf{1}\{A_n\} | G^1] &= E[e^{-sT}|A_n,G^1]\cdot P\{A_n|G^1\} \nonumber\\
&=\left(E[e^{-sU}|S \gt U]P\{S \gt U\}\right)^n\left(E[e^{-sD}|S \gt \alpha D]P\{S \gt \alpha D\}\right)^n \nonumber\\
&\quad \times E[e^{-sS}|S \lt U]P\{S \lt U\},
\end{align}where s is a complex number with positive real part, ![]() $U\sim\text{Exp}(f)$, S denotes the generally distributed task time random variable under normal conditions, and D is the generally distributed down period random variable.
$U\sim\text{Exp}(f)$, S denotes the generally distributed task time random variable under normal conditions, and D is the generally distributed down period random variable.
The Laplace–Stieltjes transform of the up period for up times lasting less than the service requirement is derived below as
 \begin{align}
E[e^{-sU}|S \gt U]P\{S \gt U\}
& =
E[e^{-sU} \mathbf{1}\{S \gt U\}] = \int_{x=0}^\infty \int_{u=0}^x e^{-su} f e^{-fu} du\; dF_{S}(x) \nonumber\\
& =
\frac{f}{s+f} - \int_{u=0}^\infty f e^{-(s+f)u} F_{S}(u)\; du = \frac{f}{s+f}[1-L_S(s+f)].
\end{align}
\begin{align}
E[e^{-sU}|S \gt U]P\{S \gt U\}
& =
E[e^{-sU} \mathbf{1}\{S \gt U\}] = \int_{x=0}^\infty \int_{u=0}^x e^{-su} f e^{-fu} du\; dF_{S}(x) \nonumber\\
& =
\frac{f}{s+f} - \int_{u=0}^\infty f e^{-(s+f)u} F_{S}(u)\; du = \frac{f}{s+f}[1-L_S(s+f)].
\end{align}The last equality follows directly from the properties of Laplace–Stieltjes transform or by application of integration by parts to the integral term. Similarly, the following holds
 \begin{align}
& E[e^{-sD}|S \gt \alpha D]P\{S \gt \alpha D\} = L_D(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_{D}(t),
\end{align}
\begin{align}
& E[e^{-sD}|S \gt \alpha D]P\{S \gt \alpha D\} = L_D(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_{D}(t),
\end{align} By substituting Eqs. (A.5)–(A.7) into (A.4), the conditional Laplace–Stieltjes transform can be written for all ![]() $n=0,1,2,\ldots$ as
$n=0,1,2,\ldots$ as
 \begin{equation}
E[e^{-sT} \mathbf{1}\{A_n\}|G^1] = \left\{\frac{f}{s+f}[1-L_S(s+f)]\right\}^n\cdot\left\{L_D(s)-\int_0^\infty e^{-st}F_S(\alpha t) dF_{D}(t)\right\}^n L_S(s+f).
\end{equation}
\begin{equation}
E[e^{-sT} \mathbf{1}\{A_n\}|G^1] = \left\{\frac{f}{s+f}[1-L_S(s+f)]\right\}^n\cdot\left\{L_D(s)-\int_0^\infty e^{-st}F_S(\alpha t) dF_{D}(t)\right\}^n L_S(s+f).
\end{equation} Similarly for events En, we have for all ![]() $n=0,1,2,\ldots$
$n=0,1,2,\ldots$
 \begin{multline*}
E[e^{-sT} \mathbf{1}\{E_n\} | G^1] = E[e^{-sT}|E_n,G^1]\cdot P\{E_n|G^1\} \\
=
\left(E[e^{-sU}|S \gt U]P\{S \gt U\}\right)^{n+1}
\left(E[e^{-sD}|S \gt \alpha D]P\{S \gt \alpha D\}\right)^n
E[e^{-s\frac{1}{\alpha}S}|S \lt \alpha D]P\{S \lt \alpha D\},
\end{multline*}
\begin{multline*}
E[e^{-sT} \mathbf{1}\{E_n\} | G^1] = E[e^{-sT}|E_n,G^1]\cdot P\{E_n|G^1\} \\
=
\left(E[e^{-sU}|S \gt U]P\{S \gt U\}\right)^{n+1}
\left(E[e^{-sD}|S \gt \alpha D]P\{S \gt \alpha D\}\right)^n
E[e^{-s\frac{1}{\alpha}S}|S \lt \alpha D]P\{S \lt \alpha D\},
\end{multline*}where the last term can be derived as
 \begin{align*}
E[e^{-s\frac{1}{\alpha}S}|S \lt \alpha D]P\{S \lt \alpha D\} &= E[e^{-s\frac{1}{\alpha}S}\mathbf{1}\{S \lt \alpha D\}] \\
&= \int_{t=0}^\infty \int_{x=0}^{\alpha t} e^{- \frac{s}{\alpha} x} dF_S(x) dF_D(t) = \int_{x=0}^\infty \left\{\int_{t=\frac{x}{\alpha}}^\infty dF_D(t) \right\} e^{- \frac{s}{\alpha} x} dF_S(x) \\
&= \int_{x=0}^\infty e^{- \frac{s}{\alpha} x} \left(1-F_D\left(\frac{x}{\alpha}\right)\right) dF_S(x) = L_S\left(\frac{s}{\alpha}\right) - \int_{x=0}^\infty e^{- \frac{s}{\alpha} x} F_D\left(\frac{x}{\alpha}\right) dF_S(x)
\end{align*}
\begin{align*}
E[e^{-s\frac{1}{\alpha}S}|S \lt \alpha D]P\{S \lt \alpha D\} &= E[e^{-s\frac{1}{\alpha}S}\mathbf{1}\{S \lt \alpha D\}] \\
&= \int_{t=0}^\infty \int_{x=0}^{\alpha t} e^{- \frac{s}{\alpha} x} dF_S(x) dF_D(t) = \int_{x=0}^\infty \left\{\int_{t=\frac{x}{\alpha}}^\infty dF_D(t) \right\} e^{- \frac{s}{\alpha} x} dF_S(x) \\
&= \int_{x=0}^\infty e^{- \frac{s}{\alpha} x} \left(1-F_D\left(\frac{x}{\alpha}\right)\right) dF_S(x) = L_S\left(\frac{s}{\alpha}\right) - \int_{x=0}^\infty e^{- \frac{s}{\alpha} x} F_D\left(\frac{x}{\alpha}\right) dF_S(x)
\end{align*}giving for all ![]() $n=0,1,2,\ldots$
$n=0,1,2,\ldots$
 \begin{align*}
E[e^{-sT} \mathbf{1}\{E_n\} | G^1] =
\left\{\frac{f}{s+f}[1-L_S(s+f)]\right\}^{n+1}\cdot \left\{L_D(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_D(t) \right\}^n
\end{align*}
\begin{align*}
E[e^{-sT} \mathbf{1}\{E_n\} | G^1] =
\left\{\frac{f}{s+f}[1-L_S(s+f)]\right\}^{n+1}\cdot \left\{L_D(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_D(t) \right\}^n
\end{align*} \begin{align}
\cdot \left[ L_S\left(\frac{s}{\alpha}\right) - \int_{x=0}^\infty e^{- \frac{s}{\alpha} x} F_D\left(\frac{x}{\alpha}\right) dF_S(x)\right].
\end{align}
\begin{align}
\cdot \left[ L_S\left(\frac{s}{\alpha}\right) - \int_{x=0}^\infty e^{- \frac{s}{\alpha} x} F_D\left(\frac{x}{\alpha}\right) dF_S(x)\right].
\end{align}Then, from (A.8) and (A.9), we obtain the Laplace–Stieltjes transform of the conditional completion time, given that the work starts during up period as shown in (A.10)
 \begin{align}
E\bigl[e^{-sT}|G^1\bigr] & = \sum_{n=0}^\infty E\left[e^{-sT}|A_n,G^1\right]P\{A_n|G^1\}+\sum_{n=0}^\infty E\left[e^{-sC}|E_n,G^1\right]P\{E_n|G^1\} \nonumber \\
& = \frac{1}{1-V(s)}\cdot \left\{L_S(s+f)+\frac{f}{s+f}\cdot [1-L_S(s+f)] \cdot \left[L_S\left(\frac{s}{\alpha}\right) - \int_{x=0}^\infty e^{- \frac{s}{\alpha} x} F_D\left(\frac{x}{\alpha}\right) dF_S(x)\right]\right\},
\end{align}
\begin{align}
E\bigl[e^{-sT}|G^1\bigr] & = \sum_{n=0}^\infty E\left[e^{-sT}|A_n,G^1\right]P\{A_n|G^1\}+\sum_{n=0}^\infty E\left[e^{-sC}|E_n,G^1\right]P\{E_n|G^1\} \nonumber \\
& = \frac{1}{1-V(s)}\cdot \left\{L_S(s+f)+\frac{f}{s+f}\cdot [1-L_S(s+f)] \cdot \left[L_S\left(\frac{s}{\alpha}\right) - \int_{x=0}^\infty e^{- \frac{s}{\alpha} x} F_D\left(\frac{x}{\alpha}\right) dF_S(x)\right]\right\},
\end{align}where
 \begin{equation*}
V(s) = \frac{f}{s+f}[1-L_S(s+f)]\cdot\left[L_D(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_D(t)\right].
\end{equation*}
\begin{equation*}
V(s) = \frac{f}{s+f}[1-L_S(s+f)]\cdot\left[L_D(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_D(t)\right].
\end{equation*}Consider now that work starts during down period, that is, under G 2. Figure A1 shows a sample path of a run for the system when work starts during down period.

Figure A1. Sample path of service system under G 2.
Remember that we denote by Y the remaining down time after work starts. Let, again, An denote the case that the work on a task starts and ends while the server is down, and there are n up and n down periods with one of them being the remaining down time, and one incomplete down time. Similarly, let En denote the case that the work starts while the server is down and ends while the server is up, and there are ![]() $(n+1)$ down periods and n up period with an incomplete up period. Then, the conditional completion time given that work starts during a down period will be
$(n+1)$ down periods and n up period with an incomplete up period. Then, the conditional completion time given that work starts during a down period will be
 \begin{equation}
\{T|G^2\}=
\begin{cases}
\frac{1}{\alpha}S_1, & \quad \mbox{event }A_0 \\
Y+\sum_{i=2}^nD_i+\sum_{i=1}^{n}U_i+\frac{1}{\alpha}S_{2n+1}, & \quad \mbox{event }A_n, \quad n = 1,2,\ldots \\
Y+\sum_{i=2}^{n+1}D_i+\sum_{i=1}^nU_i+S_{2n+2}, & \quad \mbox{event }E_n, \quad n = 0,1,2,\ldots.
\end{cases}
\end{equation}
\begin{equation}
\{T|G^2\}=
\begin{cases}
\frac{1}{\alpha}S_1, & \quad \mbox{event }A_0 \\
Y+\sum_{i=2}^nD_i+\sum_{i=1}^{n}U_i+\frac{1}{\alpha}S_{2n+1}, & \quad \mbox{event }A_n, \quad n = 1,2,\ldots \\
Y+\sum_{i=2}^{n+1}D_i+\sum_{i=1}^nU_i+S_{2n+2}, & \quad \mbox{event }E_n, \quad n = 0,1,2,\ldots.
\end{cases}
\end{equation}The pdf of the remaining down time Y is
and its Laplace–Stieltjes transform is
 \begin{align}
L_Y(s)=\frac{r}{s}[1-L_D(s)].
\end{align}
\begin{align}
L_Y(s)=\frac{r}{s}[1-L_D(s)].
\end{align}We write the Laplace–Stieltjes transform of the conditional completion time under each event as
 \begin{align}
& E[e^{-sT} \mathbf{1}\{A_0\} | G^2] = E[e^{-sT}|A_0,G^2]\cdot P\{A_0|G^2\} = L_S\left(s/\alpha\right)-\int_0^\infty e^{-\frac{s}{\alpha}t}F_Y\left(t/\alpha\right) dF_S(t) ,
\end{align}
\begin{align}
& E[e^{-sT} \mathbf{1}\{A_0\} | G^2] = E[e^{-sT}|A_0,G^2]\cdot P\{A_0|G^2\} = L_S\left(s/\alpha\right)-\int_0^\infty e^{-\frac{s}{\alpha}t}F_Y\left(t/\alpha\right) dF_S(t) ,
\end{align} \begin{align}
& E[e^{-sT} \mathbf{1}\{E_0\} | G^2] = E[e^{-sT}|E_0,G^2]\cdot P\{E_0|G^2\} = L_S(s+f)\cdot \left[L_Y(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_Y(t) \right],
\end{align}
\begin{align}
& E[e^{-sT} \mathbf{1}\{E_0\} | G^2] = E[e^{-sT}|E_0,G^2]\cdot P\{E_0|G^2\} = L_S(s+f)\cdot \left[L_Y(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_Y(t) \right],
\end{align}for all ![]() $n=1,2,\ldots$
$n=1,2,\ldots$
 \begin{align}
E[e^{-sT} \mathbf{1}\{A_n\} | G^2] & = E[e^{-sT}|A_n,G^2]\cdot P\{A_n|G^2\} \nonumber \\
& = \left[L_Y(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_Y(t)\right]\cdot
\left[L_D(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_D(t) \right]^{n-1} \cdot
\nonumber\\
& \phantom{=}\,\,\, \left[\frac{f}{s+f} \left(1-L_S(s+f)\right)\right]^n \left[ L_S\left(\frac{s}{\alpha}\right) - \int_{x=0}^\infty e^{- \frac{s}{\alpha} x} F_D\left(\frac{x}{\alpha}\right) dF_S(x)\right],
\end{align}
\begin{align}
E[e^{-sT} \mathbf{1}\{A_n\} | G^2] & = E[e^{-sT}|A_n,G^2]\cdot P\{A_n|G^2\} \nonumber \\
& = \left[L_Y(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_Y(t)\right]\cdot
\left[L_D(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_D(t) \right]^{n-1} \cdot
\nonumber\\
& \phantom{=}\,\,\, \left[\frac{f}{s+f} \left(1-L_S(s+f)\right)\right]^n \left[ L_S\left(\frac{s}{\alpha}\right) - \int_{x=0}^\infty e^{- \frac{s}{\alpha} x} F_D\left(\frac{x}{\alpha}\right) dF_S(x)\right],
\end{align} \begin{align}
E[e^{-sT} \mathbf{1}\{E_n\} | G^2] & = E[e^{-sT}|E_n,G^2]\cdot P\{E_n|G^2\} \nonumber \\
& = \left[L_Y(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_Y(t)\right] \cdot \left[L_D(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_D(t)\right]^{n} \cdot
\nonumber\\
& \phantom{=}\,\,\, \left[\frac{f}{s+f} \left(1-L_S(s+f)\right)\right]^n\cdot L_S(s+f).
\end{align}
\begin{align}
E[e^{-sT} \mathbf{1}\{E_n\} | G^2] & = E[e^{-sT}|E_n,G^2]\cdot P\{E_n|G^2\} \nonumber \\
& = \left[L_Y(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_Y(t)\right] \cdot \left[L_D(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_D(t)\right]^{n} \cdot
\nonumber\\
& \phantom{=}\,\,\, \left[\frac{f}{s+f} \left(1-L_S(s+f)\right)\right]^n\cdot L_S(s+f).
\end{align}Using (A.14)–(A.17), we obtain the Laplace–Stieltjes transform of the conditional completion times as
 \begin{align}
E[e^{-sT}|G^2] = \,\, & \frac{1}{1-V(s)}\cdot \left[L_Y(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_{Y}(t) \right] \cdot \nonumber\\
& \left\{\frac{f}{s+f}[1-L_S(s+f)]\cdot \left[L_S\left(\dfrac{s}{\alpha}\right)-\int_{x=0}^\infty e^{-\frac{s}{\alpha}x} F_D\left(\dfrac{x}{\alpha}\right) dF_{S}(x)\right] + L_S(s+f)\right\}+ \nonumber\\
&\left[L_S\left(\dfrac{s}{\alpha}\right)-\int_0^\infty e^{-\frac{s}{\alpha}t} F_Y\left(\dfrac{t}{\alpha}\right) dF_{S}(t)\right].
\end{align}
\begin{align}
E[e^{-sT}|G^2] = \,\, & \frac{1}{1-V(s)}\cdot \left[L_Y(s)-\int_0^\infty e^{-st} F_S(\alpha t) dF_{Y}(t) \right] \cdot \nonumber\\
& \left\{\frac{f}{s+f}[1-L_S(s+f)]\cdot \left[L_S\left(\dfrac{s}{\alpha}\right)-\int_{x=0}^\infty e^{-\frac{s}{\alpha}x} F_D\left(\dfrac{x}{\alpha}\right) dF_{S}(x)\right] + L_S(s+f)\right\}+ \nonumber\\
&\left[L_S\left(\dfrac{s}{\alpha}\right)-\int_0^\infty e^{-\frac{s}{\alpha}t} F_Y\left(\dfrac{t}{\alpha}\right) dF_{S}(t)\right].
\end{align}Finally, by combining the conditional completion times (A.10) and (A.18) using the corresponding probabilities ![]() $P\{G^1\}$ and
$P\{G^1\}$ and ![]() $P\{G^2\}$, the unconditional completion time Laplace–Stieltjes transform is obtained as shown in (2.4)–(2.5).
$P\{G^2\}$, the unconditional completion time Laplace–Stieltjes transform is obtained as shown in (2.4)–(2.5).
Appendix B. Proof of Theorem 2.5
We aim to obtain the conditional Laplace–Stieltjes transform of the completion time distribution for a service time requirement of size t, so we set S ≈ t. From here, the completion time for work starting during an up period is as given in Eq. (2.21) with probabilities
 \begin{align}
P\bigl\{A_n|S \approx t, G^1\bigr\} &=
\begin{cases}
\overline{F_X(t)}, & \quad n=0 \\
F_X(t)\left(F_{U}(t) F_{D}(\frac{t}{\alpha})\right)^{n-1}F_D(\frac{t}{\alpha})\overline{F_{U}(t)}, &
\quad n=1, 2,\ldots
\end{cases}
\end{align}
\begin{align}
P\bigl\{A_n|S \approx t, G^1\bigr\} &=
\begin{cases}
\overline{F_X(t)}, & \quad n=0 \\
F_X(t)\left(F_{U}(t) F_{D}(\frac{t}{\alpha})\right)^{n-1}F_D(\frac{t}{\alpha})\overline{F_{U}(t)}, &
\quad n=1, 2,\ldots
\end{cases}
\end{align} \begin{align}
P\left\{E_n|S \approx t, G^1\right\} &= F_X(t)\left(F_{U}(t) F_{D}(\frac{t}{\alpha})\right)^n \overline{F_{D}(\frac{t}{\alpha})}, \quad \quad \quad \quad \quad \;\; n=0, 1, 2,\ldots.
\end{align}
\begin{align}
P\left\{E_n|S \approx t, G^1\right\} &= F_X(t)\left(F_{U}(t) F_{D}(\frac{t}{\alpha})\right)^n \overline{F_{D}(\frac{t}{\alpha})}, \quad \quad \quad \quad \quad \;\; n=0, 1, 2,\ldots.
\end{align}Then, we have that the conditional Laplace–Stieltjes transform of the completion time for A 0, under events G 1 and S = t as
and for An as
 \begin{align*}
E[e^{-sT} \mathbf{1}\{A_n\}|S \approx t,G^{1}] & = E\bigl[e^{-sT}|S=t,G^{1},A_{n}\bigr]P\{A_{n}|G^{1},S=t\} \notag \\
& = E\left[e^{-s\left(X+\sum_{i=2}^{n}U_{i} + \sum_{i=1}^n D_i + t\right)}|S=t,G^{1},A_{n}\right]F_X(t)\left(F_{U}(t) F_{D}(\frac{t}{\alpha})\right)^{n-1}\nonumber\\ &\quad\times F_D(\frac{t}{\alpha})\overline{F_{U}(t)}\notag\\
& = e^{-st} F_X(t)L_X(s|t)\bigl(F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})\bigr)^{n-1} \nonumber\\
&\quad \times F_D(\frac{t}{\alpha})L_D(s|\frac{t}{\alpha}) \overline{F_{U}(t)}, \forall n= 1, 2, \ldots.
\end{align*}
\begin{align*}
E[e^{-sT} \mathbf{1}\{A_n\}|S \approx t,G^{1}] & = E\bigl[e^{-sT}|S=t,G^{1},A_{n}\bigr]P\{A_{n}|G^{1},S=t\} \notag \\
& = E\left[e^{-s\left(X+\sum_{i=2}^{n}U_{i} + \sum_{i=1}^n D_i + t\right)}|S=t,G^{1},A_{n}\right]F_X(t)\left(F_{U}(t) F_{D}(\frac{t}{\alpha})\right)^{n-1}\nonumber\\ &\quad\times F_D(\frac{t}{\alpha})\overline{F_{U}(t)}\notag\\
& = e^{-st} F_X(t)L_X(s|t)\bigl(F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})\bigr)^{n-1} \nonumber\\
&\quad \times F_D(\frac{t}{\alpha})L_D(s|\frac{t}{\alpha}) \overline{F_{U}(t)}, \forall n= 1, 2, \ldots.
\end{align*} For the union of events An, ![]() $n = 0,1,2,\ldots$,
$n = 0,1,2,\ldots$,
 \begin{align}
E\left[e^{-sT}\mathbf{1}\{\cup_{n=0}^{\infty} A_{n}\}|S \approx t,G^{1}\right]
& = e^{-st} \Bigl[ \overline{F_X(t)} + \dfrac{F_X(t)L_X(s|t)F_D(\frac{t}{\alpha})L_D(s|\frac{t}{\alpha})\overline{F_{U}(t)}}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})}\Bigr].
\end{align}
\begin{align}
E\left[e^{-sT}\mathbf{1}\{\cup_{n=0}^{\infty} A_{n}\}|S \approx t,G^{1}\right]
& = e^{-st} \Bigl[ \overline{F_X(t)} + \dfrac{F_X(t)L_X(s|t)F_D(\frac{t}{\alpha})L_D(s|\frac{t}{\alpha})\overline{F_{U}(t)}}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})}\Bigr].
\end{align}Similarly,
 \begin{equation*}
E[e^{-sT} \mathbf{1}\{E_n\}|S \approx t,G^{1}]
= e^{-s\frac{t}{\alpha}} F_X(t)L_X(s|t) \bigl(F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})\bigr)^n
\overline{F_{D}(t/\alpha)}
\end{equation*}
\begin{equation*}
E[e^{-sT} \mathbf{1}\{E_n\}|S \approx t,G^{1}]
= e^{-s\frac{t}{\alpha}} F_X(t)L_X(s|t) \bigl(F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})\bigr)^n
\overline{F_{D}(t/\alpha)}
\end{equation*}and
 \begin{equation}
E\left[e^{-sT}\mathbf{1}\{\cup_{n=0}^{\infty} E_{n}\}|S \approx t,G^{1}\right]
= \dfrac{e^{-st/\alpha} F_{X}(t)L_{X}(s|t)\overline{F_{D}(\frac{t}{\alpha})}}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})}.
\end{equation}
\begin{equation}
E\left[e^{-sT}\mathbf{1}\{\cup_{n=0}^{\infty} E_{n}\}|S \approx t,G^{1}\right]
= \dfrac{e^{-st/\alpha} F_{X}(t)L_{X}(s|t)\overline{F_{D}(\frac{t}{\alpha})}}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})}.
\end{equation}Summing up (B.3) and (B.4), we obtain the conditional Laplace–Stieltjes transform of the completion time for customers arriving during an up period:
 \begin{equation}
L_{T}\left(s|S \approx t,G^{1}\right)
= e^{-st}\overline{F_{X}(t)} + \dfrac{F_{X}(t)L_{X}(s|t) \bigl(e^{-st} F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha}) \overline{F_{U}(t)} + e^{-s\frac{t}{\alpha}} \overline{F_{D}(\frac{t}{\alpha})}\bigr)}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})}.
\end{equation}
\begin{equation}
L_{T}\left(s|S \approx t,G^{1}\right)
= e^{-st}\overline{F_{X}(t)} + \dfrac{F_{X}(t)L_{X}(s|t) \bigl(e^{-st} F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha}) \overline{F_{U}(t)} + e^{-s\frac{t}{\alpha}} \overline{F_{D}(\frac{t}{\alpha})}\bigr)}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})}.
\end{equation} For work starting during a down period, we use the interpretation of events An, En, ![]() $n=0,1,\ldots$, as in the proof of Proposition 1 under G 2. The conditional completion time from Eq. (A.11) becomes
$n=0,1,\ldots$, as in the proof of Proposition 1 under G 2. The conditional completion time from Eq. (A.11) becomes
 \begin{equation}
\{T| S \approx t, G^2\} =
\begin{cases}
\frac{t}{\alpha}, & \quad \mbox{event }A_0,\\
Y+ \sum_{i=2}^{n}D_i + \sum_{i=1}^{n}U_i + \frac{t}{\alpha}, & \quad \mbox{event }A_n, \quad n = 0,1,2,\ldots\\
Y+ \sum_{i=2}^{n+1}D_i + \sum_{i=1}^{n}U_i + t, & \quad \mbox{event }E_n, \quad n = 0,1,2,\ldots
\end{cases}
\end{equation}
\begin{equation}
\{T| S \approx t, G^2\} =
\begin{cases}
\frac{t}{\alpha}, & \quad \mbox{event }A_0,\\
Y+ \sum_{i=2}^{n}D_i + \sum_{i=1}^{n}U_i + \frac{t}{\alpha}, & \quad \mbox{event }A_n, \quad n = 0,1,2,\ldots\\
Y+ \sum_{i=2}^{n+1}D_i + \sum_{i=1}^{n}U_i + t, & \quad \mbox{event }E_n, \quad n = 0,1,2,\ldots
\end{cases}
\end{equation}with probabilities,
 \begin{align}
P\bigl\{A_0|S \approx t, G^2\bigr\} &= \overline{F_{Y}(\frac{t}{\alpha})},
\end{align}
\begin{align}
P\bigl\{A_0|S \approx t, G^2\bigr\} &= \overline{F_{Y}(\frac{t}{\alpha})},
\end{align} \begin{align}
P\bigl\{A_n|S \approx t, G^2\bigr\} &= \bigl(F_{U}(t) F_{D}(\frac{t}{\alpha})\bigr)^{(n-1)} F_{Y}(\frac{t}{\alpha}) F_{U}(t) \overline{F_{D}(\frac{t}{\alpha})}, &n=1, 2, \ldots
\end{align}
\begin{align}
P\bigl\{A_n|S \approx t, G^2\bigr\} &= \bigl(F_{U}(t) F_{D}(\frac{t}{\alpha})\bigr)^{(n-1)} F_{Y}(\frac{t}{\alpha}) F_{U}(t) \overline{F_{D}(\frac{t}{\alpha})}, &n=1, 2, \ldots
\end{align} \begin{align}
P\{E_n|S \approx t, G^2\bigr\} &= \bigl(F_{U}(t) F_{D}(\frac{t}{\alpha})\bigr)^n F_{Y}(\frac{t}{\alpha})\overline{F_{U}(t)}, & n=0, 1, \ldots.
\end{align}
\begin{align}
P\{E_n|S \approx t, G^2\bigr\} &= \bigl(F_{U}(t) F_{D}(\frac{t}{\alpha})\bigr)^n F_{Y}(\frac{t}{\alpha})\overline{F_{U}(t)}, & n=0, 1, \ldots.
\end{align}From here,
 \begin{align*}
& E[e^{-sT} \mathbf{1}\{A_n\}|S \approx t,G^{2}] \nonumber\\
& =
\begin{cases}
e^{-st/\alpha}\overline{F_{Y}(\frac{t}{\alpha})}, & \quad n=0,\\
e^{-st/\alpha} \bigl(F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})\bigr)^{n-1} F_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha})F_{U}(t)L_{U}(s|t) \overline{F_{D}(\frac{t}{\alpha})}, & \quad n = 1,2,\ldots
\end{cases}
\end{align*}
\begin{align*}
& E[e^{-sT} \mathbf{1}\{A_n\}|S \approx t,G^{2}] \nonumber\\
& =
\begin{cases}
e^{-st/\alpha}\overline{F_{Y}(\frac{t}{\alpha})}, & \quad n=0,\\
e^{-st/\alpha} \bigl(F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})\bigr)^{n-1} F_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha})F_{U}(t)L_{U}(s|t) \overline{F_{D}(\frac{t}{\alpha})}, & \quad n = 1,2,\ldots
\end{cases}
\end{align*}and
 \begin{equation*}
E[e^{-sT} \mathbf{1}\{E_n\}|S \approx t,G^{2}]
= e^{-st} \bigl(F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})\bigr)^n
F_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha})\overline{F_{U}(t)}, \quad n = 0,1,2,\ldots.
\end{equation*}
\begin{equation*}
E[e^{-sT} \mathbf{1}\{E_n\}|S \approx t,G^{2}]
= e^{-st} \bigl(F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})\bigr)^n
F_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha})\overline{F_{U}(t)}, \quad n = 0,1,2,\ldots.
\end{equation*}Taking the union of events,
 \begin{equation*}
E\left[e^{-sT}\mathbf{1}\{\cup_{n=0}^{\infty} A_{n}\}|S \approx t,G^{2}\right]
= e^{-s\frac{t}{\alpha}} \left[ \overline{F_{Y}(\frac{t}{\alpha})} + \dfrac{F_{Y}(\frac{t}{\alpha})L_{Y}(s|\frac{t}{\alpha}) F_{U}(t) L_{U}(s|t) \overline{F_{D}(\frac{t}{\alpha})}}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})}\right]
\end{equation*}
\begin{equation*}
E\left[e^{-sT}\mathbf{1}\{\cup_{n=0}^{\infty} A_{n}\}|S \approx t,G^{2}\right]
= e^{-s\frac{t}{\alpha}} \left[ \overline{F_{Y}(\frac{t}{\alpha})} + \dfrac{F_{Y}(\frac{t}{\alpha})L_{Y}(s|\frac{t}{\alpha}) F_{U}(t) L_{U}(s|t) \overline{F_{D}(\frac{t}{\alpha})}}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})}\right]
\end{equation*}and
 \begin{equation*}
E\left[e^{-sT}\mathbf{1}\{\cup_{n=0}^{\infty} E_{n}\}|S \approx t,G^{2}\right]
= \dfrac{e^{-st} F_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha})\overline{F_{U}(t)}}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})},
\end{equation*}
\begin{equation*}
E\left[e^{-sT}\mathbf{1}\{\cup_{n=0}^{\infty} E_{n}\}|S \approx t,G^{2}\right]
= \dfrac{e^{-st} F_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha})\overline{F_{U}(t)}}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})},
\end{equation*}and combining all events under G 2,
 \begin{equation}
L_{T}\left(s|S \approx t,G^{2}\right)
= e^{-st\frac{t}{\alpha}}\overline{F_{Y}(\frac{t}{\alpha})} + \dfrac{F_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha})\bigl( e^{-st}\overline{F_{U}(t)} +e^{-s\frac{t}{\alpha}}F_{U}(t) L_{U}(s|t)\overline{F_{D}(\frac{t}{\alpha})} \bigr)}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})}.
\end{equation}
\begin{equation}
L_{T}\left(s|S \approx t,G^{2}\right)
= e^{-st\frac{t}{\alpha}}\overline{F_{Y}(\frac{t}{\alpha})} + \dfrac{F_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha})\bigl( e^{-st}\overline{F_{U}(t)} +e^{-s\frac{t}{\alpha}}F_{U}(t) L_{U}(s|t)\overline{F_{D}(\frac{t}{\alpha})} \bigr)}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})}.
\end{equation}Finally combining Laplace–Stieltjes transform for events G 1 and G 2 from (B.5) and (B.10), and considering the probabilities in (2.1), we obtain
 \begin{align*}
L_{T}\left(s|S \approx t\right)
= & \phantom{\,+\,}
\dfrac{r}{(r+f)} \bigl[e^{-st}\overline{F_{X}(t)} + \dfrac{F_{X}(t)L_{X}(s|t) \bigl(e^{-st} F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha}) \overline{F_{U}(t)} + e^{-st/\alpha} \overline{F_{D}(\frac{t}{\alpha})}\bigr)}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})} \bigr]\\
& +
\dfrac{f}{(r+f)}\bigl[e^{-s\frac{t}{\alpha}}\overline{F_{Y}(\frac{t}{\alpha})} +
\dfrac{F_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha})\bigl( e^{-st}\overline{F_{U}(t)} +e^{-s\frac{t}{\alpha}}F_{U}(t) L_{U}(s|t)\overline{F_{D}(\frac{t}{\alpha})} \bigr)}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})}\bigr],
\end{align*}
\begin{align*}
L_{T}\left(s|S \approx t\right)
= & \phantom{\,+\,}
\dfrac{r}{(r+f)} \bigl[e^{-st}\overline{F_{X}(t)} + \dfrac{F_{X}(t)L_{X}(s|t) \bigl(e^{-st} F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha}) \overline{F_{U}(t)} + e^{-st/\alpha} \overline{F_{D}(\frac{t}{\alpha})}\bigr)}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})} \bigr]\\
& +
\dfrac{f}{(r+f)}\bigl[e^{-s\frac{t}{\alpha}}\overline{F_{Y}(\frac{t}{\alpha})} +
\dfrac{F_{Y}(\frac{t}{\alpha}) L_{Y}(s|\frac{t}{\alpha})\bigl( e^{-st}\overline{F_{U}(t)} +e^{-s\frac{t}{\alpha}}F_{U}(t) L_{U}(s|t)\overline{F_{D}(\frac{t}{\alpha})} \bigr)}
{1-F_{U}(t)L_{U}(s|t) F_{D}(\frac{t}{\alpha})L_{D}(s|\frac{t}{\alpha})}\bigr],
\end{align*}gives the result in Eq. (2.23).
Appendix C. Proof of Theorem 2.8
As in Theorem 2.5, we condition the service time to a task length S = t. Recalling the events in Eq. (2.21), and the probabilities in Eqs. (B.1)–(B.2), it can be shown that
 \begin{align*}
&E[T\cdot\mathbf{1}\{A_n\} | S \approx t, G^1]
= E[T|A_n,S \approx t,G^1]P\{A_{n}|G^{1}\} \\
&\quad = \begin{cases}
t \overline{F_{X}(t)}, & n=0\\
\bigl[t + E[X|t] + E[D|\frac{t}{\alpha}] + (n-1) \bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr) \bigr] F_{X}(t) \bigl(F_{U}(t) F_{D}(\frac{t}{\alpha})\bigr)^{n-1}F_{D}(\frac{t}{\alpha})\overline{F_{U}(t)}, & n=1, 2, \ldots
\end{cases}\\
&E[T\cdot\mathbf{1}\{E_n\} | S \approx t,G^1]
= \bigl[\frac{t}{\alpha} +E[X|t] + n\bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr) \bigr] F_{X}(t) \bigl(F_{U}(t)F_{D}(\frac{t}{\alpha})\bigr)^{n} \overline{F_{D}(\frac{t}{\alpha})}, \quad \quad \quad \quad n= 0, 1,2,\ldots.
\end{align*}
\begin{align*}
&E[T\cdot\mathbf{1}\{A_n\} | S \approx t, G^1]
= E[T|A_n,S \approx t,G^1]P\{A_{n}|G^{1}\} \\
&\quad = \begin{cases}
t \overline{F_{X}(t)}, & n=0\\
\bigl[t + E[X|t] + E[D|\frac{t}{\alpha}] + (n-1) \bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr) \bigr] F_{X}(t) \bigl(F_{U}(t) F_{D}(\frac{t}{\alpha})\bigr)^{n-1}F_{D}(\frac{t}{\alpha})\overline{F_{U}(t)}, & n=1, 2, \ldots
\end{cases}\\
&E[T\cdot\mathbf{1}\{E_n\} | S \approx t,G^1]
= \bigl[\frac{t}{\alpha} +E[X|t] + n\bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr) \bigr] F_{X}(t) \bigl(F_{U}(t)F_{D}(\frac{t}{\alpha})\bigr)^{n} \overline{F_{D}(\frac{t}{\alpha})}, \quad \quad \quad \quad n= 0, 1,2,\ldots.
\end{align*}From here,
 \begin{align}
E[T\cdot\mathbf{1}\{\cup_{i=0}^{\infty}A_n\} | S \approx t,G^1]
&= \dfrac{\bigl[t + E[X|t] + E[D|\frac{t}{\alpha}]\bigr] F_{X}(t) F_{D}(\frac{t}{\alpha})\overline{F_{U}(t)}}{1-F_{U}(t)F_{D}(\frac{t}{\alpha})} \nonumber\\
&\quad + \dfrac{\bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr)F_{X}(t) F_{U}(t) \bigl(F_{D}(\frac{t}{\alpha})\bigr)^2\overline{F_{U}(t)}}
{(1-F_{U}(t)F_{D}(\frac{t}{\alpha}))^{2}},
\end{align}
\begin{align}
E[T\cdot\mathbf{1}\{\cup_{i=0}^{\infty}A_n\} | S \approx t,G^1]
&= \dfrac{\bigl[t + E[X|t] + E[D|\frac{t}{\alpha}]\bigr] F_{X}(t) F_{D}(\frac{t}{\alpha})\overline{F_{U}(t)}}{1-F_{U}(t)F_{D}(\frac{t}{\alpha})} \nonumber\\
&\quad + \dfrac{\bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr)F_{X}(t) F_{U}(t) \bigl(F_{D}(\frac{t}{\alpha})\bigr)^2\overline{F_{U}(t)}}
{(1-F_{U}(t)F_{D}(\frac{t}{\alpha}))^{2}},
\end{align} \begin{align}
E[T\cdot\mathbf{1}\{\cup_{i=0}^{\infty}E_n\} | S \approx t,G^1]
&= \dfrac{\bigl(\frac{t}{\alpha} + E[X|t]\bigr)F_{X}(t)\overline{F_{D}(\frac{t}{\alpha})}}{1-F_{U}(t)F_{D}(\frac{t}{\alpha})} \nonumber\\
&\quad + \dfrac{\bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr)F_{X}(t) F_{D}(\frac{t}{\alpha})F_{U}(t)\overline{F_{D}(\frac{t}{\alpha})}}{(1-F_{U}(t)F_{D}(\frac{t}{\alpha}))^2}.
\end{align}
\begin{align}
E[T\cdot\mathbf{1}\{\cup_{i=0}^{\infty}E_n\} | S \approx t,G^1]
&= \dfrac{\bigl(\frac{t}{\alpha} + E[X|t]\bigr)F_{X}(t)\overline{F_{D}(\frac{t}{\alpha})}}{1-F_{U}(t)F_{D}(\frac{t}{\alpha})} \nonumber\\
&\quad + \dfrac{\bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr)F_{X}(t) F_{D}(\frac{t}{\alpha})F_{U}(t)\overline{F_{D}(\frac{t}{\alpha})}}{(1-F_{U}(t)F_{D}(\frac{t}{\alpha}))^2}.
\end{align}Summing up (C.1) and (C.2) and simplifying we obtain
 \begin{align}
E[T|S \approx t,G^{1}] &= t \overline{F_{X}(t)} + F_X(t)\Bigl[E[X|t] \nonumber\\
&\quad + \dfrac{\bigl(tF_{D}(\frac{t}{\alpha})\overline{F_{U}(t)}+\frac{t}{\alpha}\overline{F_{D}(\frac{t}{\alpha})}\bigr)
+ F_{D}(\frac{t}{\alpha})\bigl(E[U|t]F_U(t)+E[D|\frac{t}{\alpha}]\bigr)}{1-F_{U}(t)F_{D}(\frac{t}{\alpha})}\Bigr].
\end{align}
\begin{align}
E[T|S \approx t,G^{1}] &= t \overline{F_{X}(t)} + F_X(t)\Bigl[E[X|t] \nonumber\\
&\quad + \dfrac{\bigl(tF_{D}(\frac{t}{\alpha})\overline{F_{U}(t)}+\frac{t}{\alpha}\overline{F_{D}(\frac{t}{\alpha})}\bigr)
+ F_{D}(\frac{t}{\alpha})\bigl(E[U|t]F_U(t)+E[D|\frac{t}{\alpha}]\bigr)}{1-F_{U}(t)F_{D}(\frac{t}{\alpha})}\Bigr].
\end{align}Consider now the events from Eq. (2.22), and the probabilities in (B.8)–(B.9). Then it holds that
 \begin{align*}
E[T\cdot\mathbf{1}\{A_0\} | S \approx t,G^2]
& = \frac{t}{\alpha} \overline{F_{Y}(\frac{t}{\alpha})},\\
E[T\cdot\mathbf{1}\{A_n\} | S \approx t,G^2]
&= \bigl[\frac{t}{\alpha} + E[Y|\frac{t}{\alpha}]+ (n-1)\bigl(E[U|U \lt t]+E[D|\frac{t}{\alpha}]\bigr) \nonumber\\
&\quad + E[U|t]\bigr] F_Y(\frac{t}{\alpha}) F_U(t)
\bigl(F_{U}(t)F_{D}(\frac{t}{\alpha})\bigr)^{n-1}
\overline{F_{D}(\frac{t}{\alpha})}, \\
E[T\cdot\mathbf{1}\{E_n\} | S \approx t,G^2]
&= \bigl[t + E[Y|\frac{t}{\alpha}]+n \bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr)\bigr] F_Y(\frac{t}{\alpha}) \bigl(F_{U}(t)F_{D}(\frac{t}{\alpha})\bigr)^{n}\overline{F_{U}(t)}.
\end{align*}
\begin{align*}
E[T\cdot\mathbf{1}\{A_0\} | S \approx t,G^2]
& = \frac{t}{\alpha} \overline{F_{Y}(\frac{t}{\alpha})},\\
E[T\cdot\mathbf{1}\{A_n\} | S \approx t,G^2]
&= \bigl[\frac{t}{\alpha} + E[Y|\frac{t}{\alpha}]+ (n-1)\bigl(E[U|U \lt t]+E[D|\frac{t}{\alpha}]\bigr) \nonumber\\
&\quad + E[U|t]\bigr] F_Y(\frac{t}{\alpha}) F_U(t)
\bigl(F_{U}(t)F_{D}(\frac{t}{\alpha})\bigr)^{n-1}
\overline{F_{D}(\frac{t}{\alpha})}, \\
E[T\cdot\mathbf{1}\{E_n\} | S \approx t,G^2]
&= \bigl[t + E[Y|\frac{t}{\alpha}]+n \bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr)\bigr] F_Y(\frac{t}{\alpha}) \bigl(F_{U}(t)F_{D}(\frac{t}{\alpha})\bigr)^{n}\overline{F_{U}(t)}.
\end{align*}Taking the union of events, we get
 \begin{align}
E[T\cdot\mathbf{1}\{\cup_{i=0}^{\infty}A_n\} | S \approx t,G^2]
&= \frac{t}{\alpha} \overline{F_Y(\frac{t}{\alpha})} + \dfrac{\frac{t}{\alpha} F_Y(\frac{t}{\alpha}) F_U(t)\overline{F_{D}(\frac{t}{\alpha})} }{1-F_{U}(t)F_{D}(\frac{t}{\alpha})} \nonumber\\
&\quad + \dfrac{\bigl(E[Y|\frac{t}{\alpha}] + E[U|t]\bigr) F_{D}(\frac{t}{\alpha})F_{U}(t) \overline{F_{D}(\frac{t}{\alpha})}}
{(1-F_{U}(t)F_{D}(\frac{t}{\alpha}))} \notag\\
& \quad + \dfrac{\bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr) F_Y(\frac{t}{\alpha}) (F_{U}(t))^2 F_{D}(\frac{t}{\alpha})\overline{F_{D}(\frac{t}{\alpha})}}
{(1-F_{U}(t)F_{D}(\frac{t}{\alpha}))^{2}},
\end{align}
\begin{align}
E[T\cdot\mathbf{1}\{\cup_{i=0}^{\infty}A_n\} | S \approx t,G^2]
&= \frac{t}{\alpha} \overline{F_Y(\frac{t}{\alpha})} + \dfrac{\frac{t}{\alpha} F_Y(\frac{t}{\alpha}) F_U(t)\overline{F_{D}(\frac{t}{\alpha})} }{1-F_{U}(t)F_{D}(\frac{t}{\alpha})} \nonumber\\
&\quad + \dfrac{\bigl(E[Y|\frac{t}{\alpha}] + E[U|t]\bigr) F_{D}(\frac{t}{\alpha})F_{U}(t) \overline{F_{D}(\frac{t}{\alpha})}}
{(1-F_{U}(t)F_{D}(\frac{t}{\alpha}))} \notag\\
& \quad + \dfrac{\bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr) F_Y(\frac{t}{\alpha}) (F_{U}(t))^2 F_{D}(\frac{t}{\alpha})\overline{F_{D}(\frac{t}{\alpha})}}
{(1-F_{U}(t)F_{D}(\frac{t}{\alpha}))^{2}},
\end{align} \begin{align}
E[T\cdot\mathbf{1}\{\cup_{i=0}^{\infty}E_n\} | S \approx t,G^2]
&= \dfrac{\bigl(t+E[Y|\frac{t}{\alpha}]\bigr)F_Y(\frac{t}{\alpha}) \overline{F_{U}(t)}}{1-F_{U}(t)F_{D}(\frac{t}{\alpha})} \nonumber\\
&\quad + \dfrac{\bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr)F_Y(\frac{t}{\alpha}) F_{U}(t)F_{D}(\frac{t}{\alpha})\overline{F_{U}(t)}}
{(1-F_{U}(t)F_{D}(\frac{t}{\alpha}))^{2}}
\end{align}
\begin{align}
E[T\cdot\mathbf{1}\{\cup_{i=0}^{\infty}E_n\} | S \approx t,G^2]
&= \dfrac{\bigl(t+E[Y|\frac{t}{\alpha}]\bigr)F_Y(\frac{t}{\alpha}) \overline{F_{U}(t)}}{1-F_{U}(t)F_{D}(\frac{t}{\alpha})} \nonumber\\
&\quad + \dfrac{\bigl(E[U|t]+E[D|\frac{t}{\alpha}]\bigr)F_Y(\frac{t}{\alpha}) F_{U}(t)F_{D}(\frac{t}{\alpha})\overline{F_{U}(t)}}
{(1-F_{U}(t)F_{D}(\frac{t}{\alpha}))^{2}}
\end{align}and summing up (C.4) and (C.5) we obtain,
 \begin{align}
E[T|S \approx t,G^{2}] = & \phantom{+ } \frac{t}{\alpha} \overline{F_Y(\frac{t}{\alpha}) } + F_Y(\frac{t}{\alpha}) \Bigl[E[Y|\frac{t}{\alpha}] \nonumber\\
&\quad + \dfrac{
\bigl(\frac{t}{\alpha}F_U(t)\overline{F_{D}(\frac{t}{\alpha})} + t\overline{F_{U}(t)}\bigr) +F_{U}(t) \bigl(E[U|t] + E[D|\frac{t}{\alpha}]F_{D}(\frac{t}{\alpha})\bigr) }{1-F_{U}(t)F_{D}(\frac{t}{\alpha})}\Bigr].
\end{align}
\begin{align}
E[T|S \approx t,G^{2}] = & \phantom{+ } \frac{t}{\alpha} \overline{F_Y(\frac{t}{\alpha}) } + F_Y(\frac{t}{\alpha}) \Bigl[E[Y|\frac{t}{\alpha}] \nonumber\\
&\quad + \dfrac{
\bigl(\frac{t}{\alpha}F_U(t)\overline{F_{D}(\frac{t}{\alpha})} + t\overline{F_{U}(t)}\bigr) +F_{U}(t) \bigl(E[U|t] + E[D|\frac{t}{\alpha}]F_{D}(\frac{t}{\alpha})\bigr) }{1-F_{U}(t)F_{D}(\frac{t}{\alpha})}\Bigr].
\end{align}Finally, combining (C.3) and (C.6) with the probabilities (2.1), we obtain the result in (2.25).
Appendix D. Proof of Theorem 3.1
Proof. As in Fiorini et al. [Reference Fiorini, Sheahan and Lipsky16], we calculate the moments of the completion time distribution to assess the heaviness of the tail. We assume here that the task size has an exponential tail, which amounts to ![]() $\theta_{\text{min}}(S) = \mu$ from Eq. (3.3), and denote
$\theta_{\text{min}}(S) = \mu$ from Eq. (3.3), and denote ![]() $\Delta = \min\{f,r/\alpha\} \gt 0$ and
$\Delta = \min\{f,r/\alpha\} \gt 0$ and ![]() $\Delta^{+} = f + r/\alpha - \Delta = \max\{f,r/\alpha\} \gt 0$. Let U and D be exponentially distributed with failure rate f and repair rate r, respectively. Their distributions are
$\Delta^{+} = f + r/\alpha - \Delta = \max\{f,r/\alpha\} \gt 0$. Let U and D be exponentially distributed with failure rate f and repair rate r, respectively. Their distributions are ![]() $F_{U}(t) = 1-e^{-ft}$, and
$F_{U}(t) = 1-e^{-ft}$, and ![]() $F_{D}(t) = 1-e^{-rt}$.
$F_{D}(t) = 1-e^{-rt}$.
Notice that the task-size-conditioned Laplace–Stieltjes transform can be expressed as in (D.1)–(D.2)
 \begin{align}
L_{U}(s|t) & = E[e^{-sU}|t \gt U]
= \int_{x=0}^{t}e^{-sx}dF_{U}(x|t)
= \int_{x=0}^{t}e^{-sx}\dfrac{fe^{-fx}}{F_{U}(t)}dx
= \dfrac{f}{s+f}\dfrac{1-e^{-(s+f)t}}{1-e^{-ft}},
\end{align}
\begin{align}
L_{U}(s|t) & = E[e^{-sU}|t \gt U]
= \int_{x=0}^{t}e^{-sx}dF_{U}(x|t)
= \int_{x=0}^{t}e^{-sx}\dfrac{fe^{-fx}}{F_{U}(t)}dx
= \dfrac{f}{s+f}\dfrac{1-e^{-(s+f)t}}{1-e^{-ft}},
\end{align} \begin{align}
L_{D}(s|t/\alpha) & = E[e^{-sD}|t \gt D]
= \int_{x=0}^{t/\alpha}e^{-sx}dF_{D}(x|t/\alpha)
= \int_{x=0}^{t/\alpha}e^{-sx}\dfrac{re^{-rx}}{F_{D}(t/\alpha)}dx
= \dfrac{r}{s+r}\dfrac{1-e^{-(s+r)t/\alpha}}{1-e^{-rt/\alpha}}.
\end{align}
\begin{align}
L_{D}(s|t/\alpha) & = E[e^{-sD}|t \gt D]
= \int_{x=0}^{t/\alpha}e^{-sx}dF_{D}(x|t/\alpha)
= \int_{x=0}^{t/\alpha}e^{-sx}\dfrac{re^{-rx}}{F_{D}(t/\alpha)}dx
= \dfrac{r}{s+r}\dfrac{1-e^{-(s+r)t/\alpha}}{1-e^{-rt/\alpha}}.
\end{align}From Theorem 2.5, the conditional Laplace–Stieltjes transform of the completion time in Eq. (2.23) becomes
 \begin{equation*}
L_{T}(s|t) =
\dfrac{
re^{-(s+f)t}
\left[1 + \dfrac{f}{s+r}(1-e^{-(s+r)t/\alpha})\right]
+
fe^{-(s+r)t/\alpha}
\left[1 + \dfrac{r}{s+f}(1-e^{-(s+f)t})\right]
}{
(r+f)
\left[
1-
\dfrac{rf}{(s+r)(s+f)}
(1-e^{-(s+f)t})
(1-e^{-(s+r)t/\alpha})
\right]
},
\end{equation*}
\begin{equation*}
L_{T}(s|t) =
\dfrac{
re^{-(s+f)t}
\left[1 + \dfrac{f}{s+r}(1-e^{-(s+r)t/\alpha})\right]
+
fe^{-(s+r)t/\alpha}
\left[1 + \dfrac{r}{s+f}(1-e^{-(s+f)t})\right]
}{
(r+f)
\left[
1-
\dfrac{rf}{(s+r)(s+f)}
(1-e^{-(s+f)t})
(1-e^{-(s+r)t/\alpha})
\right]
},
\end{equation*}where we call
 \begin{align*}
h_{r}(s,t) & := \dfrac{f}{s+r}(1-e^{-(s+r)t/\alpha}), \\
h_{f}(s,t) & := \dfrac{r}{s+f}(1-e^{-(s+f)t}),
\end{align*}
\begin{align*}
h_{r}(s,t) & := \dfrac{f}{s+r}(1-e^{-(s+r)t/\alpha}), \\
h_{f}(s,t) & := \dfrac{r}{s+f}(1-e^{-(s+f)t}),
\end{align*}obtaining
 \begin{equation}
L_{T}(s|t) =
\dfrac{1}{r+f}\cdot
\dfrac{
re^{-(s+f)t}(1 + h_{r}(s,t))
+
fe^{-(s+r)t/\alpha}(1 + h_{f}(s,t))
}{1-h_{r}(s,t)h_{f}(s,t)}.
\end{equation}
\begin{equation}
L_{T}(s|t) =
\dfrac{1}{r+f}\cdot
\dfrac{
re^{-(s+f)t}(1 + h_{r}(s,t))
+
fe^{-(s+r)t/\alpha}(1 + h_{f}(s,t))
}{1-h_{r}(s,t)h_{f}(s,t)}.
\end{equation} To calculate the mth moment ![]() $E[T^{m}]$ of the completion time T, we resort to the derivatives of the Laplace–Stieltjes transform of the completion time distribution evaluated at s = 0 as shown in Eq. (D.4)
$E[T^{m}]$ of the completion time T, we resort to the derivatives of the Laplace–Stieltjes transform of the completion time distribution evaluated at s = 0 as shown in Eq. (D.4)
 \begin{equation}
E[T^{m}] = \left.(-1)^{m}\dfrac{d^{m}}{ds^{m}}L_{T}(s)\right|_{s=0}.
\end{equation}
\begin{equation}
E[T^{m}] = \left.(-1)^{m}\dfrac{d^{m}}{ds^{m}}L_{T}(s)\right|_{s=0}.
\end{equation}In particular, however, we calculate the mth partial derivative with respect to s of the conditioned Laplace–Stieltjes transform for the completion time in (D.3), evaluate at s = 0, and uncondition with respect to the task size whenever is possible.
Consider the following function definitions and notation for the partial derivatives of the conditional Laplace Stieljest Transform (LSTm):
(1) Main term for the nth derivative:
 \begin{equation*}
L_{T}(s;n|t) :=
\dfrac{1}{r+f}\cdot
\dfrac{
re^{-(s+f)t}(1 + h_{r}(s,t))
+
\frac{f}{\alpha^{n}}e^{-(s+r)t/\alpha}(1 + h_{f}(s,t))
}{1-h_{r}(s,t)h_{f}(s,t)}, \quad n = 0,1,2,\ldots.
\end{equation*}
\begin{equation*}
L_{T}(s;n|t) :=
\dfrac{1}{r+f}\cdot
\dfrac{
re^{-(s+f)t}(1 + h_{r}(s,t))
+
\frac{f}{\alpha^{n}}e^{-(s+r)t/\alpha}(1 + h_{f}(s,t))
}{1-h_{r}(s,t)h_{f}(s,t)}, \quad n = 0,1,2,\ldots.
\end{equation*}Notice
 $L_{T}(s;0|t) := L_{T}(s|t)$.
$L_{T}(s;0|t) := L_{T}(s|t)$.(2) First recurrent factor of higher-order term for nth derivative:
(D.5) \begin{equation}
\nu_{n}(s,t) :=
\dfrac{re^{-(s+f)t} + \frac{f}{\alpha^{n-1}}e^{-(s+r)t/\alpha}}{r+f},
\quad n = 1,2,\ldots.
\end{equation}
\begin{equation}
\nu_{n}(s,t) :=
\dfrac{re^{-(s+f)t} + \frac{f}{\alpha^{n-1}}e^{-(s+r)t/\alpha}}{r+f},
\quad n = 1,2,\ldots.
\end{equation}It holds that
 $\frac{\partial^{n}}{\partial s^{n}}\nu_{1}(s,t) = (-1)^{n}t^{n}\nu_{n+1}(s,t)$.
$\frac{\partial^{n}}{\partial s^{n}}\nu_{1}(s,t) = (-1)^{n}t^{n}\nu_{n+1}(s,t)$.(3) Recurrent rational exponential functions and terms:
(D.6) \begin{equation}
\theta_i(s,t;a,b) := \dfrac{e^{-i(s+a)t/b}}{1-e^{-i(s+a)t/b}}.
\end{equation}
\begin{equation}
\theta_i(s,t;a,b) := \dfrac{e^{-i(s+a)t/b}}{1-e^{-i(s+a)t/b}}.
\end{equation}It can be shown that for
 $n\geq1$,
(D.7)
$n\geq1$,
(D.7) \begin{align}
\frac{\partial^{n}}{\partial s^{n}}\theta_1(s,t;a,b)
& \phantom{:}=
(-1)^{n}\left(\frac{t}{b}\right)^{\!\!n}
\sum_{i=1}^{n+1}W(n,i)\dfrac{e^{-i(s+a)t/b}}{(1-e^{-(s+a)t/b})^{i}} \notag \\
& := (-1)^{n}\left(\frac{t}{b}\right)^{\!\!n} \sum_{i=1}^{n+1}W(n,i)\theta_{i}(s,t;a,b),
\end{align}
\begin{align}
\frac{\partial^{n}}{\partial s^{n}}\theta_1(s,t;a,b)
& \phantom{:}=
(-1)^{n}\left(\frac{t}{b}\right)^{\!\!n}
\sum_{i=1}^{n+1}W(n,i)\dfrac{e^{-i(s+a)t/b}}{(1-e^{-(s+a)t/b})^{i}} \notag \\
& := (-1)^{n}\left(\frac{t}{b}\right)^{\!\!n} \sum_{i=1}^{n+1}W(n,i)\theta_{i}(s,t;a,b),
\end{align}where
 $W(n,i)$ denotes the nth row and ith column’s Worpitzky number from the Worpitzky triangle [Reference Sloane35], as defined in (D.8)
(D.8)
$W(n,i)$ denotes the nth row and ith column’s Worpitzky number from the Worpitzky triangle [Reference Sloane35], as defined in (D.8)
(D.8) \begin{equation}
W(n,i) = \dfrac{1}{i}\sum_{j=0}^{i} (-1)^{i-j}\binom{i}{j}j^{n},
\quad n \geq 1, \quad 1 \leq i \leq n.
\end{equation}
\begin{equation}
W(n,i) = \dfrac{1}{i}\sum_{j=0}^{i} (-1)^{i-j}\binom{i}{j}j^{n},
\quad n \geq 1, \quad 1 \leq i \leq n.
\end{equation}In order to simplify the formulas, we also give the following notation:
(D.9) \begin{align}
\Theta_1(s,t;a,b) & :=
\dfrac{t}{b}\cdot\dfrac{e^{-(s+a)t/b}}{1-e^{-(s+a)t/b}}-\dfrac{1}{s+a} \notag \\
& \phantom{:}= \dfrac{t}{b}\theta_1(s,t;a,b)-\dfrac{1}{s+a}.
\end{align}
\begin{align}
\Theta_1(s,t;a,b) & :=
\dfrac{t}{b}\cdot\dfrac{e^{-(s+a)t/b}}{1-e^{-(s+a)t/b}}-\dfrac{1}{s+a} \notag \\
& \phantom{:}= \dfrac{t}{b}\theta_1(s,t;a,b)-\dfrac{1}{s+a}.
\end{align}From here, similarly, for
 $n\geq0$,
(D.10)
$n\geq0$,
(D.10) \begin{align}
\frac{\partial^{n}}{\partial s^{n}}\Theta_1(s,t;a,b)
& \phantom{:}=
(-1)^{n}
\left(
\dfrac{t^{n+1}}{b^{n+1}}
\sum_{i=1}^{n+1}W(n,i)
\theta_{i}(s,t;a,b)
-\dfrac{n!}{(s+a)^{n+1}}
\right) \notag \\
& := \Theta_{n+1}(s,t;a,b).
\end{align}
\begin{align}
\frac{\partial^{n}}{\partial s^{n}}\Theta_1(s,t;a,b)
& \phantom{:}=
(-1)^{n}
\left(
\dfrac{t^{n+1}}{b^{n+1}}
\sum_{i=1}^{n+1}W(n,i)
\theta_{i}(s,t;a,b)
-\dfrac{n!}{(s+a)^{n+1}}
\right) \notag \\
& := \Theta_{n+1}(s,t;a,b).
\end{align}Finally, we call
(D.11) \begin{equation}
\omega_{n}(s,t) := \Theta_{n}(s,t;f,1) + \Theta_{n}(s,t;r,\alpha), \quad n = 1,2,\ldots
\end{equation}
\begin{equation}
\omega_{n}(s,t) := \Theta_{n}(s,t;f,1) + \Theta_{n}(s,t;r,\alpha), \quad n = 1,2,\ldots
\end{equation}and by definition,
 $\frac{\partial^{n}}{\partial s^{n}}\omega_{1}(s,t) = \omega_{n+1}(s,t)$.
$\frac{\partial^{n}}{\partial s^{n}}\omega_{1}(s,t) = \omega_{n+1}(s,t)$.
Now we calculate de first derivative of the conditioned Laplace–Stieltjes transform in Eq. (D.3). Henceforth, functional dependencies of ![]() $h_{r}(s,t)$ and
$h_{r}(s,t)$ and ![]() $h_{f}(s,t)$ may be omitted for cleaner notation
$h_{f}(s,t)$ may be omitted for cleaner notation
 \begin{align}
\dfrac{\partial}{\partial s}L_{T}(s|t)
= & \phantom{- } \dfrac{\partial}{\partial s}L_{T}(s;0|t) \notag \\
= &
-tL_{T}(s;1|t)
+
\nu_{1}(s,t)
\dfrac{
\frac{\partial}{\partial s}
(h_{r}h_{f})
}{(1-h_{r}h_{f})^{2}} \notag \\
&
+
\dfrac{s+f}{r+f}
\theta_1(s,t;f,1)
\Bigl(\Theta_1(s,t;r,\alpha)+h_{r}h_{f}\Theta_1(s,t;f,1)\Bigr)
\dfrac{h_{r}h_{f}}{(1-h_{r}h_{f})^{2}} \notag \\
&
+
\dfrac{s+r}{r+f}
\theta_1(s,t;r,\alpha)
\Bigl(\Theta_1(s,t;f,1)+h_{r}h_{f}\Theta_1(s,t;r,\alpha)\Bigr)
\dfrac{h_{r}h_{f}}{\bigl(1-h_{r}h_{f}\bigr)^{2}} \notag \\
:= &
-tL_{T}(s;1|t)
+
\nu_{1}(s,t)
\dfrac{
\frac{\partial}{\partial s}
(h_{r}h_{f})
}{(1-h_{r}h_{f})^{2}} \notag \\
&
+
\left[
\dfrac{s+f}{r+f}
\theta_1(s,t;f,1)
A(s,t)
+
\dfrac{s+r}{r+f}
\theta_1(s,t;r,\alpha)
B(s,t)
\right]
\dfrac{h_{r}h_{f}}{(1-h_{r}h_{f})^{2}},
\end{align}
\begin{align}
\dfrac{\partial}{\partial s}L_{T}(s|t)
= & \phantom{- } \dfrac{\partial}{\partial s}L_{T}(s;0|t) \notag \\
= &
-tL_{T}(s;1|t)
+
\nu_{1}(s,t)
\dfrac{
\frac{\partial}{\partial s}
(h_{r}h_{f})
}{(1-h_{r}h_{f})^{2}} \notag \\
&
+
\dfrac{s+f}{r+f}
\theta_1(s,t;f,1)
\Bigl(\Theta_1(s,t;r,\alpha)+h_{r}h_{f}\Theta_1(s,t;f,1)\Bigr)
\dfrac{h_{r}h_{f}}{(1-h_{r}h_{f})^{2}} \notag \\
&
+
\dfrac{s+r}{r+f}
\theta_1(s,t;r,\alpha)
\Bigl(\Theta_1(s,t;f,1)+h_{r}h_{f}\Theta_1(s,t;r,\alpha)\Bigr)
\dfrac{h_{r}h_{f}}{\bigl(1-h_{r}h_{f}\bigr)^{2}} \notag \\
:= &
-tL_{T}(s;1|t)
+
\nu_{1}(s,t)
\dfrac{
\frac{\partial}{\partial s}
(h_{r}h_{f})
}{(1-h_{r}h_{f})^{2}} \notag \\
&
+
\left[
\dfrac{s+f}{r+f}
\theta_1(s,t;f,1)
A(s,t)
+
\dfrac{s+r}{r+f}
\theta_1(s,t;r,\alpha)
B(s,t)
\right]
\dfrac{h_{r}h_{f}}{(1-h_{r}h_{f})^{2}},
\end{align} with ![]() $A(s,t) = \Theta_1(s,t;r,\alpha)+h_{r}h_{f}\Theta_1(s,t;f,1)$ and
$A(s,t) = \Theta_1(s,t;r,\alpha)+h_{r}h_{f}\Theta_1(s,t;f,1)$ and ![]() $B(s,t) = \Theta_1(s,t;f,1)+h_{r}h_{f}\Theta_1(s,t;r,\alpha)$.
$B(s,t) = \Theta_1(s,t;f,1)+h_{r}h_{f}\Theta_1(s,t;r,\alpha)$.
It can be shown that
 \begin{equation}
\dfrac{\partial}{\partial s}(h_{r}h_{f})
= h_{r}h_{f}\omega_{1}(s,t).
\end{equation}
\begin{equation}
\dfrac{\partial}{\partial s}(h_{r}h_{f})
= h_{r}h_{f}\omega_{1}(s,t).
\end{equation}Then, calling
 \begin{equation}
u_1(s,t) := \dfrac{h_{r}h_{f}}{(1-h_{r}h_{f})^{2}},
\end{equation}
\begin{equation}
u_1(s,t) := \dfrac{h_{r}h_{f}}{(1-h_{r}h_{f})^{2}},
\end{equation}we have from (D.12),
 \begin{align}
\dfrac{\partial}{\partial s}L_{T}(s|t) & =
-tL_{T}(s;1|t) + u_1(s,t) \left[ \nu_{1}(s,t)\omega_{1}(s,t) + \dfrac{s+f}{r+f}\theta_1(s,t;f,1)A(s,t)\right.\nonumber\\
&\quad +\left. \dfrac{s+r}{r+f}\theta_1(s,t;r,\alpha)B(s,t)
\right].
\end{align}
\begin{align}
\dfrac{\partial}{\partial s}L_{T}(s|t) & =
-tL_{T}(s;1|t) + u_1(s,t) \left[ \nu_{1}(s,t)\omega_{1}(s,t) + \dfrac{s+f}{r+f}\theta_1(s,t;f,1)A(s,t)\right.\nonumber\\
&\quad +\left. \dfrac{s+r}{r+f}\theta_1(s,t;r,\alpha)B(s,t)
\right].
\end{align}Moreover,
 \begin{align}
\dfrac{\partial}{\partial s}L_{T}(s;n|t) &=
-tL_{T}(s;n+1|t)
+
u_1(s,t)
\left[
\nu_{n+1}(s,t)\omega_{1}(s,t)
+
\dfrac{s+f}{r+f}\theta_1(s,t;f,1)A(s,t)\right. \nonumber\\
&\quad \left.
+
\dfrac{s+r}{r+f}\theta_1(s,t;r,\alpha)B(s,t)
\right].
\end{align}
\begin{align}
\dfrac{\partial}{\partial s}L_{T}(s;n|t) &=
-tL_{T}(s;n+1|t)
+
u_1(s,t)
\left[
\nu_{n+1}(s,t)\omega_{1}(s,t)
+
\dfrac{s+f}{r+f}\theta_1(s,t;f,1)A(s,t)\right. \nonumber\\
&\quad \left.
+
\dfrac{s+r}{r+f}\theta_1(s,t;r,\alpha)B(s,t)
\right].
\end{align} To calculate the higher order partial derivatives of ![]() $L_{T}(s|t)$ we have to use the general Leibniz rule on the second term in (D.15). For this, we have to study the partial derivatives of the factor
$L_{T}(s|t)$ we have to use the general Leibniz rule on the second term in (D.15). For this, we have to study the partial derivatives of the factor ![]() $u(s,t)$, and the functions
$u(s,t)$, and the functions ![]() $A(s,t)$ and
$A(s,t)$ and ![]() $B(s,t)$. We start with
$B(s,t)$. We start with ![]() $u(s,t)$. From (D.13), we observe that
$u(s,t)$. From (D.13), we observe that
 \begin{equation}
h_{r}(s,t)h_{f}(s,t) = C(t)e^{\int\omega_{1}(s,t)ds},
\end{equation}
\begin{equation}
h_{r}(s,t)h_{f}(s,t) = C(t)e^{\int\omega_{1}(s,t)ds},
\end{equation} where ![]() $C(t) := rf\,e^{-t(f+r/\alpha)}$.
$C(t) := rf\,e^{-t(f+r/\alpha)}$.
Consider now t fixed and the two following one-dimensional functions:
 \begin{equation}
g(x(s)) := C(t)e^{\int x(s)ds}, \quad f(y) := \dfrac{y}{(1-y)^{2}}.
\end{equation}
\begin{equation}
g(x(s)) := C(t)e^{\int x(s)ds}, \quad f(y) := \dfrac{y}{(1-y)^{2}}.
\end{equation}Using the functions defined above Eqs. (D.14) and (D.17) can be rewritten as
thus, ![]() $u_{1}(s,t)$ is a nested composite function.
$u_{1}(s,t)$ is a nested composite function.
The derivatives of composite functions can be written using Faà di Bruno’s formula [Reference Faa di Bruno15] as shown in Eq. (D.21):
 \begin{equation}
\dfrac{d^n}{dx^n} f(g(x)) = \sum_{k=1}^{n} f^{(k)}(g(x))\cdot B_{n,k}\Bigr(g'(x),g''(x),\ldots,g^{(n-k+1)}(x)\Bigl),
\end{equation}
\begin{equation}
\dfrac{d^n}{dx^n} f(g(x)) = \sum_{k=1}^{n} f^{(k)}(g(x))\cdot B_{n,k}\Bigr(g'(x),g''(x),\ldots,g^{(n-k+1)}(x)\Bigl),
\end{equation} where ![]() $B_{n,k}$ are the incomplete (or partial) exponential Bell polynomials [Reference Bell9, Reference Mihoubi26] defined below
$B_{n,k}$ are the incomplete (or partial) exponential Bell polynomials [Reference Bell9, Reference Mihoubi26] defined below
 \begin{equation}
B_{n,k}(x_{1},x_{2},\dots ,x_{n-k+1}) =
\sum
\dfrac{n!}{j_{1}!j_{2}!\cdots j_{n-k+1}!}
\left(\dfrac{x_{1}}{1!}\right)^{j_{1}}
\left(\dfrac{x_{2}}{2!}\right)^{j_{2}}
\cdots
\left(\dfrac{x_{n-k+1}}{(n-k+1)!}\right)^{j_{n-k+1}},
\end{equation}
\begin{equation}
B_{n,k}(x_{1},x_{2},\dots ,x_{n-k+1}) =
\sum
\dfrac{n!}{j_{1}!j_{2}!\cdots j_{n-k+1}!}
\left(\dfrac{x_{1}}{1!}\right)^{j_{1}}
\left(\dfrac{x_{2}}{2!}\right)^{j_{2}}
\cdots
\left(\dfrac{x_{n-k+1}}{(n-k+1)!}\right)^{j_{n-k+1}},
\end{equation} where the summation is carried over all sequences ![]() $j_{1},j_{2},j_{3},\ldots,j_{n-k+1}$ of non-negative integers such that conditions below are satisfied
$j_{1},j_{2},j_{3},\ldots,j_{n-k+1}$ of non-negative integers such that conditions below are satisfied
The nth complete exponential Bell polynomial is given by the sum of the incomplete polynomials as:
 \begin{equation}
B_{n}(x_{1},\ldots,x_{n}) =
\sum_{k=1}^{n}B_{n,k}(x_{1},x_{2},\ldots,x_{n-k+1}).
\end{equation}
\begin{equation}
B_{n}(x_{1},\ldots,x_{n}) =
\sum_{k=1}^{n}B_{n,k}(x_{1},x_{2},\ldots,x_{n-k+1}).
\end{equation} The derivatives of composite functions in Eq. (D.21) are similar to the complete exponential Bell polynomials, of which the variables ![]() $x_{1},\ldots,x_{n}$ are replaced by the successive derivatives of the inner function g(x), and the coefficients of the polynomials are factored by the derivatives of the outer function. Since
$x_{1},\ldots,x_{n}$ are replaced by the successive derivatives of the inner function g(x), and the coefficients of the polynomials are factored by the derivatives of the outer function. Since ![]() $u(s,t) = f(g(w_{1}(s,t)))$ is a double composite function, its partial derivatives are given by nested Bell polynomials.
$u(s,t) = f(g(w_{1}(s,t)))$ is a double composite function, its partial derivatives are given by nested Bell polynomials.
From (D.11), we know that the partial derivatives of the innermost function ![]() $\omega_{1}(s,t)$ with respect to s are
$\omega_{1}(s,t)$ with respect to s are
 \begin{equation}
\dfrac{\partial^{n}}{\partial s^{n}}\omega_{1}(s,t) = \omega_{n+1}(s,t).
\end{equation}
\begin{equation}
\dfrac{\partial^{n}}{\partial s^{n}}\omega_{1}(s,t) = \omega_{n+1}(s,t).
\end{equation} The partial derivatives of the first composite function ![]() $g(w_{1}(s,t))$ are calculated using (D.21) where the variable coefficients are the derivatives of
$g(w_{1}(s,t))$ are calculated using (D.21) where the variable coefficients are the derivatives of  $g(x(s)) = C(t)e^{\int x(s)ds}$ evaluated in
$g(x(s)) = C(t)e^{\int x(s)ds}$ evaluated in ![]() $\omega_{1}(s,t)$, and the incomplete Bell polynomials are evaluated on the partial derivatives of
$\omega_{1}(s,t)$, and the incomplete Bell polynomials are evaluated on the partial derivatives of ![]() $\omega_{1}(s,t)$ from Eq. (D.26). The general derivative is given below, we omit the functional dependency on
$\omega_{1}(s,t)$ from Eq. (D.26). The general derivative is given below, we omit the functional dependency on ![]() $\omega_{i}(s,t)$ to keep the notation uncluttered
$\omega_{i}(s,t)$ to keep the notation uncluttered
 \begin{align*}
G_{n}(s,t) :=
\dfrac{\partial^{n}}{\partial s^{n}}
\bigl(h_{r}(s,t)h_{f}(s,t)\bigr) =
h_{r}(s,t)h_{f}(s,t)B_{n}(\omega_{1},\omega_{2},\ldots,\omega_{n}).
\end{align*}
\begin{align*}
G_{n}(s,t) :=
\dfrac{\partial^{n}}{\partial s^{n}}
\bigl(h_{r}(s,t)h_{f}(s,t)\bigr) =
h_{r}(s,t)h_{f}(s,t)B_{n}(\omega_{1},\omega_{2},\ldots,\omega_{n}).
\end{align*} The similarities of the derivatives to the complete Bell polynomials are due to the exponential nature of ![]() $g(x(s))$, which makes the successive derivatives of the outer function self-similar, and hence it can be factored out from the coefficients of the partial polynomials. Notice that derivatives of low order for
$g(x(s))$, which makes the successive derivatives of the outer function self-similar, and hence it can be factored out from the coefficients of the partial polynomials. Notice that derivatives of low order for ![]() $g(x(s))$ may also be easily calculated recursively following from Eq. (D.13).
$g(x(s))$ may also be easily calculated recursively following from Eq. (D.13).
The derivatives of the outermost function f(y) are
 \begin{equation}
\dfrac{d^{n}}{dy^{n}}f(y) =
\dfrac{d^{n}}{dy^{n}}\dfrac{y}{(1-y)^{2}} =
\dfrac{n!}{(1-y)^{2}}\dfrac{y+n}{(1-y)^{n}}.
\end{equation}
\begin{equation}
\dfrac{d^{n}}{dy^{n}}f(y) =
\dfrac{d^{n}}{dy^{n}}\dfrac{y}{(1-y)^{2}} =
\dfrac{n!}{(1-y)^{2}}\dfrac{y+n}{(1-y)^{n}}.
\end{equation} With this we give below the general form of the partial derivatives of ![]() $u(s,t)$ where we drop the functional dependencies of
$u(s,t)$ where we drop the functional dependencies of ![]() $G_{n}(s,t)$ to keep the notation uncluttered
$G_{n}(s,t)$ to keep the notation uncluttered
 \begin{align}
u_{n+1}(s,t)
& := \dfrac{\partial^{n}}{\partial s^{n}} u_1(s,t) \notag \\
& = \sum_{k=1}^{n}
k!\dfrac{(k + h_{r}h_{f})\phantom{^{k+2}} }
{(1 - h_{r}h_{f})^{k+2}}
\cdot B_{n,k}\Bigr(G_{1},G_{2},\ldots,G_{n-k+1}\Bigl), \quad n=1,2,\ldots.
\end{align}
\begin{align}
u_{n+1}(s,t)
& := \dfrac{\partial^{n}}{\partial s^{n}} u_1(s,t) \notag \\
& = \sum_{k=1}^{n}
k!\dfrac{(k + h_{r}h_{f})\phantom{^{k+2}} }
{(1 - h_{r}h_{f})^{k+2}}
\cdot B_{n,k}\Bigr(G_{1},G_{2},\ldots,G_{n-k+1}\Bigl), \quad n=1,2,\ldots.
\end{align} The derivatives of ![]() $A(s,t)$ and
$A(s,t)$ and ![]() $B(s,t)$ are also written in terms of Bell polynomials. This is due to the fact that, from Eq. (D.17) and by definition both functions are composite functions:
$B(s,t)$ are also written in terms of Bell polynomials. This is due to the fact that, from Eq. (D.17) and by definition both functions are composite functions:
 \begin{align*}
A(s,t)
& = \Theta_1(s,t;r,\alpha) + C(t)e^{\int(\Theta_{1}(s,t;f,1) + \Theta_{1}(s,t;r,\alpha))ds}\Theta_1(s,t;f,1), \\
B(s,t)
& = \Theta_1(s,t;f,1) + C(t)e^{\int(\Theta_{1}(s,t;f,1) + \Theta_{1}(s,t;r,\alpha))ds}\Theta_1(s,t;r,\alpha).
\end{align*}
\begin{align*}
A(s,t)
& = \Theta_1(s,t;r,\alpha) + C(t)e^{\int(\Theta_{1}(s,t;f,1) + \Theta_{1}(s,t;r,\alpha))ds}\Theta_1(s,t;f,1), \\
B(s,t)
& = \Theta_1(s,t;f,1) + C(t)e^{\int(\Theta_{1}(s,t;f,1) + \Theta_{1}(s,t;r,\alpha))ds}\Theta_1(s,t;r,\alpha).
\end{align*} Denote by ![]() $\Theta_{1:k}(s,t;a,b)$ the ordered list
$\Theta_{1:k}(s,t;a,b)$ the ordered list ![]() $\Theta_{1}(s,t;a,b),\ldots,\Theta_{k}(s,t;a,b)$. It can be shown by induction that
$\Theta_{1}(s,t;a,b),\ldots,\Theta_{k}(s,t;a,b)$. It can be shown by induction that
 \begin{align}
\dfrac{\partial^{n}}{\partial s^{n}} A(s,t) & =
\Theta_{n+1}(s,t;r,\alpha) +
h_{r}(s,t)h_{f}(s,t)
\sum _{k=0}^{n}{\binom {n}{k}}
B_{n-k+1}\bigl(\Theta_{1:(n-k+1)}(s,t;f,1)\bigr)
B_{k}\bigl(\Theta_{1:k}(s,t;r,\alpha)\bigr),
\end{align}
\begin{align}
\dfrac{\partial^{n}}{\partial s^{n}} A(s,t) & =
\Theta_{n+1}(s,t;r,\alpha) +
h_{r}(s,t)h_{f}(s,t)
\sum _{k=0}^{n}{\binom {n}{k}}
B_{n-k+1}\bigl(\Theta_{1:(n-k+1)}(s,t;f,1)\bigr)
B_{k}\bigl(\Theta_{1:k}(s,t;r,\alpha)\bigr),
\end{align} \begin{align}
\dfrac{\partial^{n}}{\partial s^{n}} B(s,t) & =
\Theta_{n+1}(s,t;f,1) +
h_{r}(s,t)h_{f}(s,t)
\sum _{k=0}^{n}{\binom {n}{k}}
B_{n-k+1}\bigl(\Theta_{1:(n-k+1)}(s,t;r,\alpha)\bigr)
B_{k}\bigl(\Theta_{1:k}(s,t;f,1)\bigr),
\end{align}
\begin{align}
\dfrac{\partial^{n}}{\partial s^{n}} B(s,t) & =
\Theta_{n+1}(s,t;f,1) +
h_{r}(s,t)h_{f}(s,t)
\sum _{k=0}^{n}{\binom {n}{k}}
B_{n-k+1}\bigl(\Theta_{1:(n-k+1)}(s,t;r,\alpha)\bigr)
B_{k}\bigl(\Theta_{1:k}(s,t;f,1)\bigr),
\end{align} where the summations are binomial expansions on the indices of ![]() $\Theta_{k}(s,t;a,b)$, with the first index shifted to the right by one. Getting back to Eq. (D.15), we had that
$\Theta_{k}(s,t;a,b)$, with the first index shifted to the right by one. Getting back to Eq. (D.15), we had that
 \begin{align}
\dfrac{\partial}{\partial s}L_{T}(s|t)& =
-tL_{T}(s;1|t)
+
u_1(s,t)
\left[
\nu_{1}(s,t)\omega_{1}(s,t)
+
\dfrac{s+f}{r+f}\theta_1(s,t;f,1)A(s,t)\right. \nonumber\\
&\quad \left.
+
\dfrac{s+r}{r+f}\theta_1(s,t;r,\alpha)B(s,t)
\right].
\end{align}
\begin{align}
\dfrac{\partial}{\partial s}L_{T}(s|t)& =
-tL_{T}(s;1|t)
+
u_1(s,t)
\left[
\nu_{1}(s,t)\omega_{1}(s,t)
+
\dfrac{s+f}{r+f}\theta_1(s,t;f,1)A(s,t)\right. \nonumber\\
&\quad \left.
+
\dfrac{s+r}{r+f}\theta_1(s,t;r,\alpha)B(s,t)
\right].
\end{align}It can be shown from successive differentiation of Eq. (D.31) and considering (D.16) that the nth partial derivative of the conditioned Laplace transform of the completion time is given as:
 \begin{align}
\dfrac{\partial^{n}}{\partial s^{n}}L_{T}(s|t) &=
(-t)^{n}L_{T}(s;n|t)\nonumber\\
&\quad +
\sum_{k=1}^{n}
(-t)^{n-k}
\dfrac{\partial^{k-1}}{\partial s^{k-1}}
\Biggl(
u_1(s,t)
\left[
\nu_{n-k+1}(s,t)\omega_{1}(s,t)\right.\nonumber\\
&\quad \left. +
A(s,t)\left(\tfrac{s+f}{r+f}\,\theta_1(s,t;f,1)\right)
+
B(s,t)\left(\tfrac{s+r}{r+f}\,\theta_1(s,t;r,\alpha)\right)
\right]
\Biggr),
\end{align}
\begin{align}
\dfrac{\partial^{n}}{\partial s^{n}}L_{T}(s|t) &=
(-t)^{n}L_{T}(s;n|t)\nonumber\\
&\quad +
\sum_{k=1}^{n}
(-t)^{n-k}
\dfrac{\partial^{k-1}}{\partial s^{k-1}}
\Biggl(
u_1(s,t)
\left[
\nu_{n-k+1}(s,t)\omega_{1}(s,t)\right.\nonumber\\
&\quad \left. +
A(s,t)\left(\tfrac{s+f}{r+f}\,\theta_1(s,t;f,1)\right)
+
B(s,t)\left(\tfrac{s+r}{r+f}\,\theta_1(s,t;r,\alpha)\right)
\right]
\Biggr),
\end{align} where the partial derivatives in the right hand side are calculated with the General Leibniz rule, which is given in (D.33) for the product of three functions ![]() $f_{1}(x)$,
$f_{1}(x)$, ![]() $f_{2}(x)$,
$f_{2}(x)$, ![]() $f_{3}(x)$:
$f_{3}(x)$:
 \begin{equation}
\dfrac{d^{n}}{dx^{n}}\left(f_{1}(x)f_{2}(x)f_{3}(x)\right) =
\sum_{k_{1}+k_{2}+k_{3}=n}
\dfrac{n!}{k_{1}!\,k_{2}!\,k_{3}!}
\dfrac{d^{k_{1}}}{dx^{k_{1}}}f_{1}(x)
\dfrac{d^{k_{2}}}{dx^{k_{2}}}f_{2}(x)
\dfrac{d^{k_{3}}}{dx^{k_{3}}}f_{3}(x),
\end{equation}
\begin{equation}
\dfrac{d^{n}}{dx^{n}}\left(f_{1}(x)f_{2}(x)f_{3}(x)\right) =
\sum_{k_{1}+k_{2}+k_{3}=n}
\dfrac{n!}{k_{1}!\,k_{2}!\,k_{3}!}
\dfrac{d^{k_{1}}}{dx^{k_{1}}}f_{1}(x)
\dfrac{d^{k_{2}}}{dx^{k_{2}}}f_{2}(x)
\dfrac{d^{k_{3}}}{dx^{k_{3}}}f_{3}(x),
\end{equation} with the summation extending over all triplets ![]() $(k_{1},k_{2},k_{3})$ of non-negative integers that are such that
$(k_{1},k_{2},k_{3})$ of non-negative integers that are such that  $\displaystyle\sum _{t=1}^{3}k_{t}=n$.
$\displaystyle\sum _{t=1}^{3}k_{t}=n$.
Finally, the mth moment of the completion time T is obtained by unconditioning (D.32) with respect to the task size t whenever the improper integral converges
 \begin{align}
E[T^{m}] & =
(-1)^{m}
\int_{0}^{\infty}
\bigl(\left.\tfrac{\partial^{m}}{\partial s^{m}}L_{T}(s|t)\right|_{s=0}\bigr)
dF_{S}(t)
\notag \\
& =
(-1)^{m}\mu
\int_{0}^{\infty}
\bigl(\left.\tfrac{\partial^{m}}{\partial s^{m}}L_{T}(s|t)\right|_{s=0}\bigr)
e^{-\mu t}dt.
\end{align}
\begin{align}
E[T^{m}] & =
(-1)^{m}
\int_{0}^{\infty}
\bigl(\left.\tfrac{\partial^{m}}{\partial s^{m}}L_{T}(s|t)\right|_{s=0}\bigr)
dF_{S}(t)
\notag \\
& =
(-1)^{m}\mu
\int_{0}^{\infty}
\bigl(\left.\tfrac{\partial^{m}}{\partial s^{m}}L_{T}(s|t)\right|_{s=0}\bigr)
e^{-\mu t}dt.
\end{align} To study the convergence of the integral in (D.34) we look at the asymptotic behavior of the different terms and factors in (D.32) evaluated at s = 0. We will use the definition of asymptotic equivalence given in (D.35). Recall also that we denote ![]() $\Delta = \min\{f,r/\alpha\} \gt 0$ and
$\Delta = \min\{f,r/\alpha\} \gt 0$ and ![]() $\Delta^{+} = f + r/\alpha - \Delta = \max\{f,r/\alpha\} \gt 0$
$\Delta^{+} = f + r/\alpha - \Delta = \max\{f,r/\alpha\} \gt 0$
 \begin{equation}
\psi_{1}(t)\sim\psi_{2}(t) \,\text{if and only if }\, \lim_{t\to\infty}\dfrac{\psi_{1}(t)}{\psi_{2}(t)} = 1.
\end{equation}
\begin{equation}
\psi_{1}(t)\sim\psi_{2}(t) \,\text{if and only if }\, \lim_{t\to\infty}\dfrac{\psi_{1}(t)}{\psi_{2}(t)} = 1.
\end{equation}We classify according to the asymptotic order.
(1) Constant factors:
(a) Main factor of the first term:
 $L_{T}(0;n|t)$
$L_{T}(0;n|t)$
 \begin{equation*}
L_{T}(0;n|t) \sim C_{1}(n) :=
\begin{cases}
1, & \quad f \lt r/\alpha, \\
1/\alpha^{n}, & \quad f \gt r/\alpha, \\
\tfrac{1}{2}(1+1/\alpha^{n}), & \quad f = r/\alpha
\end{cases}, \quad n=0,1,2,\ldots.
\end{equation*}
\begin{equation*}
L_{T}(0;n|t) \sim C_{1}(n) :=
\begin{cases}
1, & \quad f \lt r/\alpha, \\
1/\alpha^{n}, & \quad f \gt r/\alpha, \\
\tfrac{1}{2}(1+1/\alpha^{n}), & \quad f = r/\alpha
\end{cases}, \quad n=0,1,2,\ldots.
\end{equation*}(b) Recurrent factor
 $\Theta_{n}(0,t;a,b)$:
$\Theta_{n}(0,t;a,b)$:
 \begin{align*}
\Theta_{1}(0,t;a,b) & = \dfrac{t}{b}\dfrac{e^{-at/b}}{1-e^{-at/b}}-1/a \sim -1/a, \\
\Theta_{n}(0,t;a,b) & =
(-1)^{n-1}
\left(
\dfrac{t^{n}}{b^{n}}
\sum_{i=1}^{n}W(n,i)
\dfrac{e^{-i\cdot at/b}}{(1-e^{-at/b})^{i}}
-\dfrac{(n-1)!}{a^{n}}
\right) \nonumber\\
&\quad \sim (-1)^{n}\dfrac{(n-1)!}{a^{n}}, \quad n = 2,3,\ldots.
\end{align*}
\begin{align*}
\Theta_{1}(0,t;a,b) & = \dfrac{t}{b}\dfrac{e^{-at/b}}{1-e^{-at/b}}-1/a \sim -1/a, \\
\Theta_{n}(0,t;a,b) & =
(-1)^{n-1}
\left(
\dfrac{t^{n}}{b^{n}}
\sum_{i=1}^{n}W(n,i)
\dfrac{e^{-i\cdot at/b}}{(1-e^{-at/b})^{i}}
-\dfrac{(n-1)!}{a^{n}}
\right) \nonumber\\
&\quad \sim (-1)^{n}\dfrac{(n-1)!}{a^{n}}, \quad n = 2,3,\ldots.
\end{align*}(c) Recurrent factor
 $\omega_{n}(0,t)$:
$\omega_{n}(0,t)$:
 \begin{equation*}
\omega_{n}(0,t) = \Theta_{n}(0,t;f,1) + \Theta_{n}(0,t;r,\alpha)
\sim (-1)^{n}(n-1)!\left(\dfrac{1}{f^{n}}+\dfrac{1}{r^{n}}\right), \quad n = 1,2,\ldots.
\end{equation*}
\begin{equation*}
\omega_{n}(0,t) = \Theta_{n}(0,t;f,1) + \Theta_{n}(0,t;r,\alpha)
\sim (-1)^{n}(n-1)!\left(\dfrac{1}{f^{n}}+\dfrac{1}{r^{n}}\right), \quad n = 1,2,\ldots.
\end{equation*}(d) Recurrent factors
 $A(s,t)$ and
$A(s,t)$ and  $B(s,t)$, and derivatives: from (D.29)–(D.30), and by the continuity of Bell polynomials, we have that for every
$B(s,t)$, and derivatives: from (D.29)–(D.30), and by the continuity of Bell polynomials, we have that for every  $n\geq 0$ there exist constants
$n\geq 0$ there exist constants  $C_{A}(n) \gt 0$ and
$C_{A}(n) \gt 0$ and  $C_{B}(n) \gt 0$ such that
$C_{B}(n) \gt 0$ such that
 \begin{align*}
\dfrac{\partial^{n}}{\partial s^{n}} A(s,t) & \sim (-1)^{n+1}C_{A}(n), \\
\dfrac{\partial^{n}}{\partial s^{n}} B(s,t) & \sim (-1)^{n+1}C_{B}(n).
\end{align*}
\begin{align*}
\dfrac{\partial^{n}}{\partial s^{n}} A(s,t) & \sim (-1)^{n+1}C_{A}(n), \\
\dfrac{\partial^{n}}{\partial s^{n}} B(s,t) & \sim (-1)^{n+1}C_{B}(n).
\end{align*}
(2) Polynomial factors with exponential damping:
(a) Recurrent factor
 $\nu_{n}(0|t)$:
$\nu_{n}(0|t)$:
 \begin{equation*}
\nu_{n}(0|t) \sim e^{-\Delta t}\cdot C_{\nu}(n) :=
e^{-\Delta t}\cdot
\begin{cases}
\tfrac{r}{r+f}, & \quad f \lt r/\alpha, \\
\tfrac{f}{(r+f)}\tfrac{1}{\alpha^{n-1}}, & \quad f \gt r/\alpha, \\
\tfrac{1}{r+f}\left(r+\tfrac{f}{\alpha^{n-1}}\right), & \quad f = r/\alpha
\end{cases},
\quad n = 1,2,\ldots.
\end{equation*}
\begin{equation*}
\nu_{n}(0|t) \sim e^{-\Delta t}\cdot C_{\nu}(n) :=
e^{-\Delta t}\cdot
\begin{cases}
\tfrac{r}{r+f}, & \quad f \lt r/\alpha, \\
\tfrac{f}{(r+f)}\tfrac{1}{\alpha^{n-1}}, & \quad f \gt r/\alpha, \\
\tfrac{1}{r+f}\left(r+\tfrac{f}{\alpha^{n-1}}\right), & \quad f = r/\alpha
\end{cases},
\quad n = 1,2,\ldots.
\end{equation*}(b) Recurrent factors
 $\theta_{k}(0,t;a,b)$ and derivatives of
$\theta_{k}(0,t;a,b)$ and derivatives of  $\theta_1(0,t;a,b)$:
$\theta_1(0,t;a,b)$:
 \begin{equation*}
\theta_{k}(s,t;a,b) \sim e^{-k\cdot at/b},
\end{equation*}
\begin{equation*}
\theta_{k}(s,t;a,b) \sim e^{-k\cdot at/b},
\end{equation*} \begin{equation*}
\left.\frac{\partial^{n}}{\partial s^{n}}\theta_1(s,t;a,b)\right|_{s=0}
= (-1)^{n}\left(\frac{t}{b}\right)^{\!\!n} \sum_{i=1}^{n+1}W(n,i)\theta_{i}(0,t;a,b)
\sim (-1)^{n}\left(\frac{t}{b}\right)^{n}e^{-at/b},
\quad n=1,2,\ldots.
\end{equation*}
\begin{equation*}
\left.\frac{\partial^{n}}{\partial s^{n}}\theta_1(s,t;a,b)\right|_{s=0}
= (-1)^{n}\left(\frac{t}{b}\right)^{\!\!n} \sum_{i=1}^{n+1}W(n,i)\theta_{i}(0,t;a,b)
\sim (-1)^{n}\left(\frac{t}{b}\right)^{n}e^{-at/b},
\quad n=1,2,\ldots.
\end{equation*}(c) Accompanying factors of
 $A(0,t)$ and
$A(0,t)$ and  $B(0,t)$, and derivatives:
$B(0,t)$, and derivatives:
 \begin{equation*}
\left.\dfrac{\partial^{n}}{\partial s^{n}}\left(\frac{s+a}{r+f}\,\theta_1(s,t;a,b)\right)\right|_{s=0}
\sim \dfrac{1}{r+f}\left[n+ a(-1)^{n-1}\dfrac{t^{n-1}}{b^{n-1}}\right]e^{-at/b},
\quad n=1,2,\ldots.
\end{equation*}
\begin{equation*}
\left.\dfrac{\partial^{n}}{\partial s^{n}}\left(\frac{s+a}{r+f}\,\theta_1(s,t;a,b)\right)\right|_{s=0}
\sim \dfrac{1}{r+f}\left[n+ a(-1)^{n-1}\dfrac{t^{n-1}}{b^{n-1}}\right]e^{-at/b},
\quad n=1,2,\ldots.
\end{equation*}
(3) Exponential growth factors: recurrent factor
 $u_{n}(0,t)$.
$u_{n}(0,t)$.Again due to the continuity of the Bell polynomials, for every
 $n\in\mathbb{N}$ there exists a constant
$n\in\mathbb{N}$ there exists a constant  $C_{G}(n) \gt 0$ such that
$C_{G}(n) \gt 0$ such that  $G_{n}(0,t) \sim (-1)^{n}C_{G}(n)$, and since the dominant term in (D.28) is for k = n, there exists a constant
$G_{n}(0,t) \sim (-1)^{n}C_{G}(n)$, and since the dominant term in (D.28) is for k = n, there exists a constant  $C_{B}(n-1) \gt 0$ such that
$C_{B}(n-1) \gt 0$ such that  $\left.B_{n-1,n-1}(G_{1})\right|_{s=0} \sim (-1)^{n-1}C_{B}(n-1)$. From here, given that
$\left.B_{n-1,n-1}(G_{1})\right|_{s=0} \sim (-1)^{n-1}C_{B}(n-1)$. From here, given that
 \begin{equation*}
\dfrac{\bigl(n + h_{r}(0,t)h_{f}(0,t)\bigr)\phantom{^{n+2}}}{\bigl(1 - h_{r}(0,t)h_{f}(0,t)\bigr)^{n+2}}
\sim (n+1)e^{(n+2)\Delta t},
\end{equation*}
\begin{equation*}
\dfrac{\bigl(n + h_{r}(0,t)h_{f}(0,t)\bigr)\phantom{^{n+2}}}{\bigl(1 - h_{r}(0,t)h_{f}(0,t)\bigr)^{n+2}}
\sim (n+1)e^{(n+2)\Delta t},
\end{equation*}we obtain
 \begin{equation*}
u_{n}(0,t) \sim (-1)^{n-1}n!\,C_{B}(n-1)\cdot e^{(n+1)\Delta t}, \quad n=1,2,\ldots.
\end{equation*}
\begin{equation*}
u_{n}(0,t) \sim (-1)^{n-1}n!\,C_{B}(n-1)\cdot e^{(n+1)\Delta t}, \quad n=1,2,\ldots.
\end{equation*}Notice that
 $u_{n}(0,t)$ is the only factor that has an asymptotic behavior that is not decaying nor constant for large t, and also that the asymptotic order increases with n, which is the order of the partial derivative.
$u_{n}(0,t)$ is the only factor that has an asymptotic behavior that is not decaying nor constant for large t, and also that the asymptotic order increases with n, which is the order of the partial derivative.
It is easy to see from the first derivative in Eq. (D.15) that  $\left.\frac{\partial}{\partial s}L_{T}(s|t)\right|_{s=0} \sim -\mathcal{C}e^{\Delta t}$, for some constant
$\left.\frac{\partial}{\partial s}L_{T}(s|t)\right|_{s=0} \sim -\mathcal{C}e^{\Delta t}$, for some constant ![]() $\mathcal{C} \gt 0$, and that the expected completion time
$\mathcal{C} \gt 0$, and that the expected completion time ![]() $E[T]$ only exists when
$E[T]$ only exists when ![]() $\Delta =\min\{f,r/\alpha\} \lt \mu$. For higher order derivatives in Eq. (D.32), we only have to observe the last term in the summation, which will yield the higher order terms overall. Additionally, since the partial derivatives of
$\Delta =\min\{f,r/\alpha\} \lt \mu$. For higher order derivatives in Eq. (D.32), we only have to observe the last term in the summation, which will yield the higher order terms overall. Additionally, since the partial derivatives of ![]() $u_1(s,t)$ dominate the asymptotic behavior, we only have to look at the term coming from the Leibniz rule for which
$u_1(s,t)$ dominate the asymptotic behavior, we only have to look at the term coming from the Leibniz rule for which ![]() $u_1(s,t)$ has the partial derivative of order n − 1 and the remaining factors are not differentiated. Then, for
$u_1(s,t)$ has the partial derivative of order n − 1 and the remaining factors are not differentiated. Then, for ![]() $n\geq1$,
$n\geq1$,
 \begin{align}
&\left.\dfrac{\partial^{n}}{\partial s^{n}}L_{T}(s|t)\right|_{s=0} \sim
u_{n}(0,t)
\left[
\nu_{1}(0,t)\omega_{1}(0,t)
+
A(0,t)\left(\tfrac{f}{r+f}\,\theta_1(0,t;f,1)\right) \right. \nonumber\\
&\quad\left. +
B(0,t)\left(\tfrac{r}{r+f}\,\theta_1(0,t;r,\alpha)\right)
\right]
\sim \mathcal{C}(n)e^{n\Delta t},
\end{align}
\begin{align}
&\left.\dfrac{\partial^{n}}{\partial s^{n}}L_{T}(s|t)\right|_{s=0} \sim
u_{n}(0,t)
\left[
\nu_{1}(0,t)\omega_{1}(0,t)
+
A(0,t)\left(\tfrac{f}{r+f}\,\theta_1(0,t;f,1)\right) \right. \nonumber\\
&\quad\left. +
B(0,t)\left(\tfrac{r}{r+f}\,\theta_1(0,t;r,\alpha)\right)
\right]
\sim \mathcal{C}(n)e^{n\Delta t},
\end{align} where ![]() $\mathcal{C}(n)$ is a constant that depends on n. Then, from (D.34), the mth moment
$\mathcal{C}(n)$ is a constant that depends on n. Then, from (D.34), the mth moment ![]() $E[T^{m}]$ is not finite whenever
$E[T^{m}]$ is not finite whenever ![]() $m\Delta -\mu \geq 0$ which is
$m\Delta -\mu \geq 0$ which is ![]() $m\geq \mu/\Delta = \mu/\min\{f,r/\alpha\} = \varepsilon$, and the completion time distribution is power-tailed [Reference Greiner, Jobmann and Lipsky19], that is, there exists a positive constant c such that
$m\geq \mu/\Delta = \mu/\min\{f,r/\alpha\} = \varepsilon$, and the completion time distribution is power-tailed [Reference Greiner, Jobmann and Lipsky19], that is, there exists a positive constant c such that
 \begin{equation}
\overline{F_{T}(t)} \sim \dfrac{c}{t^{\varepsilon}}.
\end{equation}
\begin{equation}
\overline{F_{T}(t)} \sim \dfrac{c}{t^{\varepsilon}}.
\end{equation}