Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-29T08:45:15.466Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal allocation of a coherent system with statistical dependent subsystems

Published online by Cambridge University Press:  24 September 2021

Bin Lu ,
Jiandong Zhang Open the ORCID record for Jiandong Zhang [Opens in a new window]  and
Rongfang Yan Open the ORCID record for Rongfang Yan [Opens in a new window]
Bin Lu
Affiliation:
College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China. E-mails: lubinnwnum@163.com, jiandong.zhang@hotmail.com Department of Mathematics, Lanzhou Jiaotong University, Lanzhou 730070, China. E-mail: yanrf@nwnu.edu.cn
Jiandong Zhang
Affiliation:
College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China. E-mails: lubinnwnum@163.com, jiandong.zhang@hotmail.com
Rongfang Yan*
Affiliation:
College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China. E-mails: lubinnwnum@163.com, jiandong.zhang@hotmail.com
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper studies the optimal allocation policy of a coherent system with independent heterogeneous components and dependent subsystems, the systems are assumed to consist of two groups of components whose lifetimes follow proportional hazard (PH) or proportional reversed hazard (PRH) models. We investigate the optimal allocation strategy by finding out the number 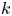$k$ of components coming from Group A in the up-series system. First, some sufficient conditions are provided in the sense of the usual stochastic order to compare the lifetimes of two-parallel–series systems with dependent subsystems, and we obtain the hazard rate and reversed hazard rate orders when two subsystems have independent lifetimes. Second, similar results are also obtained for two-series–parallel systems under certain conditions. Finally, we generalize the corresponding results to parallel–series and series–parallel systems with multiple subsystems in the viewpoint of the minimal path and the minimal cut sets, respectively. Some numerical examples are presented to illustrate the theoretical findings.

Keywords

Coherent systemMajorization orderSchur-concave copulaStochastic orders

Information

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 37 , Issue 1 , January 2023 , pp. 29 - 48
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Barlow, E. & Proschan, F. (1975). Statistical theory of reliability and life testing: Probability models. New York: Holt, Rinehart & Winston.Google Scholar
Belzunce, F. & Martínez-Riquelme, C. (2019). Bounds for the hazard rate and the reversed hazard rate of the convolution of dependent random lifetimes. Journal of Applied Probability 56(4): 1033–1043.CrossRefGoogle Scholar
Belzunce, F., Riquelme, C.M., & Mulero, J. (2016). An introduction to stochastic orders. New York: Academic Press.Google Scholar
Belzunce, F., Martínez-Riquelme, C., & Ruiz, J.M. (2018). Allocation of a relevation in redundancy problems. Applied Stochastic Models in Business and Industry 35(3): 492–503.CrossRefGoogle Scholar
Bhattacharya, D. & Samaniego, F.J. (2008). On the optimal allocation of components within coherent systems. Statistics and Probability Letters 78(7): 938–943.CrossRefGoogle Scholar
Boland, P.J., El-Neweihi, E., & Proschan, F. (1992). Stochastic order for redundancy allocations in series and parallel systems. Advances in Applied Probability 24(1): 161–171.CrossRefGoogle Scholar
Chen, J., Zhang, Y., & Zhao, P. (2019). Comparisons of order statistics from heterogeneous negative binomial variables with applications. Statistics 53(5): 990–1011.CrossRefGoogle Scholar
Collett, D. (1994). Modelling survival data in medical research. London: Chapman & Hall.CrossRefGoogle Scholar
Cox, D.R. (1992). Regression models and life-tables. Springer Series in Statistics. New York: Springer, pp. 527–541.Google Scholar
Cuvelier, E. & Noirhomme-Fraiture, M. (2005). Clayton copula and mixture decomposition. ASMDA 2005, pp. 699–708.Google Scholar
Da, G., Ding, W., & Li, X. (2010). On hazard rate ordering of parallel systems with two independent components. Journal of Statistical Planning and Inference 140(7): 2148–2154.CrossRefGoogle Scholar
Dao, C.D., Zuo, M.J., & Pandey, M. (2014). Selective maintenance for multi-state series–parallel systems under economic dependence. Reliability Engineering & System Safety 121: 240–249.CrossRefGoogle Scholar
Dhaene, J. & Goovaerts, M.J. (1996). Dependency of risks and stop-loss order. ASTIN Bulletin: The Journal of the IAA 26(2): 201–212.CrossRefGoogle Scholar
Dhaene, J. & Goovaerts, M.J. (1997). On the dependency of risks in the individual life model. Insurance: Mathematics and Economics 19(3): 243–253.Google Scholar
Ding, W. & Li, X. (2012). The optimal allocation of active redundancies to $k$-out-of-$n$ systems with respect to hazard rate ordering. Journal of Statistical Planning and Inference 142(7): 1878–1887.CrossRefGoogle Scholar
Ding, W., Fang, R., & Zhao, P. (2019). Reliability analysis of $k$-out-of-$n$ systems based on grouping of components. Advances in Applied Probability 51(2): 339–357.CrossRefGoogle Scholar
Durante, F. & Papini, P.L. (2007). A weakening of Schur-concavity for copulas. Fuzzy Sets and Systems 158(12): 1378–1383.CrossRefGoogle Scholar
Durante, F. & Sempi, C. (2003). Copulae and Schur-concavity. International Mathematical Journal 3: 893–905.Google Scholar
El-Neweihi, E., Proschan, F., & Sethuraman, J. (1986). Optimal allocation of components in parallel–series and series–parallel systems. Journal of Applied Probability 23(3): 770–777.CrossRefGoogle Scholar
Fang, R. & Wang, B. (2020). Stochastic comparisons on sample extremes from independent or dependent gamma samples. Statistics 54(4): 841–855.CrossRefGoogle Scholar
Fang, L., Balakrishnan, N., & Jin, Q. (2020). Optimal grouping of heterogeneous components in series-parallel and parallel-series systems under Archimedean copula dependence. Journal of Computational and Applied Mathematics 377: 112916.CrossRefGoogle Scholar
Feizabadi, M. & Jahromi, A.E. (2017). A new model for reliability optimization of series-parallel systems with non-homogeneous components. Reliability Engineering & System Safety 157: 101–112.CrossRefGoogle Scholar
Guo, Z., Zhang, J., & Yan, R. (2021). On inactivity times of failed components of coherent system under double monitoring. Probability in the Engineering and Informational Sciences, 1–18. doi:10.1017/S0269964821000152.Google Scholar
Gupta, R.C. & Gupta, R.D. (2007). Proportional reversed hazard rate model and its applications. Journal of Statistical Planning and Inference 137(11): 3525–3536.CrossRefGoogle Scholar
Hu, T. & Wang, Y. (2009). Optimal allocation of active redundancies in k-out-of-n systems. Journal of Statistical Planning and Inference 139(10): 3733–3737.CrossRefGoogle Scholar
Jarrahiferiz, J., Kayid, M., & Izadkhah, S. (2019). Stochastic properties of a weighted frailty model. Statistical Papers 60(1): 53–72.CrossRefGoogle Scholar
Kalbfleisch, J.D. & Lawless, J.F. (1989). Inference based on retrospective ascertainment: An analysis of the data on transfusion-related AIDS. Journal of the American Statistical Association 84(406): 360–372.CrossRefGoogle Scholar
Kundu, A., Chowdhury, S., Nanda, A.K., & Hazra, N.K. (2016). Some results on majorization and their applications. Journal of Computational and Applied Mathematics 301: 161–177.CrossRefGoogle Scholar
Kundu, P., Hazra, N.K., & Nanda, A.K. (2020). Reliability study of series and parallel systems of heterogeneous component lifetimes following proportional odds model. Statistics 54(2): 375–401.CrossRefGoogle Scholar
Laniado, H. & Lillo, R.E. (2014). Allocation policies of redundancies in two-parallel-series and two-series-parallel systems. IEEE Transactions on Reliability 63(1): 223–229.CrossRefGoogle Scholar
Lehmann, E.L. (1966). Some concepts of dependence. The Annals of Mathematical Statistics: 1137–1153.CrossRefGoogle Scholar
Li, X. & Ding, W. (2010). Optimal allocation of active redundancies to k-out-of-n systems with heterogeneous components. Journal of Applied Probability 47(1): 254–263.CrossRefGoogle Scholar
Li, X., Yan, R., & Zuo, M.J. (2009). Evaluating a warm standby system with components having proportional hazard rates. Operations Research Letters 37(1): 56–60.CrossRefGoogle Scholar
Ling, X. & Wei, Y. (2020). Optimal allocation of randomly selected redundancies to $k$-out-of-$n$ system with independent but nonidentical components. IEEE Access 8: 88464–88473.CrossRefGoogle Scholar
Ling, X., Wei, Y., & Li, P. (2018). On optimal heterogeneous components grouping in series-parallel and parallel-series systems. Probability in the Engineering and Informational Sciences 33(4): 564–578.CrossRefGoogle Scholar
Majumder, P., Ghosh, S., & Mitra, M. (2020). Ordering results of extreme order statistics from heterogeneous Gompertz–Makeham random variables. Statistics 54(3): 595–617.CrossRefGoogle Scholar
Marshall, A.W., Olkin, I., & Arnold, B.C. (2011). Inequalities: Theory of majorization and its applications. New York: Springer.CrossRefGoogle Scholar
Navarro, J. & Spizzichino, F. (2010). Comparisons of series and parallel systems with components sharing the same copula. Applied Stochastic Models in Business and Industry 26(6): 775–791.CrossRefGoogle Scholar
Nelsen, R.B. (2006). An introduction to copulas. Springer Series in Statistics, Vol. 47. Berlin, Heidelberg: Springer-Verlag.Google Scholar
Shaked, M. & Shanthikumar, G. (2007). Stochastic orders. New York: Springer.CrossRefGoogle Scholar
Singh, H. & Misra, N. (1994). On redundancy allocations in systems. Journal of Applied Probability 31(4): 1004– 1014.CrossRefGoogle Scholar
Sun, M.-X., Li, Y.-F., & Zio, E. (2019). On the optimal redundancy allocation for multi-state series–parallel systems under epistemic uncertainty. Reliability Engineering & System Safety 192: 106019.CrossRefGoogle Scholar
Tavakkoli-Moghaddam, R., Safari, J., & Sassani, F. (2008). Reliability optimization of series-parallel systems with a choice of redundancy strategies using a genetic algorithm. Reliability Engineering and System Safety 93(4): 550–556.CrossRefGoogle Scholar
Torrado, N. (2021). On allocation policies in systems with dependence structure and random selection of components. Journal of Computational and Applied Mathematics 388: 113274.CrossRefGoogle Scholar
Yan, R. & Luo, T. (2018). On the optimal allocation of active redundancies in series system. Communications in Statistics – Theory and Methods 47(10): 2379–2388.CrossRefGoogle Scholar
Yan, R. & Wang, J. (2020). Component level versus system level at active redundancies for coherent systems with dependent heterogeneous components. Communications in Statistics – Theory and Methods, 1–22. doi:10.1080/03610926.2020.1767140.Google Scholar
Yan, R., Da, G., & Zhao, P. (2013). Further results for parallel systems with two heterogeneous exponential components. Statistics 47(5): 1128–1140.CrossRefGoogle Scholar
Yan, R., Lu, B., & Li, X. (2018). On redundancy allocation to series and parallel systems of two components. Communications in Statistics – Theory and Methods 48(18): 4690–4701.CrossRefGoogle Scholar
Yan, R., Zhang, J., & Zhang, Y. (2021). Optimal allocation of relevations in coherent systems. Journal of Applied Probability 58(4): 1–22. In press.CrossRefGoogle Scholar
You, Y., Fang, R., & Li, X. (2016). Allocating active redundancies to $k$-out-of-$n$ reliability systems with permutation monotone component lifetimes. Applied Stochastic Models in Business and Industry 32(5): 607–620.CrossRefGoogle Scholar
Zhang, Y. (2018). Optimal allocation of active redundancies in weighted $k$-out-of-$n$ systems. Statistics and Probability Letters 135: 110–117.CrossRefGoogle Scholar