1 Introduction
Amid growing concerns over the lack of statistical power in most of quantitative political science (Arel-Bundock et al. Reference Arel-Bundock, Briggs, Doucouliagos, Aviña and Stanley2022), one key property in randomized experiments is the precision of the procedure used to estimate treatment effects. Researchers have only one chance to conduct randomization, collect data, and generate an estimate of the average treatment effect (ATE). The stakes are high, so increasing precision of the research design is key to detecting non-zero treatment effects when they exist.
In this letter, we revisit two experimental designs that are promoted as particularly simple and effective ways to enhance precision, but rely on pre-treatment information to do so: (1) block randomized and (2) pre-post designs. We assess these designs for three main reasons. First, the literature explicitly recommends using these designs as particularly effective ways to increase precision. Research shows that blocking is unlikely to hurt (Imai, King, and Stuart Reference Imai, King and Stuart2008) and can greatly improve precision in applied settings (Moore Reference Moore2012). Imai et al. (Reference Imai, King and Stuart2008) advise that when feasible, “blocking on potentially confounding covariates should always be used” (493). Regarding repeated measures designs, recent work recommends researchers to implement this design “whenever possible” to improve precision (Clifford, Sheagley, and Piston Reference Clifford, Sheagley and Piston2021, 1062).
Second, and most importantly, we focus on these designs because the literature’s promise of improved precision assumes sample size is not affected by the decision to implement them. Yet in practice, implementing these designs may decrease sample size since they require researchers collect additional information about units before administering experimental treatments. We highlight two forms of sample loss. First, explicit sample loss happens when a study’s units drop from the experiment under an alternative design when they would not under the standard design. Second, implicit sample loss happens when investing in an alternative design forces the researcher to settle with a smaller sample size, mainly for budgeting reasons. Any sample loss associated with implementing block randomized and pre-post designs makes it unclear how precision is affected, and thus, how researchers should navigate these design decisions.
Third, despite the decisive advice in the literature that block randomized and pre-post designs provide precision gains, they are not widely implemented in experimental political science. We find that these designs were implemented in only 15% (32/217) of a sample of experiments published in the 2022–2023 issues of six political science journals (See Section D of the Supplementary Material for details).Footnote 1
In this letter, we put the theoretical benefits of these alternative designs to the test using real-world data. We replicate three published experiments, randomizing participants to counterfactual designs to explore the consequences of implementing these designs in practice for sample loss, increased precision, and more. Our evidence helps researchers determine whether the investment in these alternative designs is worth it. And more broadly, we hope this letter assists applied researchers in implementing experimental designs that will detect non-zero treatment effects when they exist, particularly when a researcher has a limited budget.
2 Balancing Precision and Retention Under Alternative Design
The most common experimental design implemented in the social sciences has two defining features. First, it assigns treatments using simple or complete randomization. Second, it measures outcomes only after administering treatments. We refer to this design as the “standard” design.
Precision concerns often motivate researchers to entertain alternative research designs. In this letter, we compare precision of the standard design to precision of three other designs whose implementation may introduce sample loss: block randomized designs, pre-post designs, and their combination. This section first explains how these alternative designs improve precision over the standard design in theory, but in practice, this critically depends on their degree of associated sample loss.
2.1 Precision of the Standard Experimental Design
Consider an experiment under the standard experimental design with a sample of N units indexed by
![]() $i = \{1, 2, 3, ..., N\}$
. For simplicity, consider a binary treatment,
$i = \{1, 2, 3, ..., N\}$
. For simplicity, consider a binary treatment,
![]() $Z_i = \{0,1\}$
resulting from either simple or complete random assignment. With a sufficiently large sample size, both randomization procedures yield equivalent treatment assignments in expectation. We focus on complete randomization for the sake of exposition. Using the Neyman–Rubin potential outcomes framework, assume two potential outcomes, one if a unit receives treatment (
$Z_i = \{0,1\}$
resulting from either simple or complete random assignment. With a sufficiently large sample size, both randomization procedures yield equivalent treatment assignments in expectation. We focus on complete randomization for the sake of exposition. Using the Neyman–Rubin potential outcomes framework, assume two potential outcomes, one if a unit receives treatment (
![]() $Y_i(1)$
) and one if the unit receives the control (
$Y_i(1)$
) and one if the unit receives the control (
![]() $Y_i(0)$
). Assume that potential outcomes satisfy SUTVA and excludability, and that treatment is randomly assigned.
$Y_i(0)$
). Assume that potential outcomes satisfy SUTVA and excludability, and that treatment is randomly assigned.
In this letter, we are interested in the ATE estimand, as it is the most common quantity of interest in social science applications:
![]() $ATE = E[Y_i(1) - Y_i(0)].$
We can obtain an unbiased estimate of the ATE by calculating the difference in the average observed outcome in the treatment and control groups:
$ATE = E[Y_i(1) - Y_i(0)].$
We can obtain an unbiased estimate of the ATE by calculating the difference in the average observed outcome in the treatment and control groups:
![]() $\widehat {ATE} = E[Y_i(1) | Z_i = 1] - E[Y_i(0) | Z_i = 0]$
.
$\widehat {ATE} = E[Y_i(1) | Z_i = 1] - E[Y_i(0) | Z_i = 0]$
.
The true (unobserved) standard error of the difference in means estimator (Gerber and Green Reference Gerber and Green2012, 57) under the standard design, assuming half of the participants are assigned to treatment and half to control (
![]() $m=N/2$
), is
$m=N/2$
), is
 $$ \begin{align} SE(\widehat{ATE}_{\text{Standard}}) = \sqrt{\frac{\text{Var}(Y_i(0)) + \text{Var}(Y_i(1)) + 2\text{Cov}(Y_i(0), Y_i(1))}{N-1}}. \end{align} $$
$$ \begin{align} SE(\widehat{ATE}_{\text{Standard}}) = \sqrt{\frac{\text{Var}(Y_i(0)) + \text{Var}(Y_i(1)) + 2\text{Cov}(Y_i(0), Y_i(1))}{N-1}}. \end{align} $$
2.2 Improving
 ${SE}(\widehat {{ATE}})$
with Alternative Designs
${SE}(\widehat {{ATE}})$
with Alternative Designs
The simplest alternative design to improve precision would be to increase the sample size. Because of the factor
![]() $\frac {1}{\sqrt {N-1}}$
in
$\frac {1}{\sqrt {N-1}}$
in
![]() $SE(\widehat {ATE}_{\text {Standard}})$
, to cut the standard error in half under the standard design, a researcher would need four times the sample size. However, it is often cost prohibitive and thus not an option for applied researchers to increase N as a route to meaningfully increase precision. Even if cost is not an issue, not all populations of interest are easily sampled from to increase sample size, as may be the case if conducting a survey experiment with a sample of Black Americans. Likewise, many field experiments cannot increase their sample size for logistical reasons, like recruiting enumerators or visiting locations, even if funds permitted.
$SE(\widehat {ATE}_{\text {Standard}})$
, to cut the standard error in half under the standard design, a researcher would need four times the sample size. However, it is often cost prohibitive and thus not an option for applied researchers to increase N as a route to meaningfully increase precision. Even if cost is not an issue, not all populations of interest are easily sampled from to increase sample size, as may be the case if conducting a survey experiment with a sample of Black Americans. Likewise, many field experiments cannot increase their sample size for logistical reasons, like recruiting enumerators or visiting locations, even if funds permitted.
When increasing N is not an option, we have discussed two design choices—block randomized and pre-post designs—that the literature promotes as particularly simple and effective ways to increase precision. Block randomized and pre-post designs achieve precision gains by reducing the variance in potential outcomes relative to
![]() $Var(Y_i(0))$
and
$Var(Y_i(0))$
and
![]() $Var(Y_i(1))$
of Equation (1). See Appendices A and B for a more detailed demonstration of this point using the standard errors of the block randomized and pre-post designs. In brief, block randomized designs accomplishes this by assigning treatment within subgroups of units that the researcher expects will respond similarly to the experimental interventions, creating mini-experiments where the treatment and control groups’ potential outcomes are as similar as possible. Pre-post designs accomplish this by using pre-treatment measures of the outcome in estimation of treatment effects. These are not the only strategies available to improve statistical precision in experiments, but as Appendices A and B discuss in more detail, they reflect two general reasons why a researcher would invest in collecting pre-treatment information to do so: First, block randomization is more effective when blocking covariates correlate with potential outcomes. Second, pre-post designs are more effective when pre-treatment outcomes correlate with observed post-treatment outcomes.
$Var(Y_i(1))$
of Equation (1). See Appendices A and B for a more detailed demonstration of this point using the standard errors of the block randomized and pre-post designs. In brief, block randomized designs accomplishes this by assigning treatment within subgroups of units that the researcher expects will respond similarly to the experimental interventions, creating mini-experiments where the treatment and control groups’ potential outcomes are as similar as possible. Pre-post designs accomplish this by using pre-treatment measures of the outcome in estimation of treatment effects. These are not the only strategies available to improve statistical precision in experiments, but as Appendices A and B discuss in more detail, they reflect two general reasons why a researcher would invest in collecting pre-treatment information to do so: First, block randomization is more effective when blocking covariates correlate with potential outcomes. Second, pre-post designs are more effective when pre-treatment outcomes correlate with observed post-treatment outcomes.
However, any precision gains are called into question if these designs also inflict precision costs by reducing N, which we turn to next.
2.3 Sample Loss as a Threat to Improving
 $SE(\widehat {ATE})$
in Practice
$SE(\widehat {ATE})$
in Practice
While block randomized and pre-post designs have clear statistical benefits in theory, a study may lose sample size as a result of their implementation, leaving the conditions under which it is advantageous to implement these designs unclear. We next explain how sample size could be attenuated explicitly or implicitly in practice.
First, “explicit sample loss” arises from circumstances where the sample is defined and units that would finish the experiment under the standard design do not finish under an alternative design. For example, this type of sample loss could occur if the researcher adds many covariates to a pre-treatment survey for blocking or repeated measures purposes, increasing survey fatigue and the likelihood participants drop from the study relative to the standard design. An additional concern with explicit sample loss is that it may also induce bias in treatment effect estimates if units drop from the study in ways that correlate with potential outcomes. While we do not find evidence of this form of correlated sample loss in our replications, we illustrate the circumstances under which this may be a problem for treatment effect estimates in Section G of the Supplementary Material.
Second, “implicit sample loss” arises when investing in an alternative design leads the researcher to settle with a smaller sample size before the study is even fielded. In the context of block randomized and pre-post designs, with a set budget a researcher may collect a smaller sample size in order to afford the collection of more information about units pre-treatment. For example, imagine a researcher quoted around USD$1,333 for their initial plan of a five minute, 1,000 respondent survey experiment on Prolific. Adding four extra pre-treatment questions that require one more minute to complete increases the cost to $1,600. To field this alternative design and stay within budget, the researcher would need to reduce the sample size to about 833 respondents.Footnote 2
Designs that collect additional pre-treatment information could have large precision-increasing effects, but is it worth it to collect this information if explicit and implicit sample loss occur?
3 Experimental Evidence of Precision Under Alternative Designs
To assess whether and to what extent alternative experimental designs increase statistical precision even when incurring sample loss, we conducted a preregistered replication of three published experiments.Footnote 3 For each replication, we conducted our own experiment. We randomized whether participants were assigned to the standard design, a pre-post design (with complete randomization), or a pre-post and block randomized design.
3.1 Replication Sample Selection
We followed the framework proposed by Harden, Sokhey, and Wilson (Reference Harden, Sokhey and Wilson2019) for selecting included studies. Our preregistration details each step of this framework, including defining a population, constructing a sample representative of the population, and defining quantities of interest. In short, we define the population as all published, original randomized experiments in political science where the goal of the experiment is a substantive finding. To select experiments from this population, we utilize the data we collected for a hand coding exercise described in Section D of the Supplementary Material. In Section F of the Supplementary Material, we discuss a simulation exercise that randomly samples from this list of published experiments. In this replication, we hope to generalize to the population while maintaining feasibility of the original data collection, so we take a fine-tuned approach to choosing experiments to replicate.
Table 1 lists key features of the three articles we selected. We replicate Dietrich and Hayes (Reference Dietrich and Hayes2023), Bayram and Graham (Reference Bayram and Graham2022), and Tappin and Hewitt (Reference Tappin and Hewitt.2023), which we refer to as DH, BG, and TH, respectively. These experiments cover different subfields and are representative of the distribution of experimental conditions and observations from our population. DH and BG were single-wave studies, like most survey experiments. TH allowed us to assess a multi-wave study where the first wave solely collected pre-treatment covariates, like in many field experiments. Finally, it was not possible to implement a pre-treatment measure of the outcome in the DH replication, as the main outcome was a reaction to the experimental stimuli. Therefore, we used a quasi pre-post measure of the outcome. Taken together, these experiments vary key features that affect precision, allowing our evidence to have some generalizability to the population.
Table 1 Key features of sampled articles.

We also chose these experiments because they have different motivations for balancing precision and sample retention. For DH, one of their hypotheses pertains specifically to how African American constituents respond to rhetoric from members of Congress. Addressing precision concerns via increasing sample size is not always an option in this context, as survey providers often have a limited number of Black or African American respondents. Researchers who are interested in small or hard-to-reach populations therefore have a motivation to design their experiments to increase precision through other means. We chose BG as a standard example of how an experiment can always consider alternative designs with an eye toward increasing precision, and thus their confidence in their conclusions, even when power analyses at the design stage suggest the experiment achieves conventional levels of power. Finally, we replicate TH because of their interest in treatment effect durability, an important concern in experimental political science. To assess durability, precision concerns are amplified since a later post-treatment wave likely features more attrition and decayed treatment effects.
3.2 Experimental Design per Replication
Table 2 outlines how we implemented each design per study. DH and BG were both single-wave survey experiments. DH and BG asked 7–8 survey items in the standard design, and 3 and 4 additional items, respectively, in the alternative designs to collect a pre-treatment measure of the outcome and predictive covariates.Footnote 4 The standard and pre-post design assigned participants to treatment conditions using complete randomization, while the block randomized design assigned treatment within 15 and 6 unique blocks, respectively, based on a predictive covariate and the pre-treatment measure of the outcome. Finally, TH was a 3-wave study. Wave 1 asked 6 demographics in the standard design, and an additional 12 items in order to implement the alternative designs. Wave 2 administered the treatment using complete randomization in the standard and prepost design. For the block-randomized design, we implemented multivariate continuous blocking between Waves 1 and 2 using demographics, predictive covariates, and pre-treatment measures of the outcomes collected in Wave 1 (Moore Reference Moore2012). All studies were survey experiments conducted on CloudResearch Connect. See the preregistration and Section E of the Supplementary Material for implementation details.
Table 2 Implementation of the standard and alternative designs in each replication.
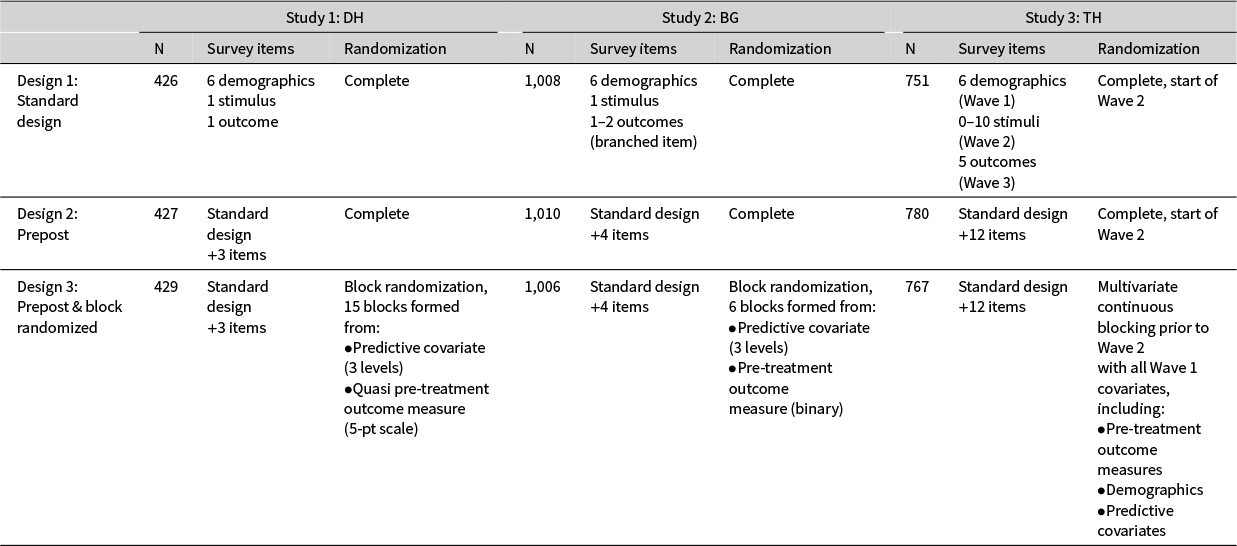
While only a few questions were added to implement the alternative designs, doing so significantly increased survey length (43%, 50%, and 110%, respectively). The alternative designs also added political content pre-treatment. This allows us to asses several concerns that may arise when implementing alternative designs in practice, which we turn to next.
4 Results
4.1 Explicit Sample Loss
First, did alternative designs, requiring longer surveys with more political content, incur greater explicit sample loss? Table E2 in the Supplementary Material shows detailed results. DH and BG—both single-wave studies—featured little explicit sample loss (<1% per design) that was not statistically distinguishable between the standard and alternative designs.
To complete the TH study, respondents had to return to take three survey waves across 1–1.5 weeks. It follows that TH had more explicit sample loss—13.0%, 14.2%, and 20.7% of units dropped at some point in the standard, pre-post, and pre-post with blocking designs, respectively. The block-randomized design featured more explicit loss because we implemented multivariate continuous blocking, utilizing all pre-treatment covariates. The block randomization procedure does not allow missingness in blocking covariates, so we excluded any observation with missingness in these covariates prior to block randomization and treatment randomization. This decision excluded 7% of observations, which explains why this design features more overall sample loss.
In sum, implementing pre-post and/or block randomized designs did not increase the rates of units dropping by their own choice, an encouraging result. However, depending on the researchers’ choices when implementing multivariate continuous blocking in a multi-wave setting, this design may incur additional explicit sample loss. This sample loss is pre-treatment, thus the researcher is not risking biased treatment effect estimation.
4.2 Implicit Sample Loss
Finally, what are the implications for precision when implicit sample loss occurs as a result of implementing an alternative design? We assess this via simulation. We begin with a constant same sample size per study. We then randomly omit observations from the alternative designs to simulate implicit sample loss, re-estimate treatment effects and standard errors, and assess how statistical precision of alternative designs with sample loss compares to the standard design without sample loss. We vary the amount of implicit sample loss from 0% to 50% in increments of 5%. We conduct 1,000 random draws of data per sample size.
Figure 1 visualizes the results. The x-axis shows the hypothetical amount of implicit loss incurred by implementing an alternative design. The y-axis shows the percentage change in the estimated standard error of the alternative design with sample loss relative to the standard design without sample loss. The first panel shows results for DH. Without sample loss, block randomization (dark gray triangles) has slightly more precise estimation than the standard design. At 5% sample loss, the precision afforded by block randomization is no different than the precision afforded by the standard design at full-sample. This suggests there is no harm to precision if implementing block-randomization that requires sacrificing 10% of the sample or less. With 10% sample loss or more, block randomization begins to do worse than the standard design at full sample size.
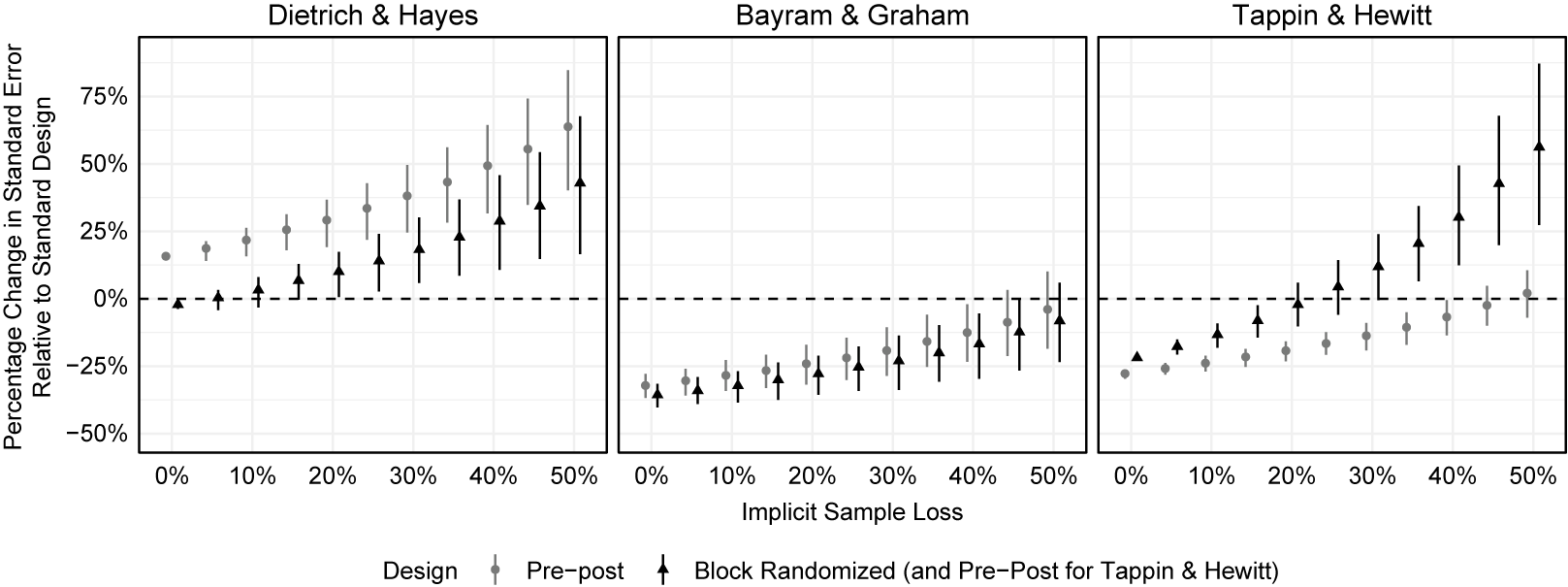
Figure 1 Effects of implicit sample loss on precision.
Note: Figure visualize the effects of implicit sample loss on precision. The x-axis shows the amount of implicit loss incurred by implementing an alternative design, varying the loss from 0% to 50% of the sample. The y-axis shows the percentage change in the estimated standard error of the alternative design with sample loss relative to the standard design without sample loss (with 95% confidence intervals). Results for the prepost and block randomized alternative designs are shown with light gray and dark circles, respectively.
The results are more surprising for the pre-post alternative design. We find that the pre-post design, even with no implicit sample loss, has an approximately 15% larger standard errors than the standard design, and it only grows with sample loss. We believe this occurred for two reasons. First, this replication was the smallest we conducted, with about 430 observations assigned to 8 experimental conditions per design, and the particular treatment effect we preregistered analyzing only has about 210 participants per design. The small sample sizes are likely associated with a large sampling distribution of treatment effect estimates, increasing the probability the three designs are not good counterfactuals for each other. Second, we implemented a quasi pre-treatment measure of the outcome for this design, and it was only weakly correlated with the outcome (r=0.28). The quasi pre-post design, even with a weak correlation, should improve precision relative to the standard design. Nonetheless, the pre-post design was less precise, likely due to sampling variability.
The second panel shows results for BG. Here, pre-post and block randomization provide large precision gains (over 30%) when no sample loss is incurred. In fact, both alternative designs improve precision of the estimated treatment effect, even with a sample size half as large as the standard design. The pre- and post-treatment outcomes feature strong correlation (r=.70), providing sizable precision gains when incorporated. The block randomized design composed blocks with a second pre-treatment covariate; however, using this additional information did not result in precision gains distinguishable from the pre-post design.
The third panel shows results for TH. Again, both pre-post and block randomized designs have sizable increases in precision (25%) relative to the standard design when there is no sample loss. Even at 20% sample loss, block randomization has slightly better precision than the standard design with no loss. Pre-post performs even better in this context. The pre- and post-treatment outcomes feature strong correlation (r=.69). Like with BG, the pre-post design is achieving similar precision with half the sample size as with standard design. If researchers aim to avoid priming participants or must separate pre- and post-treatment measurements for logistical reasons, this replication shows that alternative designs requiring another wave provide precision gains that could withstand sizable sample loss (near 50%).
4.3 Sample Composition
It may be a concern to researchers that implementing an alternative design that requires a lengthy pre-treatment battery may prompt units to drop from the study in a way that alters the sample with which the researcher estimates treatment effects.
We use TH to assess this question since DH and BG had trivially small sample loss and thus no difference in sample composition. We investigate whether an observation being included in the sample or not is differentially predicted across designs by any of the pre-treatment covariates we collected (24 demographic indicators). We find no evidence of a difference between the pre-post design’s sample and the standard design’s sample (Table E3 in the Supplementary Material). We find only one instance where the block randomization with pre-post sample differs from the standard design’s sample. However, our evidence is limited. We can only assess the pre-treatment covariates we observed. Nevertheless, this evidence provides reassurance that sample loss from alternative designs would not result in meaningfully different samples in similar contexts.
4.4 Post-Treatment Attrition
Two forms of post-treatment attrition may pose concerns when implementing an alternative design. First, will alternative designs cause more post-treatment attrition? We fail to find evidence that these rates are different between the alternative designs and the standard design (final column in Table E2 in the Supplementary Material).
Second, will alternative designs cause attrition that differs between treatment and control groups that does not occur in the standard design? This form of attrition is an important concern as it can compromise the estimation of unbiased treatment effects. We can only investigate attrition in the TH replication. Only 4 out of 44 demographic indicators examined had patterns of attrition across treatment arms that differed between the alternative and standard designs (Figure E3 in the Supplementary Material). And in 3 of these cases, the covariate is associated with participants attriting less from the alternative design’s treatment than the standard design’s treatment. Our evidence again comes with the caveat that we can only empirically investigate the characteristics we measured, yet we encouragingly find little evidence of differential post-treatment attrition across alternative designs in this replication exercise.
5 Conclusion
Previous work proposes deviations from the standard experimental design to improve statistical precision under the assumption that sample size is not affected. However, explicit or implicit sample loss are important practical concerns that may be in tension with this advice. Rather than rely on simulation alone or experience gained from fielding many experiments, we bring real-world data to contextualize this advice. In sum, the decision to implement a block randomized and/or pre-post design is context-dependent and should be informed by practical and statistical considerations. We offer high-level guidance for navigating this decision in Section H in the Supplementary Material. The first question to consider is whether pre-treatment information is already available at the level of randomization. If so, researchers can leverage this data to improve statistical precision without concerns about sample loss. If pre-treatment information is unavailable, researchers must assess whether they are adequately powered to detect effects of interest. If sufficiently powered, collecting pre-treatment data may not be necessary and could introduce implicit or explicit sample loss that reduces precision. If not sufficiently powered, collecting pre-treatment information to implement a block randomized and/or pre-post design ought to be considered as these designs may offer precision gains that outweigh even sizeable implicit and explicit sample loss.
We hope this letter assists applied researchers in understanding the extent to which implementing block randomized and/or pre-post designs withstands any possible sample size attenuation that may result in their design. In doing so, we seek to complement a statistical understanding of these designs afforded by textbooks with a practical understanding of how to implement an experiment able to detect true treatment effects.
Acknowledgments
We thank Michelle Dion, Jeff Harden, Geoffrey Sheagley, Natán Skigin, and participants at MPSA 2022 and PolMeth 2022 for helpful feedback. We also thank Amy Brooke Grauley and Shay Hafner for exceptional research assistance.
Funding Statement
This work was supported by the University of Notre Dame.
Competing Interests
The authors declare none.
Data Availability Statement
Replication code for this article is available at Diaz and Rossiter (Reference Diaz and Rossiter2025). A preservation copy of the same code and data can alse be accessed via Dataverse at https://doi.org/10.7910/DVN/LMFOBS.
Ethical Standards
The research involving human subjects was reviewed and approved by the University of Notre Dame Institutional Review Board (Protocol Number: 24-06-8641).
Supplementary Material
For supplementary material accompanying this paper, please visit https://doi.org/10.1017/pan.2025.10008.




