1 Why are some papers cited more than others?
Plenty has been written about word2vec and plenty more will be written in the future.Footnote 1 Given that reality, as well as a severe page limit, there is little hope that I could say much here that hasn’t been said already. My point here is not to praise word2vec or bury it, but to discuss the discussion. Are there lessons to be learned about how to rack up citation counts?
What kinds of papers are massively cited? The definitive last word on a subject? Probably not. The first paper on a subject is more likely to be cited than the last word. That said, while originality is appreciated, the most cited paper is often not the first, or the last, or even the best. Free online availability substantially increases a paper’s impact (Lawrence Reference Lawrence2001; Eysenbach Reference Eysenbach2006). Simplicity and accessibility are preferred over timing and accuracy.
Word2vec is not the first,Footnote 2 last or bestFootnote 3 to discuss vector spaces, embeddings, analogies, similarity metrics, etc. But word2vec is simple and accessible. Anyone can download the codeFootnote 4 and use it in their next paper. Any many do (for better and for worse).
Word2vec often takes on a relatively minor supporting role in these papers, largely bridging the gap between ascii input and an input format that is more appropriate for neural nets; word2vec is not particularly central to the main points of such papers, but nevertheless, in aggregate, the impact of word2vec is ‘huge’ (as Trump likes to say).
The importance of supporting roles should not be overlooked. Supporting roles could well have more impact in aggregate than leading roles. I use the term, supporting role, to include datasets and tools, as well as secondary sources: text books, surveys, discussions of discussions such as this, online courses, videos, etc. Successful supporting roles are richly rewarded with massive citations. Mitch Marcus and Steven Bird, former presidents of the ACL, have both made more than their share of technical contributions to the field, but their top citations, by far, are for supporting roles, datasets and tools such as the Penn Treebank and NLTK, respectively.
Supporting roles are not the first, last or best treatment of a topic, but they are often the most accessible (and the most popular on Google). The rich get richer. . .
2 Promising (if not convincing) initial successes
So you’ve written some code and uploaded it to github. Now, you are hoping the community will download it and cite it, but people aren’t going to put in even the minimal effort required to try it out without motivation to do so. As mentioned in my last column, the hook doesn’t need to be convincing. Promising is sufficient, and actually, promising might be better than convincing. If the hook is too convincing, the community won’t even attempt to contribute improvements.
In word2vec’s case, the hook is the analogy: man is to woman as king is to x. It is impressive that one can just download word2vec and discover that x is queen. Word2vec solves analogy tasks like this by trying all words, x′, in the vocabulary, V, and finding the word that maximizes equation (1).
Words (e.g., king) are represented as vectors (e.g., vec(king)), sequences of K floats, where K is the number of internal dimensions, typically K = 300. Similarity is defined as a cosine
Addition and subtraction of words is expressed in terms of vector addition and vector subtraction. That is, vec(king + woman − man) = vec(king) + vec(woman) − vec(man).
Levy (Reference Levy and Goldberg2014a) suggested that equation (1) can be reformulated in terms of three similarities, as in equation (3). In fact, they prefer equation (4), with small gains reported in Linzen (Reference Linzen2016). We will return to this point in section 3.
There are
![]() ${{4}\atopwithdelims (){2}} = 6$
possible pairwise (symmetric) similarities. I have found it useful to group the six similarities into three types of similarities: vert, hor and diag. Three of the similarities depend on x and three don’t (labeled
${{4}\atopwithdelims (){2}} = 6$
possible pairwise (symmetric) similarities. I have found it useful to group the six similarities into three types of similarities: vert, hor and diag. Three of the similarities depend on x and three don’t (labeled
![]() $\overline{x}$
). There may be opportunities in some cases to infer x similarities from
$\overline{x}$
). There may be opportunities in some cases to infer x similarities from
![]() $\overline{x}$
similarities, especially when the same words show up multiple times on the test, but in different positions.
$\overline{x}$
similarities, especially when the same words show up multiple times on the test, but in different positions.
The intuition for these names comes from expressing the analogy as
While it is pretty amazing that such a simple method does as well as it does, the results are far from too successful, as illustrated in Table 1. Note that just two of the top ten candidates have the correct gender and number (f, sg).Footnote 5 Clearly, there is more work to be done, and plenty of opportunities for the next generation to make improvements.
Table 1. Top ten choices for x in man is to woman as king is to x . Although the top candidate, queen, is an impressive choice, many of the other top ten candidates are less impressive, especially the eight of ten candidates with incorrect gender/number. Candidates with larger hor similarities are more likely to inherit the desired gender and number features from woman. The overall score is close to hor + vert − diag, but not exactly because vector length normalization doesn’t distribute over vector addition and subtraction

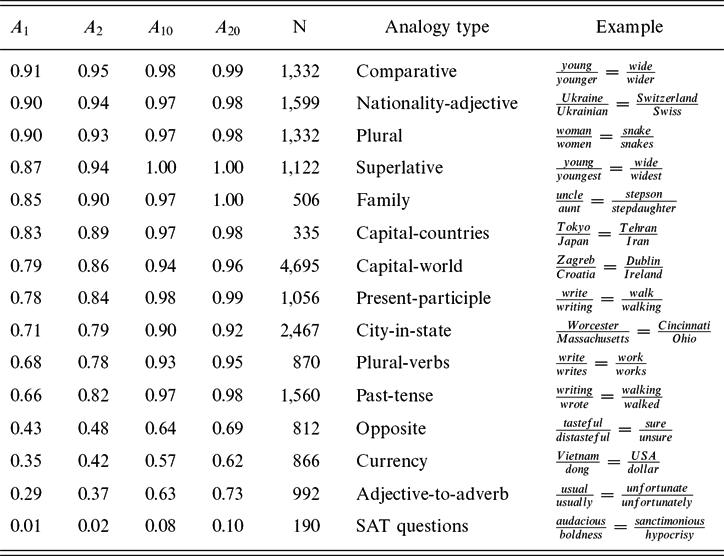
How well does word2vec do? Table 2 reports accuracies on a range of analogy tasks using GoogleNews vectors.Footnote 6 Word2vec works better on some types of analogies than others. Performance is much better on question-words,Footnote 7 the standard test set distributed with the word2vec code, than on real SAT questions.Footnote 8
Table 2. Some types of analogies are easier than others, as indicated by accuracies for top choice (A 1), as well as top 2 (A 2), top 10 (A 10) and top 20 (A 20). The rows are sorted by A 1. These analogies and the type classification come from the questions-words test set, except for the last row, SAT questions. SAT questions are harder than questions-words
3 Error analysis and gaming the test
Given how different questions-words is from real SAT questions, I am concerned that questions-words has become a standard test set in the literature, as observed in Linzen (Reference Linzen2016). Linzen (Reference Linzen2016) then uses this test set to compare equations (3) and (4), and reports that latter is slightly better than the former. While that may well be the case, we need to make sure that such findings can be replicated over more than one test set, especially given the concern in Table 3.Footnote 9
Table 3. The two test sets have very different Venn diagrams. The 178 means that SAT has 178 words that are in a, but not b, c or d. The 14 means that there are 14 words in the overlap between b and d (and not a and c). SAT is more like what I was expecting with small overlaps. Since the vocabulary is much larger than the test set, it is unlikely to find the same word in multiple positions

The task is to predict the last word, d, from the first three: a, b, c. Since the vocabulary (|V| = 300, 000) is much larger than the test set (19,544 four-tuples), it should be unlikely to find the same word in two or more positions. Table 3 shows that this is the case for SAT, but not for questions-words. In fact, every word in questions-words appears in at least two positions. That could not happen by chance.
Once we knew that the test could be gamed, it was pretty straightforward to find a solution. Word2vec doesn’t need to search over |V| = 300, 000 words since no new words show up in the last position that don’t also appear in other positions. Thus, we can search over just 905 = 431 + 399 + 75 words, rather than 300,000. Actually, one can cut down the search space even more by realizing that the mapping from a to b is the same as the mapping from c to d. That is, if one knows that a is Argentina, then b is either Argentinean or peso. And similarly, the same relationship holds between c and d. That is, if we know that c is Argentina, then d is either Argentinean or peso.
It turns out that this mapping is extremely constrained. d is usually (85 per cent) uniquely determined by c. Even when d is ambiguous (as in the case of Argentinean or peso), it isn’t very ambiguous. If we know c, we can almost always (99.6 per cent) limit d down to one or two choices. Given these observations, it isn’t surprising that we could come up with a ‘cheating’ solution that performs incredibly well on the test. My best solution achieved A 1 accuracy of 98.7 per cent.
Obviously, it is rather pointless to game the test, but the fact that it can be done should cast doubt on conclusions in the literature that are based solely on this (questionable) test set. Going forward, it is important to replicate results across a few test sets as in Figure 1. At first, I was looking at just one measure and just one test set (the bottom left plot in Figure 1). Based on that, I jumped to the conclusion that word2vec is stronger for vert (a versus b) than hor (a versus c). But the difference between vert and hor is largely gone in the upper left plot, suggesting that my conclusion was premature; the apparent difference between vert and hor was merely an artifact of the ‘unusual’ properties of the questions-words test set. To support generalizations to a population of interest, it is crucial that the test set be a random sample of that population.

Figure 1. Six boxplots comparing Vert, Hor and Diag. The three columns use three measures of similarity: (1) word2vec distance, (2) domain space and (3) function space. The top row uses SAT questions, and the bottom row uses questions-words. This plot is based on just
![]() $\overline{x}$
similarities, though the plot would not change much if we replaced
$\overline{x}$
similarities, though the plot would not change much if we replaced
![]() $\overline{x}$
similarities with x similarities.
$\overline{x}$
similarities with x similarities.
Figure 1 compares word2vec distances with two additional similarity measures proposed in Turney (Reference Turney2012). All of three similarity measures are related to PMI (Church Reference Church and Hanks1990) in interesting ways,Footnote 10 but domain and function were designed to complement one another. Both follow Firth’s advice, you shall know a word by the company it keeps, but domain does so by looking at nouns in nearby contexts, and function does so by looking at verbs in nearby contexts. The last two plots on the top row show that the difference matters, at least on the SAT test set. Note that domain and function distinguish vert and hor on the top row (but the bottom row is less conclusive, probably because of flaws in questions-words test set).
4 Conclusions
Word2vec has racked up plenty of citations because it satisfies both of Kuhn’s conditions (Kuhn Reference Kuhn2012) for emerging trends: (1) a few initial (promising, if not convincing) successes that motivate early adopters (students) to do more, as well as (2) leaving plenty of room for early adopters to contribute and benefit by doing so. Perhaps, it is a bit of an overstatement to compare word2vec to Kuhn’s scientfic revolutions, but nevertheless, word2vec has had a huge impact on the field. Word2vec is playing an important supporting role. Anyone can download the code and use it in their next paper. Any many do (for better and for worse). The most cited paper is often not the first, or the last, or even the best. Simplicity and accessibility are preferred over timing and accuracy/correctness. The community needs to be careful, however, not to be too convinced by initial promising results. In particular, we need to replicate results over more credible test sets before jumping to premature conclusions.






